
- •1. Определение вектора. Длина вектора. Коллинеарность, компланарность векторов.
- •2. Умножение вектора на число. Свойства операции.
- •3. Сложение векторов, вычитание векторов.
- •4. Базис на плоскости. Теорема о разложении любого вектора по трём базисным векторам.
- •5. Базис в пространстве. Теорема о разложении любого вектора по трем базисным векторам.
- •6. Линейная зависимость векторов.
- •7. Декартова система координат на плоскости и в пространстве, координаты вектора.
- •8. Геометрический смысл координат вектора. Проекция вектора на координатные оси. Направляющие косинусы вектора
- •9. Деление отрезка в данном отношении.
- •6.4. Некоторые приложения скалярного произведения
- •11. Выражение скалярного произведения вектора через координаты сомножителей. Теорема.
- •12. Длина вектора, длина отрезка, угол между векторами, условие перпендикулярности векторов.
- •13. Векторное произведение векторов, его свойства. Площадь параллелограмма.
- •14. Смешанное произведение векторов, его свойства. Условие компланарности вектора. Объем параллелепипеда. Объём пирамиды.
- •15. Способы задания прямой на плоскости.
- •16. Нормальное уравнение прямой на плоскости (вывод). Геометрический смысл коэффициентов.
- •17. Уравнение прямой на плоскости в отрезках (вывод).
- •Приведение общего уравнения плоскости к уравнению плоскости в отрезках.
- •18. Уравнение прямой на плоскости с угловым коэффициентом (вывод).
- •19. Уравнение прямой на плоскости, проходящей через две точки (вывод).
- •20. Угол между прямыми на плоскости (вывод).
- •21. Расстояние от точки до прямой на плоскости (вывод).
- •22. Условия параллельности и перпендикулярности прямых на плоскости (вывод).
- •23. Уравнение плоскости. Нормальное уравнение плоскости (вывод). Геометрический смысл коэффициентов.
- •24. Уравнение плоскости в отрезках (вывод).
- •25. Уравнение плоскости, проходящей через три точки (вывод).
- •26. Угол между плоскостями (вывод).
- •27. Расстояние от точки до плоскости (вывод).
- •28. Условия параллельности и перпендикулярности плоскостей (вывод).
- •29. Уравнения прямой в r3. Уравнения прямой, проходящей через две фиксированные точки (вывод).
- •30. Канонические уравнения прямой в пространстве (вывод).
- •Составление канонических уравнений прямой в пространстве.
- •Частные случаи канонических уравнений прямой в пространстве.
- •Канонические уравнения прямой проходящей через две заданные точки пространства.
- •Переход от канонических уравнений прямой в пространстве к другим видам уравнений прямой.
- •31. Угол между прямыми (вывод).
- •32. Расстояние от точки до прямой на плоскости (вывод).
- •Расстояние от точки до прямой на плоскости – теория, примеры, решения.
- •Первый способ нахождения расстояния от заданной точки до заданной прямой на плоскости.
- •Второй способ, позволяющий найти расстояние от заданной точки до заданной прямой на плоскости.
- •Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости.
- •Расстояние от точки до прямой в пространстве – теория, примеры, решения.
- •Первый способ нахождения расстояния от точки до прямойaв пространстве.
- •Второй способ, позволяющий находить расстояние от точки до прямойaв пространстве.
- •33. Условия параллельности и перпендикулярности прямых в пространстве.
- •34. Взаимное расположение прямых в пространстве и прямой с плоскостью.
- •35. Классическое уравнение эллипса (вывод) и его построение. Каноническое уравнение эллипса имеет вид , где– положительные действительные числа, причём.Как построить эллипс?
- •36. Классическое уравнение гиперболы (вывод) и его построение. Асимптоты.
- •37. Каноническое уравнение параболы (вывод) и построение.
- •38. Функция. Основные определения. Графики основных элементарных функций.
- •39. Числовые последовательности. Предел числовой последовательности.
- •40. Бесконечно малые и бесконечно большие величины. Теорема о связи между ними, свойства.
- •41. Теоремы о действиях над переменными величинами, имеющими конечные пределы.
- •42. Число e.
- •Содержание
- •Способы определения
- •Свойства
- •История
- •Приближения
- •43. Определение предела функции. Раскрытие неопределённостей.
- •44. Замечательные пределы, их вывод. Эквивалентные бесконечно малые величины.
- •Содержание
- •Первый замечательный предел
- •Второй замечательный предел
- •45. Односторонние пределы. Непрерывность и разрывы функции. Односторонние пределы
- •Левый и правый пределы функции
- •Точка разрыва первого рода
- •Точка разрыва второго рода
- •Точка устранимого разрыва
- •46. Определение производной. Геометрический смысл, механический смысл производной. Уравнения касательной и нормали к кривой и точке.
- •47. Теоремы о производной обратной, сложной функций.
- •48. Производные простейших элементарных функций.
- •49. Дифференцирование параметрических, неявных и степенно-показательных функций.
- •21. Дифференцирование неявных и параметрически заданных функций
- •21.1. Неявно заданная функция
- •21.2. Функция, заданная параметрически
- •50. Производные высших порядков. Формула Тейлора.
- •51. Дифференциал. Применение дифференциала к приближенным вычислениям.
- •52. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.
- •53. Теорема о необходимом и достаточном условиях монотонности функции.
- •54. Определение максимума, минимума функции. Теоремы о необходимом и достаточном условиях существования экстремума функции.
- •Теорема (необходимое условие экстремума)
- •55. Выпуклость и вогнутость кривых. Точки перегиба. Теоремы о необходимом и достаточном условиях существования точек перегиба.
- •Доказательство
- •57. Определители n-ого порядка, их свойства.
- •58. Матрицы и действия над ними. Ранг матрицы.
- •Определение
- •Связанные определения
- •Свойства
- •Линейное преобразование и ранг матрицы
- •59. Обратная матрица. Теорема о существовании обратной матрицы.
- •60. Системы линейных уравнений. Матричное решение систем линейных уравнений. Правило Крамера. Метод Гаусса. Теорема Кронекера-Капелли.
- •Решение систем линейных алгебраических уравнений, методы решения, примеры.
- •Определения, понятия, обозначения.
- •Решение элементарных систем линейных алгебраических уравнений.
- •Решение систем линейных уравнений методом Крамера.
- •Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
- •Решение систем линейных уравнений методом Гаусса.
- •Решение систем линейных алгебраических уравнений общего вида.
- •Теорема Кронекера – Капелли.
- •Метод Гаусса для решения систем линейных алгебраических уравнений общего вида.
- •Запись общего решения однородных и неоднородных систем линейных алгебраических с помощью векторов фундаментальной системы решений.
- •Решение систем уравнений, сводящихся к слау.
- •Примеры задач, сводящихся к решению систем линейных алгебраических уравнений.
54. Определение максимума, минимума функции. Теоремы о необходимом и достаточном условиях существования экстремума функции.
Экстремумом
функцииназывается максимальное
(минимальное) значение функции на
заданном множестве. Точка, в которой
достигается экстремум называетсяточкой
экстремума.
Точка![]() называется
точкойлокального максимума функции
называется
точкойлокального максимума функции![]() ,
если выполняется условие:
,
если выполняется условие:![]()
![]()
![]() Аналогично
точка
Аналогично
точка![]() называется
точкойлокального минимума функции
называется
точкойлокального минимума функции![]() ,
если выполняется условие:
,
если выполняется условие:![]()
![]()
![]()
Точки, в которых производнаяравна нулю, называютсястационарными точками. Точки, в которых функциянепрерывна, а её производная либо равна нулю, либо не существует, называютсякритическимиточками.
Теорема (необходимое условие экстремума)
Если
точка
![]() —
точка экстремума функции
—
точка экстремума функции![]() ,
то она критическая.
,
то она критическая.
Доказательство
По
условию точка
![]() —
точка экстремума функции
—
точка экстремума функции![]()
![]() по
теореме Фермапроизводная
по
теореме Фермапроизводная![]()
![]() точка
точка![]() является
критической.
является
критической.
Пример:
Найти
экстремум функции
![]()
![]() .
Найдем
производную этой функции:
.
Найдем
производную этой функции:![]()
![]() критические
точки задаются уравнением
критические
точки задаются уравнением![]() .
Корни этого уравнения
.
Корни этого уравнения![]() и
и![]() .
.
Как
видно по рисунку функция имеет максимум
в точке 1, а минимум в точке 3.
Подставим
эти значения чтобы убедиться в исходную
функцию:
![]()
![]() и
и![]()
![]() в
точке
в
точке![]() функция
имеет минимум, равный -4, а в точке
функция
имеет минимум, равный -4, а в точке![]() функция
имеет максимум, равный 0.
функция
имеет максимум, равный 0.
Замечания:
Не всякая критическая точка является точкой экстремума.
Пример:
Рассмотрим
функцию
![]() .
Построим график этой функции:
.
Построим график этой функции:
Производная
данной функции в точке
![]()
![]()
![]()
![]() по
определению является критической
точкой, однако в этой точке функция не
имеет экстремума.
по
определению является критической
точкой, однако в этой точке функция не
имеет экстремума.
Теорема (первое достаточное условие экстремума в терминах первой производной)
Пусть
функция
![]() определена
идифференцируемав некоторой окрестности точки
определена
идифференцируемав некоторой окрестности точки![]() ,
кроме, быть может, самой точки
,
кроме, быть может, самой точки![]() и
непрерывна в этой точке. Тогда:
и
непрерывна в этой точке. Тогда:
Если производная
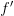 меняет
знак с «-» на «+» при переходе через
точку
меняет
знак с «-» на «+» при переходе через
точку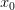 :
: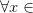
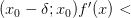
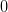 и
и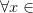
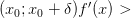
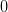 ,
то
,
то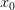 —
точка строго минимума функции
—
точка строго минимума функции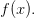
Если производная
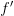 меняет
знак с «+» на «-» при переходе через
точку
меняет
знак с «+» на «-» при переходе через
точку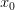 :
: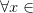
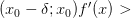
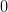 и
и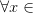
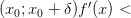
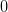 ,
то
,
то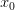 —
точка строго максимума функции
—
точка строго максимума функции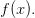
Доказательство
Пусть,
например,
![]() меняет
знак с «-» на «+». Рассмотрим точку
меняет
знак с «-» на «+». Рассмотрим точку![]() на
сегменте
на
сегменте![]() Воспользуемся
теоремой о конечных приращениях Лагранжа:
Воспользуемся
теоремой о конечных приращениях Лагранжа:![]()
![]() ,
,![]() .
Поскольку при переходе через точку
.
Поскольку при переходе через точку![]() функция
меняет знак с «-» на «+», то
функция
меняет знак с «-» на «+», то![]() и
и![]() ,
то
,
то![]()
![]() Аналогично
рассмотрим сегмент
Аналогично
рассмотрим сегмент![]() ,
получим
,
получим![]()
![]()
![]()
![]()
![]() —
точка строгого минимума функции.
—
точка строгого минимума функции.
Замечания:
Если
![]() —
точка строго экстремума, то из этого не
следует, что производная
—
точка строго экстремума, то из этого не
следует, что производная![]() меняет
знак при переходе через точку
меняет
знак при переходе через точку![]()
Теорема (второе достаточное условие строгого экстремума в терминах второй производной)
Пусть
дана функция
![]() ,
она определена в некоторой окрестности
точки
,
она определена в некоторой окрестности
точки![]() , ее
перваяпроизводная
, ее
перваяпроизводная![]() и
пусть
и
пусть![]() ,
тогда:
,
тогда:
Если
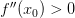 ,
то точка
,
то точка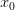 —
точка строгого минимума;
—
точка строгого минимума;Если
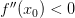 ,
то точка
,
то точка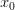 —
точка строгого максимума.
—
точка строгого максимума.
Доказательство
Докажем
теорему для первого случая, когда
![]() .
По скольку
.
По скольку![]() непрерывна,
то на достаточно малом интервале
непрерывна,
то на достаточно малом интервале![]() ,
т.к
,
т.к![]() ,
то
,
то![]() возрастает
в этом интервале.
возрастает
в этом интервале.![]() ,
значит
,
значит![]() на
интервале
на
интервале![]() и
и![]() на
интервале
на
интервале![]() .
Таким
образом функция
.
Таким
образом функция![]() убывает
на интервале
убывает
на интервале![]() и
возрастает на интервале
и
возрастает на интервале![]()
![]() по
первому достаточному условию экстремума
функция в точке
по
первому достаточному условию экстремума
функция в точке![]() имеет
минимум.
Аналогично доказывается
второй случай теоремы.
имеет
минимум.
Аналогично доказывается
второй случай теоремы.
Замечания:
Если
![]() и
и![]() ,
то функция
,
то функция![]() может
и не иметь экстремум в точке
может
и не иметь экстремум в точке![]()
Теорема (третье достаточное условие строгого экстремума в терминах производных порядка больше двух)
Пусть
функция
![]() определена
в некоторой окрестности точки
определена
в некоторой окрестности точки![]() ,
и в этой точке существуют производные
до n-го порядка пусть
,
и в этой точке существуют производные
до n-го порядка пусть![]() ,
,![]() и
и![]()
![]() ,
,![]() Тогда:
Тогда:
Если
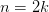 (т.е
(т.е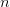 —
четное), то
—
четное), то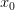 —
точка экстремума:
—
точка экстремума:
если
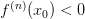 ,
то
,
то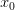 —
точка локального максимума;
—
точка локального максимума;если
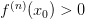 ,
то
,
то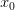 —
точка локального минимума;
—
точка локального минимума;
Если
![]() (т.е
(т.е![]() —
нечетное), то
—
нечетное), то![]() —
не является точкой экстремума.
—
не является точкой экстремума.
Доказательство
Воспользуемся
формулой Тейлора в окрестности точки
![]() с
остатком в форме Пеано:
с
остатком в форме Пеано:![]()
![]()
![]()
![]()
![]() .
По
скольку все производные до
.
По
скольку все производные до![]() порядка
включительно равны нулю получим:
порядка
включительно равны нулю получим:![]()
![]()
![]() Запишем
полученное выражение в виде:
Запишем
полученное выражение в виде:![]()
![]()
![]() .
Выражение
.
Выражение![]() .
Пусть
.
Пусть![]()
![]()
![]() ,
,![]()
![]() .
Отсюда следует, что сохранение или
изменение знака приращения функции во
время перехода через точку
.
Отсюда следует, что сохранение или
изменение знака приращения функции во
время перехода через точку![]() зависит
от четности
зависит
от четности![]() .
Последний факт и доказывает теорему.
.
Последний факт и доказывает теорему.
Определение.
Точка x0 называется точкой
минимума функции f, если для всех x из
некоторой окрестности x0
выполняется неравенство f(x) ≥ f(x0.
Это наглядно показано на рисунке
1: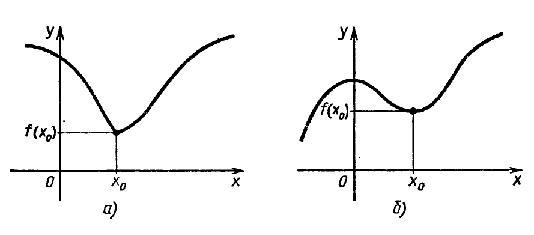 рисунок
1
Определение.Точка x0
называется точкой максимума функции
f, если для всех x из некоторой окрестности
x0 выполняется неравенство
f(x) ≤ f(x0.
Это наглядно
показано на рисунке 2:
рисунок
1
Определение.Точка x0
называется точкой максимума функции
f, если для всех x из некоторой окрестности
x0 выполняется неравенство
f(x) ≤ f(x0.
Это наглядно
показано на рисунке 2: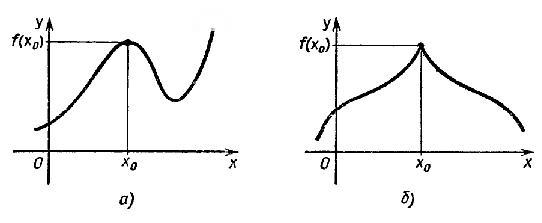 рисунок
2
По определению значение функции
f в точке x0является наибольшим
среди значений функции в окрестности
этой точки, поэтому график функции в
окрестности x0имеет обычно либо
вид гладкого холма, либо вид острого
пика (рис. 1 а) и б) соответственно).
В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б) соответственно).
Другие примеры поведения графиков
функций в точках максимума и минимума
приведены на рисунке ниже:
рисунок
2
По определению значение функции
f в точке x0является наибольшим
среди значений функции в окрестности
этой точки, поэтому график функции в
окрестности x0имеет обычно либо
вид гладкого холма, либо вид острого
пика (рис. 1 а) и б) соответственно).
В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б) соответственно).
Другие примеры поведения графиков
функций в точках максимума и минимума
приведены на рисунке ниже: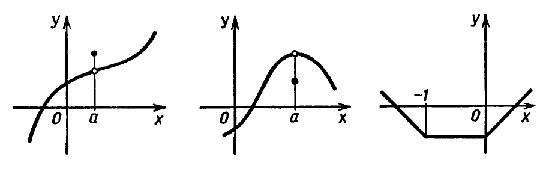 Слева
направо: a - точка максимума; a - точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума.
Для точек минимума
и максимума функции есть общее определение
-точки экстремума. Значение функции
в этих точках соответственно назыветсямаксимумом или минимумом этой функции.
Общее название -экстремум функции.
Точки максимума обычно обозначают xmax,
а точки минимума - xmin.
Слева
направо: a - точка максимума; a - точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума.
Для точек минимума
и максимума функции есть общее определение
-точки экстремума. Значение функции
в этих точках соответственно назыветсямаксимумом или минимумом этой функции.
Общее название -экстремум функции.
Точки максимума обычно обозначают xmax,
а точки минимума - xmin.
