45. Односторонние пределы. Непрерывность и разрывы функции. Односторонние пределы

Определение

Односторонний предел— предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.

Левый и правый пределы функции

Определение

Число называетсяправым пределом функциив точке, если длятакое, что для любогои, выполняется неравенство(рис. 1). Правый предел обозначается

Число называетсялевым пределом функциив точке, если длятакое, что для любогои, выполняется неравенство(рис. 2). Левый предел обозначается

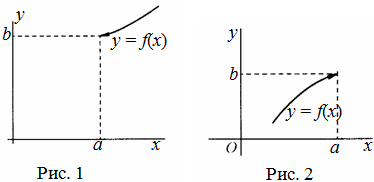
Левый и правый пределы функции называются односторонними пределами.

Теорема

Если существуют и, причем, то существует и. Обратное утверждение также верно.

В случае, если , то пределне существует.

Точка , в которой нарушено хотя бы одно из трех условийнепрерывности функции, а именно:

1. функция 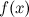определена в точке и ее окрестности;

2. существует конечный предел функции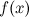в точке;

3. это предел равен значению функции в точке , т.е.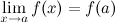

называется точкой разрыва функции.

Пример

Функция не определена в точке, а значит, эта точка является точкой разрыва указанной функции.

Точка разрыва первого рода

Определение

Если в точке существуют конечные пределыи, такие, что, то точканазываетсяточкой разрыва первого рода.

Пример

Функция 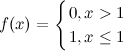в точкеимеет разрыв первого рода, так как

, а

Точка разрыва второго рода

Определение

Если хотя б один из пределов илине существует или равен бесконечности, то точканазываетсяточкой разрыва второго рода.

Пример

Для функции точка- точка разрыва второго рода, так как.

Точка устранимого разрыва

Определение

Если существуют левый и правый пределы функциив точке и они равны друг другу, но не совпадают со значением функциив точке:или функцияне определена в точке, то точканазываетсяточкой устранимого разрыва.

Пример

Рассмотрим функцию 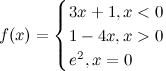. Найдемодносторонние пределыи значение функции в точке:

Так как и не равны значению функции в точке, то точка- точка устранимого разрыва.

46. Определение производной. Геометрический смысл, механический смысл производной. Уравнения касательной и нормали к кривой и точке.

Пусть функция у = f(x) определена на некотором интервале (а; b). Проделаем следующие операции:

- аргументу х (а; b) дадим приращение ∆х: (х + ∆х)(а; b);

- найдем соответствующее приращение функции: ∆у = f(x+∆x) - f(х);

- составим отношение приращения функции к приращению аргумента: ;

- найдем предел этого отношения при ∆х → 0:

Если этот предел существует, то его называют производной функции f(x) и обозначают одним из символов ;f'(x); у'; ;.

Производной функции у = f(x) в точке x₀ называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Итак, по определению

y′ = илиf′(x₀) =.

Функция у = f(х), имеющая производную в каждой точке интервала (а; b), называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.

Значение производной функции у = f(х) в точке х = x₀ обозначается одним из символов: илиy'(x₀).

Пусть материальная точка (некоторое тело) М движется неравномер­но по некоторой прямой. Каждому значению времени t соответствует опре­деленное расстояние ОМ = S до некоторой фиксированной точки О. Это расстояние зависит от истекшего времени t, т. е. S = S(t).

Это равенство называют законом движения точки. Требуется найти скорость движения точки.

Если в некоторый момент времени t точка занима­ет положение M, то в момент времени t + ∆ t (∆t — приращение времени) точка займет положение M₁, где ОМ₁ = S + ∆S (∆S — приращение расстояния) (см. рис. 1). Таким образом, перемещение точки М за время ∆t будет ∆S = S(t + ∆t) – S(t).

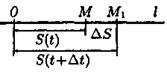
Рис. 1.

Отношение выражает среднюю скоростьдвижения точки за вре­мя∆t:

V_ср.= .

Средняя скорость зависит от значения ∆t: чем меньше ∆t, тем точнее средняя скорость выражает скорость движения точки в данный момент времени t.

Предел средней скорости движения при стремлении к нулю промежут­ка времени ∆t называется скоростью движения точки в данный момент времени(или мгновенной скоростью). Обозначив эту скорость через V,получим

, или . (7.4)

 

Если функция y=f(x) описывает какой-либо физический процесс, то производная есть скорость протекания этого процесса.

Возьмем на непрерывной кривой L две точки М и М₁(см. рис. 2).

Прямую MM₁, проходящую через эти точки, называют секущей.

Пусть точка М₁, двигаясь вдоль кривой L, неограниченно приближа­ется к точке М. Тогда секущая, поворачиваясь около точки М, стремится к некоторому предельному положению МТ.

Касательной к данной кривой в данной точке М называется предельное положение МТ секущей MM₁, проходящей через точку М, ко­гда вторая точка пересечения М₁ неограниченно приближается по кривой к точке М.

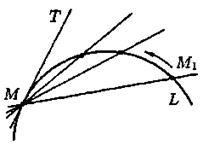
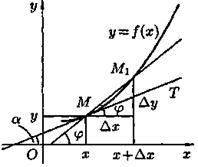
Рис. 2. Рис. 3.

 

Рассмотрим график непрерывной кривой у = f(x), имеющий в точке

М(x; у)невертикальную касательную. Найдем ее угловой коэффи­циент k= tg α,где α — угол касательной с осью Ох.

Для этого проведем через точку М и точку М₁графика с абсциссой х + ∆x; секущую (см. рис. 3). Обозначим через φ — угол между секущей МM₁ и осью Ох. На рисунке видно, что угловой коэффициент секущей

k_сек.=tg φ==.

При ∆x → 0 в силу непрерывности функции приращение ∆у тоже стре­мится к нулю; поэтому точка M₁ неограниченно приближается по кривой к точке М, а секущая ММ₁, поворачиваясь около точки М, переходит в касательную. Угол φ → α, т. е. .

Следовательно,

Поэтому угловой коэффициент касательной равен

k = tg α = ==. (7.5)

Следовательно, угловой коэффициент касательной , то есть производнаяв точкеравна угловому коэффициенту касательной к графику функциив точке, абсцисса которой равна. В этом заключается геометрический смысл производной.

Если точка касания имеет координаты(рис.4), то угловой коэффициент касательной есть. Пользуясь уравнением прямой, проходящей через заданную точку в заданном направлении, можно записать уравнения касательной:.

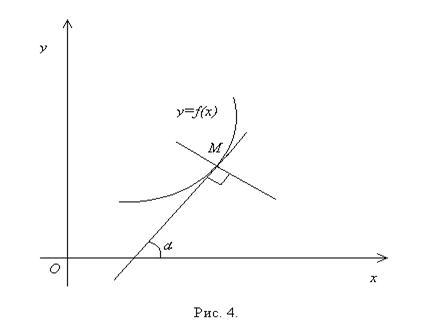
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.

Так как нормаль перпендикулярна касательной, то ее угловой коэффициент

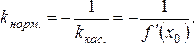
Поэтому уравнение нормали имеет вид 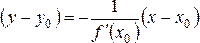(если).

Теорема. Если функция дифференцируема в некоторой точке, то она непрерывна в ней.