
- •1. Определение вектора. Длина вектора. Коллинеарность, компланарность векторов.
- •2. Умножение вектора на число. Свойства операции.
- •3. Сложение векторов, вычитание векторов.
- •4. Базис на плоскости. Теорема о разложении любого вектора по трём базисным векторам.
- •5. Базис в пространстве. Теорема о разложении любого вектора по трем базисным векторам.
- •6. Линейная зависимость векторов.
- •7. Декартова система координат на плоскости и в пространстве, координаты вектора.
- •8. Геометрический смысл координат вектора. Проекция вектора на координатные оси. Направляющие косинусы вектора
- •9. Деление отрезка в данном отношении.
- •6.4. Некоторые приложения скалярного произведения
- •11. Выражение скалярного произведения вектора через координаты сомножителей. Теорема.
- •12. Длина вектора, длина отрезка, угол между векторами, условие перпендикулярности векторов.
- •13. Векторное произведение векторов, его свойства. Площадь параллелограмма.
- •14. Смешанное произведение векторов, его свойства. Условие компланарности вектора. Объем параллелепипеда. Объём пирамиды.
- •15. Способы задания прямой на плоскости.
- •16. Нормальное уравнение прямой на плоскости (вывод). Геометрический смысл коэффициентов.
- •17. Уравнение прямой на плоскости в отрезках (вывод).
- •Приведение общего уравнения плоскости к уравнению плоскости в отрезках.
- •18. Уравнение прямой на плоскости с угловым коэффициентом (вывод).
- •19. Уравнение прямой на плоскости, проходящей через две точки (вывод).
- •20. Угол между прямыми на плоскости (вывод).
- •21. Расстояние от точки до прямой на плоскости (вывод).
- •22. Условия параллельности и перпендикулярности прямых на плоскости (вывод).
- •23. Уравнение плоскости. Нормальное уравнение плоскости (вывод). Геометрический смысл коэффициентов.
- •24. Уравнение плоскости в отрезках (вывод).
- •25. Уравнение плоскости, проходящей через три точки (вывод).
- •26. Угол между плоскостями (вывод).
- •27. Расстояние от точки до плоскости (вывод).
- •28. Условия параллельности и перпендикулярности плоскостей (вывод).
- •29. Уравнения прямой в r3. Уравнения прямой, проходящей через две фиксированные точки (вывод).
- •30. Канонические уравнения прямой в пространстве (вывод).
- •Составление канонических уравнений прямой в пространстве.
- •Частные случаи канонических уравнений прямой в пространстве.
- •Канонические уравнения прямой проходящей через две заданные точки пространства.
- •Переход от канонических уравнений прямой в пространстве к другим видам уравнений прямой.
- •31. Угол между прямыми (вывод).
- •32. Расстояние от точки до прямой на плоскости (вывод).
- •Расстояние от точки до прямой на плоскости – теория, примеры, решения.
- •Первый способ нахождения расстояния от заданной точки до заданной прямой на плоскости.
- •Второй способ, позволяющий найти расстояние от заданной точки до заданной прямой на плоскости.
- •Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости.
- •Расстояние от точки до прямой в пространстве – теория, примеры, решения.
- •Первый способ нахождения расстояния от точки до прямойaв пространстве.
- •Второй способ, позволяющий находить расстояние от точки до прямойaв пространстве.
- •33. Условия параллельности и перпендикулярности прямых в пространстве.
- •34. Взаимное расположение прямых в пространстве и прямой с плоскостью.
- •35. Классическое уравнение эллипса (вывод) и его построение. Каноническое уравнение эллипса имеет вид , где– положительные действительные числа, причём.Как построить эллипс?
- •36. Классическое уравнение гиперболы (вывод) и его построение. Асимптоты.
- •37. Каноническое уравнение параболы (вывод) и построение.
- •38. Функция. Основные определения. Графики основных элементарных функций.
- •39. Числовые последовательности. Предел числовой последовательности.
- •40. Бесконечно малые и бесконечно большие величины. Теорема о связи между ними, свойства.
- •41. Теоремы о действиях над переменными величинами, имеющими конечные пределы.
- •42. Число e.
- •Содержание
- •Способы определения
- •Свойства
- •История
- •Приближения
- •43. Определение предела функции. Раскрытие неопределённостей.
- •44. Замечательные пределы, их вывод. Эквивалентные бесконечно малые величины.
- •Содержание
- •Первый замечательный предел
- •Второй замечательный предел
- •45. Односторонние пределы. Непрерывность и разрывы функции. Односторонние пределы
- •Левый и правый пределы функции
- •Точка разрыва первого рода
- •Точка разрыва второго рода
- •Точка устранимого разрыва
- •46. Определение производной. Геометрический смысл, механический смысл производной. Уравнения касательной и нормали к кривой и точке.
- •47. Теоремы о производной обратной, сложной функций.
- •48. Производные простейших элементарных функций.
- •49. Дифференцирование параметрических, неявных и степенно-показательных функций.
- •21. Дифференцирование неявных и параметрически заданных функций
- •21.1. Неявно заданная функция
- •21.2. Функция, заданная параметрически
- •50. Производные высших порядков. Формула Тейлора.
- •51. Дифференциал. Применение дифференциала к приближенным вычислениям.
- •52. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.
- •53. Теорема о необходимом и достаточном условиях монотонности функции.
- •54. Определение максимума, минимума функции. Теоремы о необходимом и достаточном условиях существования экстремума функции.
- •Теорема (необходимое условие экстремума)
- •55. Выпуклость и вогнутость кривых. Точки перегиба. Теоремы о необходимом и достаточном условиях существования точек перегиба.
- •Доказательство
- •57. Определители n-ого порядка, их свойства.
- •58. Матрицы и действия над ними. Ранг матрицы.
- •Определение
- •Связанные определения
- •Свойства
- •Линейное преобразование и ранг матрицы
- •59. Обратная матрица. Теорема о существовании обратной матрицы.
- •60. Системы линейных уравнений. Матричное решение систем линейных уравнений. Правило Крамера. Метод Гаусса. Теорема Кронекера-Капелли.
- •Решение систем линейных алгебраических уравнений, методы решения, примеры.
- •Определения, понятия, обозначения.
- •Решение элементарных систем линейных алгебраических уравнений.
- •Решение систем линейных уравнений методом Крамера.
- •Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
- •Решение систем линейных уравнений методом Гаусса.
- •Решение систем линейных алгебраических уравнений общего вида.
- •Теорема Кронекера – Капелли.
- •Метод Гаусса для решения систем линейных алгебраических уравнений общего вида.
- •Запись общего решения однородных и неоднородных систем линейных алгебраических с помощью векторов фундаментальной системы решений.
- •Решение систем уравнений, сводящихся к слау.
- •Примеры задач, сводящихся к решению систем линейных алгебраических уравнений.
44. Замечательные пределы, их вывод. Эквивалентные бесконечно малые величины.
Как показывает
приведённый выше пример
2.36, пределы отношения бесконечно
малых можно упрощать, откидывая бесконечно
малые слагаемые большего порядка и
заменяя множители в числителе и
знаменателе на эквивалентные бесконечно
малые. Для того, чтобы этот способ
вычисления пределов (точнее, раскрытия
неопределённостей вида![]() )
можно было применять к возможно большему
числу примеров, мы должны иметь достаточно
большой запас известных пар эквивалентных
бесконечно малых величин. Для наиболее
употребительной базы
)
можно было применять к возможно большему
числу примеров, мы должны иметь достаточно
большой запас известных пар эквивалентных
бесконечно малых величин. Для наиболее
употребительной базы![]() создадим
такой запас в виде таблицы "стандартных"
эквивалентных бесконечно малых.
создадим
такой запас в виде таблицы "стандартных"
эквивалентных бесконечно малых.
Поскольку
в этой таблице мы всегда будем рассматривать
базу
![]() ,
для простоты записи обозначение этой
базы будем пропускать и писать знак
,
для простоты записи обозначение этой
базы будем пропускать и писать знак![]() вместо
вместо![]() .
.
1)
![]() .
Эту формулу мы уже доказали и использовали
в примерах. Эквивалентность
.
Эту формулу мы уже доказали и использовали
в примерах. Эквивалентность![]() и
и![]() при
при![]() означает
в точности, что первый замечательный
предел равен 1.
означает
в точности, что первый замечательный
предел равен 1.
2)
![]() .
Эта эквивалентность тоже была доказана
выше в одном из примеров.
.
Эта эквивалентность тоже была доказана
выше в одном из примеров.
3)
![]() .
Докажем эту эквивалентность:
.
Докажем эту эквивалентность:
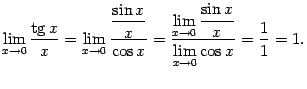
4)
![]() .
Докажите это в качестве упражнения,
сделав замену
.
Докажите это в качестве упражнения,
сделав замену![]() и
применив предыдущую табличную формулу.
и
применив предыдущую табличную формулу.
5)
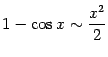 .
Для доказательства воспользуемся
формулой
.
Для доказательства воспользуемся
формулой![]() .
Далее, имеем:
.
Далее, имеем:

Это означает, что доказываемая эквивалентность имеет место.
6)
![]() (
(![]() ).
Для доказательства этой эквивалентности
сделаем такое преобразование:
).
Для доказательства этой эквивалентности
сделаем такое преобразование:
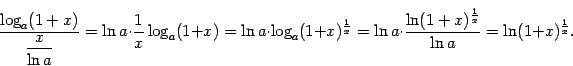
Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:
![]()
и мы доказали формулу 6.
В
частном случае, при
![]() ,
получаем эквивалентность
,
получаем эквивалентность
![]() )
)
![]() .
.
7)
![]() (
(![]() ).
Для доказательства сделаем замену
).
Для доказательства сделаем замену![]() и
выразим
и
выразим![]() через
через![]() :
:![]() .
Согласно формуле 6,
.
Согласно формуле 6,![]() при
при![]() ,
откуда
,
откуда![]() .
Из непрерывности логарифма следует,
что
.
Из непрерывности логарифма следует,
что![]() и,
значит,
и,
значит,![]() при
при![]() .
В этой формуле осталось лишь сменить
обозначение переменного
.
В этой формуле осталось лишь сменить
обозначение переменного![]() на
на![]() ,
чтобы получить формулу 7.
,
чтобы получить формулу 7.
В
частном случае, при
![]() ,
получаем эквивалентность
,
получаем эквивалентность
![]() )
)
![]() .
.
Сведём
теперь полученные формулы в итоговую
таблицу. Всюду в ней
![]() .
.
|
1) |
|
|
2) |
|
|
3) |
|
|
4) |
|
|
5) |
|
|
6) |
|
|
|
|
|
7) |
|
|
|
|
Приведём
примеры применения табличных формул
для раскрытия неопределённостей вида
![]() .
.
Замеча́тельные преде́лы— термин, использующийся в советских и российских учебниках поматематическому анализудля обозначения некоторых широко известныхматематических тождествсо взятиемпредела. Особенно известны:
Первый замечательный предел:
![]()
Второй замечательный предел:
![]()
Содержание
1Первый замечательный предел
2Второй замечательный предел
3Литература
4См. также
Первый замечательный предел
![]()
Доказательство
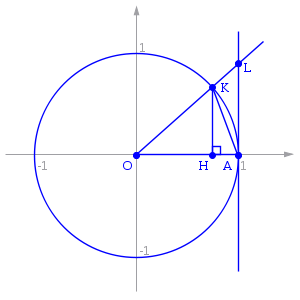
Рассмотрим
односторонние
пределы![]() и
и![]() и
докажем, что они равны 1.
и
докажем, что они равны 1.
Пусть
![]() .
Отложим этот угол на единичной окружности
(
.
Отложим этот угол на единичной окружности
(![]() ).
).
Точка
K— точка пересечения луча с
окружностью, а точкаL— с
касательной к единичной окружности в
точке![]() .
ТочкаH— проекция точкиKна
осьOX.
.
ТочкаH— проекция точкиKна
осьOX.
Очевидно, что:
![]() (1)
(1)
(где
![]() —
площадь сектора
—
площадь сектора![]() )
)
![]()
![]()
![]()
(из
![]() :
:![]() )
)
Подставляя в (1), получим:
![]()
Так
как при
![]() :
:
![]()
Умножаем
на
![]() :
:
![]()
Перейдём к пределу:
![]()
![]()
![]()
Найдём левый односторонний предел:
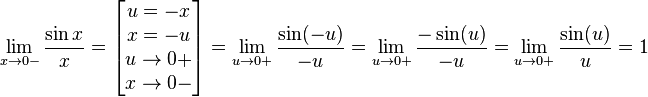
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
Доказательство следствий [показать]
Второй замечательный предел
![]() или
или
![]()
Доказательство второго замечательного предела:
Доказательство для натуральных значений x [показать]
![]() Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что
Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что
![]() .
Рассмотрим два случая:
.
Рассмотрим два случая:
1.
Пусть
![]() .
Каждое значение x заключено между двумя
положительными целыми числами:
.
Каждое значение x заключено между двумя
положительными целыми числами:![]() ,
где
,
где![]() —
это целая часть x.
—
это целая часть x.
Отсюда следует:
![]() ,
поэтому
,
поэтому
![]() .
.
Если
![]() ,
то
,
то![]() .
Поэтому, согласно пределу
.
Поэтому, согласно пределу![]() ,
имеем:
,
имеем:

![]() .
.
По признаку (о пределе промежуточной
функции) существования пределов
![]() .
.
2.
Пусть
![]() .
Сделаем подстановку
.
Сделаем подстановку![]() ,
тогда
,
тогда
![]()
![]() .
.
Из
двух этих случаев вытекает, что
![]() для
вещественного x.
для
вещественного x.![]()
Следствия


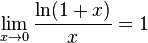

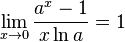 для
для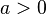 ,
,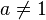
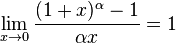

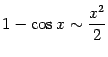 .
.