Второй способ, позволяющий найти расстояние от заданной точки до заданной прямой на плоскости.

Следующая теорема отвечает на вопрос: «Как найти расстояние от заданной точки до заданной прямой на плоскости»?

Теорема.

В прямоугольной системе координат Oxyна плоскости расстояние от точкидо прямойa, заданной нормальным уравнением прямой вида, равно модулю значения выражения, находящегося в левой части нормального уравнения прямой, вычисленного при, то есть,.

Доказательство.

Так как прямой aв прямоугольной системе координатOxyна плоскости соответствует нормальное уравнение прямой, то-нормальный вектор прямойaединичной длины, а расстояние от начала координат до прямойaравноpединиц. Изобразим эти данные на чертеже, а также добавим точку,радиус-вектор точкиМ₁-, построим искомое расстояние от точкиМ₁до прямойa-, покажем проекцииМ₂иH₂точекМ₁иH₁соответственно на прямую, проходящую через точкуOи имеющую направляющий вектор, обозначимчисловую проекцию векторана направление векторакак.

В зависимости от расположения точки М₁относительно прямойaвозможны следующие варианты.

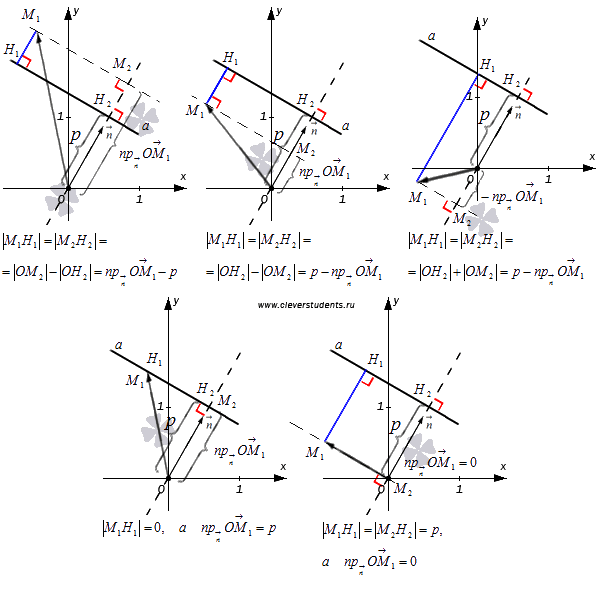
Все полученные результаты можно описать одной формулой: . Осталось привести полученное равенство к виду, то есть показать, что.

Определение скалярного произведения векторовдает нам равенство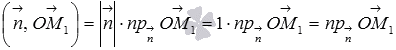, а это же самое скалярное произведение в координатной форме имеет вид, следовательно,. Тогда, что и требовалось доказать.

Таким образом, чтобы найти расстояние от точки до прямойa на плоскости нужно:

• получить нормальное уравнение прямой aв виде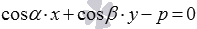(если оно сразу не дано);

• вычислить значение выражения 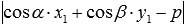- полученное значение является искомым расстоянием.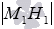

Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости.

Рассмотрим применение разобранных методов для нахождения расстояния от заданной точки до заданной прямой на плоскости при решении примера.

Пример.

Найдите расстояние от точки до прямой.

Решение.

Сначала решим задачу первым способом.

В условии задачи нам дано общее уравнение прямой aвида. Найдем общее уравнение прямойb, которая проходит через заданную точкуперпендикулярно прямой.

Так как прямая bперпендикулярна прямойa, тонаправляющий вектор прямойbесть нормальный вектор заданной прямой, то есть, направляющий вектор прямойbимеет координаты. Теперь мы можем записатьканоническое уравнение прямой bна плоскости, так как знаем координаты точкиМ₁, через которую проходит прямаяb, и координаты направляющего вектора прямойb: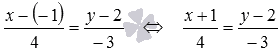. От полученного канонического уравнения прямойbперейдем к общему уравнению прямой:.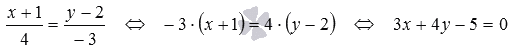

Теперь найдем координаты точки пересечения прямых aиb(обозначим ееH₁), решив систему уравнений, составленную из общих уравнений прямыхaиb(при необходимости обращайтесь к статьерешение систем линейных уравнений):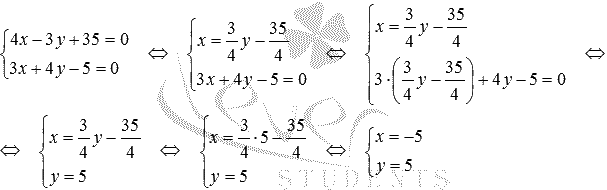

Таким образом, точка H₁имеет координаты.

Осталось вычислить искомое расстояние от точки М₁до прямойaкак расстояние между точкамии:.

Второй способ решения задачи.

Получим нормальное уравнение заданной прямой. Для этого вычислим значение нормирующего множителя и умножим на него обе части исходного общего уравнения прямой (об этом мы говорили в разделеприведение общего уравнения прямой к нормальному виду).

Нормирующий множитель равен 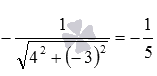, тогда нормальное уравнение прямой имеет вид. Теперь берем выражение, стоящее в левой части полученного нормального уравнения прямой, и вычисляем его значение при:.

Искомое расстояние от заданной точки до заданной прямойравно абсолютной величине полученного значения, то есть, пяти ().

Ответ:

расстояние от точки до прямойравно5.

Очевидно, достоинством метода нахождения расстояния от точки до прямой на плоскости, основанного на использовании нормального уравнения прямой, является сравнительно меньший объем вычислительной работы. В свою очередь первый способ нахождения расстояния от точки до прямой интуитивно понятен и отличается последовательностью и логичностью.

Пример.

На плоскости зафиксирована прямоугольная система координат Oxy, задана точкаи прямая. Найдите расстояние от заданной точки до заданной прямой.

Решение.

Первый способ.

Можно от заданного уравнения прямой с угловым коэффициентом перейти к общему уравнению этой прямой и действовать так же, как в разобранном выше примере.

Но можно поступить и иначе.

Мы знаем, что произведение угловых коэффициентов перпендикулярных прямых равно -1(смотрите статьюперпендикулярные прямые, перпендикулярность прямых). Поэтому угловой коэффициент прямой, которая перпендикулярна заданной прямой, равен-2. Тогда уравнение прямой, перпендикулярной заданной прямой и проходящей через точку, имеет вид.

Теперь найдем координаты точки H₁- точки пересечения прямыхи:

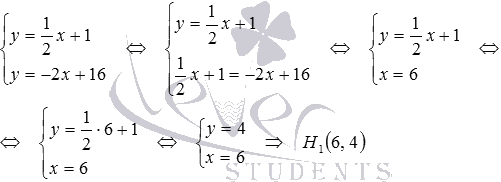
Таким образом, искомое расстояние от точки до прямойравно расстоянию между точкамии:

Второй способ.

Перейдем от заданного уравнения прямой с угловым коэффициентом к нормальному уравнению этой прямой: , нормирующий множитель равен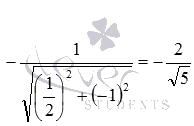, следовательно, нормальное уравнение заданной прямой имеет вид. Теперь вычисляем требуемое расстояния от точкидо прямой: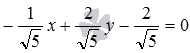

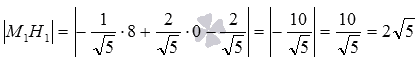
Ответ:

.

Пример.

Вычислите расстояние от точки до прямойи до прямой.

Решение.

Получим нормальное уравнение прямой :.

Теперь вычислим расстояние от точки до прямой:.

Нормирующий множитель для уравнения прямой вида равен-1. Тогда нормальное уравнение этой прямой имеет вид.

Теперь мы можем вычислить расстояние от точки до прямой- оно равно.

Ответ:

и 5.

В заключении отдельно рассмотрим, как находится расстояние от заданной точки плоскости до координатных прямых OxиOy.

В прямоугольной системе координат Oxyкоординатную прямуюOyзадаетнеполное общее уравнение прямойx=0, а координатную прямуюOx– уравнениеy=0. Эти уравнения являются нормальными уравнениями прямыхOyиOx, следовательно, расстояние от точкидо этих прямых вычисляются по формуламисоответственно.

Пример.

На плоскости введена прямоугольная система координат Oxy. Найдите расстояния от точкидо координатных прямых.

Решение.

Расстояние от заданной точки М₁до координатной прямойOx(она задается уравнениемy=0) равно модулю ординаты точкиМ₁, то есть,.

Расстояние от заданной точки М₁до координатной прямойOy(ей соответствует уравнениеx=0) равно абсолютной величине абсциссы точкиМ₁:.

Ответ:

расстояние от точки М₁до прямойOxравно6, а расстояние от заданной точки до координатной прямойOyравно.

К началу страницы