32. Расстояние от точки до прямой на плоскости (вывод).

Расстояние от точки до прямой определяется через расстояние от точки до точки. Покажем как это делается.

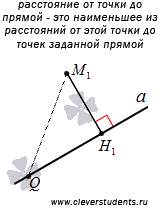
Пусть на плоскости или в трехмерном пространстве задана прямая aи точкаM₁, не лежащая на прямойa. Проведем через точкуM₁прямуюb, перпендикулярную прямойa. Обозначим точку пересечения прямыхaиbкакH₁. ОтрезокM₁H₁называетсяперпендикуляром, проведенным из точкиM₁к прямойa.

Определение.

Расстоянием от точки M₁ до прямой aназывают расстояние между точкамиM₁иH₁.

Однако чаще встречается определение расстояния от точки до прямой, в котором фигурирует длина перпендикуляра.

Определение.

Расстояние от точки до прямой– это длина перпендикуляра, проведенного из данной точки к данной прямой.

Это определение эквивалентно первому определению расстояния от точки до прямой.

Обратите внимание на то, что расстояние от точки до прямой – это наименьшее из расстояний от этой точки до точек заданной прямой. Покажем это.

Возьмем на прямой aточкуQ, не совпадающую с точкойM₁. ОтрезокM₁Qназываютнаклонной, проведенной из точкиM₁к прямойa. Нам нужно показать, что перпендикуляр, проведенный из точкиM₁к прямойa, меньше любой наклонной, проведенной из точкиM₁к прямойa. Это действительно так: треугольникM₁QH₁прямоугольный с гипотенузойM₁Q, а длина гипотенузы всегда больше длины любого из катетов, следовательно,.

К началу страницы

Расстояние от точки до прямой на плоскости – теория, примеры, решения.

В зависимости от исходных данных для нахождения расстояния от точки до прямой можно использовать различные методы геометрии: теорему Пифагора, определения синуса, косинуса, тангенса угла, признаки равенства и подобия треугольников и т.п. Множество подобных задач решается на уроках геометрии в средней школе.

Если же при нахождении расстояния от точки до прямой есть возможность ввести прямоугольную систему координат, то можно воспользоваться методом координат. В этом пункте статьи мы подробно остановимся на двух способах нахождения расстояния от точкиM₁до прямойa, которые заданы в прямоугольной декартовой системе координатOxyна плоскости. В первом случае расстояние от точкиM₁до прямойaмы будем искать как расстояние от точкиM₁до точкиH₁, гдеH₁– основание перпендикуляра, опущенного из точкиM₁на прямуюa. Во втором способе нахождения расстояния от точкиM₁до прямойaбудем использоватьнормальное уравнение прямойa.

Итак, поставим перед собой следующую задачу: пусть на плоскости зафиксирована прямоугольная система координат Oxy, задана точка, прямаяaи требуется найти расстояниеот точкиM₁до прямойa. Разберем по-очереди два способа ее решения.

Первый способ нахождения расстояния от заданной точки до заданной прямой на плоскости.

Если мы определим координаты точкиH₁, то искомое расстояниемы сможем вычислить, используя формулу для нахождения расстояния от точкиM₁до точкиH₁по их координатам:.

Осталось разобраться с нахождением координат точки H₁.

Мы знаем, что прямой линии в прямоугольной системе координат Oxyсоответствует некотороеуравнение прямой на плоскости. Будем считать, что способ задания прямойaв условии задачи позволяет написатьобщее уравнение прямойaилиуравнение прямой с угловым коэффициентом. После этого мы можем составитьуравнение прямой, проходящей через заданную точку M₁перпендикулярно заданной прямойa. Обозначим эту прямую буквойb. Тогда точкаH₁– это точка пересечения прямыхaиb, следовательно, координаты точкиH₁можно определить, обратившись к материалу статьикоординаты точки пересечения двух прямых.

Итак, мы получили алгоритм для нахождения расстояния от заданной точки до заданной прямойa:

• находим общее уравнение прямой aвида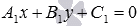или уравнение прямойaс угловым коэффициентом;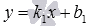

• получаем общее уравнение прямой bвида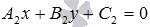или уравнение прямойbс угловым коэффициентом вида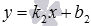, учитывая, что прямаяbпроходит через заданную точкуM₁и перпендикулярна заданной прямойa;

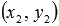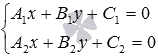• определяем координаты точкиH₁- точки пересечения прямыхaиb, решая систему линейных уравненийили;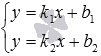

• вычисляем требуемое расстояние от точки M₁до прямойaпо формуле.