
- •1. Определение вектора. Длина вектора. Коллинеарность, компланарность векторов.
- •2. Умножение вектора на число. Свойства операции.
- •3. Сложение векторов, вычитание векторов.
- •4. Базис на плоскости. Теорема о разложении любого вектора по трём базисным векторам.
- •5. Базис в пространстве. Теорема о разложении любого вектора по трем базисным векторам.
- •6. Линейная зависимость векторов.
- •7. Декартова система координат на плоскости и в пространстве, координаты вектора.
- •8. Геометрический смысл координат вектора. Проекция вектора на координатные оси. Направляющие косинусы вектора
- •9. Деление отрезка в данном отношении.
- •6.4. Некоторые приложения скалярного произведения
- •11. Выражение скалярного произведения вектора через координаты сомножителей. Теорема.
- •12. Длина вектора, длина отрезка, угол между векторами, условие перпендикулярности векторов.
- •13. Векторное произведение векторов, его свойства. Площадь параллелограмма.
- •14. Смешанное произведение векторов, его свойства. Условие компланарности вектора. Объем параллелепипеда. Объём пирамиды.
- •15. Способы задания прямой на плоскости.
- •16. Нормальное уравнение прямой на плоскости (вывод). Геометрический смысл коэффициентов.
- •17. Уравнение прямой на плоскости в отрезках (вывод).
- •Приведение общего уравнения плоскости к уравнению плоскости в отрезках.
- •18. Уравнение прямой на плоскости с угловым коэффициентом (вывод).
- •19. Уравнение прямой на плоскости, проходящей через две точки (вывод).
- •20. Угол между прямыми на плоскости (вывод).
- •21. Расстояние от точки до прямой на плоскости (вывод).
- •22. Условия параллельности и перпендикулярности прямых на плоскости (вывод).
- •23. Уравнение плоскости. Нормальное уравнение плоскости (вывод). Геометрический смысл коэффициентов.
- •24. Уравнение плоскости в отрезках (вывод).
- •25. Уравнение плоскости, проходящей через три точки (вывод).
- •26. Угол между плоскостями (вывод).
- •27. Расстояние от точки до плоскости (вывод).
- •28. Условия параллельности и перпендикулярности плоскостей (вывод).
- •29. Уравнения прямой в r3. Уравнения прямой, проходящей через две фиксированные точки (вывод).
- •30. Канонические уравнения прямой в пространстве (вывод).
- •Составление канонических уравнений прямой в пространстве.
- •Частные случаи канонических уравнений прямой в пространстве.
- •Канонические уравнения прямой проходящей через две заданные точки пространства.
- •Переход от канонических уравнений прямой в пространстве к другим видам уравнений прямой.
- •31. Угол между прямыми (вывод).
- •32. Расстояние от точки до прямой на плоскости (вывод).
- •Расстояние от точки до прямой на плоскости – теория, примеры, решения.
- •Первый способ нахождения расстояния от заданной точки до заданной прямой на плоскости.
- •Второй способ, позволяющий найти расстояние от заданной точки до заданной прямой на плоскости.
- •Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости.
- •Расстояние от точки до прямой в пространстве – теория, примеры, решения.
- •Первый способ нахождения расстояния от точки до прямойaв пространстве.
- •Второй способ, позволяющий находить расстояние от точки до прямойaв пространстве.
- •33. Условия параллельности и перпендикулярности прямых в пространстве.
- •34. Взаимное расположение прямых в пространстве и прямой с плоскостью.
- •35. Классическое уравнение эллипса (вывод) и его построение. Каноническое уравнение эллипса имеет вид , где– положительные действительные числа, причём.Как построить эллипс?
- •36. Классическое уравнение гиперболы (вывод) и его построение. Асимптоты.
- •37. Каноническое уравнение параболы (вывод) и построение.
- •38. Функция. Основные определения. Графики основных элементарных функций.
- •39. Числовые последовательности. Предел числовой последовательности.
- •40. Бесконечно малые и бесконечно большие величины. Теорема о связи между ними, свойства.
- •41. Теоремы о действиях над переменными величинами, имеющими конечные пределы.
- •42. Число e.
- •Содержание
- •Способы определения
- •Свойства
- •История
- •Приближения
- •43. Определение предела функции. Раскрытие неопределённостей.
- •44. Замечательные пределы, их вывод. Эквивалентные бесконечно малые величины.
- •Содержание
- •Первый замечательный предел
- •Второй замечательный предел
- •45. Односторонние пределы. Непрерывность и разрывы функции. Односторонние пределы
- •Левый и правый пределы функции
- •Точка разрыва первого рода
- •Точка разрыва второго рода
- •Точка устранимого разрыва
- •46. Определение производной. Геометрический смысл, механический смысл производной. Уравнения касательной и нормали к кривой и точке.
- •47. Теоремы о производной обратной, сложной функций.
- •48. Производные простейших элементарных функций.
- •49. Дифференцирование параметрических, неявных и степенно-показательных функций.
- •21. Дифференцирование неявных и параметрически заданных функций
- •21.1. Неявно заданная функция
- •21.2. Функция, заданная параметрически
- •50. Производные высших порядков. Формула Тейлора.
- •51. Дифференциал. Применение дифференциала к приближенным вычислениям.
- •52. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.
- •53. Теорема о необходимом и достаточном условиях монотонности функции.
- •54. Определение максимума, минимума функции. Теоремы о необходимом и достаточном условиях существования экстремума функции.
- •Теорема (необходимое условие экстремума)
- •55. Выпуклость и вогнутость кривых. Точки перегиба. Теоремы о необходимом и достаточном условиях существования точек перегиба.
- •Доказательство
- •57. Определители n-ого порядка, их свойства.
- •58. Матрицы и действия над ними. Ранг матрицы.
- •Определение
- •Связанные определения
- •Свойства
- •Линейное преобразование и ранг матрицы
- •59. Обратная матрица. Теорема о существовании обратной матрицы.
- •60. Системы линейных уравнений. Матричное решение систем линейных уравнений. Правило Крамера. Метод Гаусса. Теорема Кронекера-Капелли.
- •Решение систем линейных алгебраических уравнений, методы решения, примеры.
- •Определения, понятия, обозначения.
- •Решение элементарных систем линейных алгебраических уравнений.
- •Решение систем линейных уравнений методом Крамера.
- •Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
- •Решение систем линейных уравнений методом Гаусса.
- •Решение систем линейных алгебраических уравнений общего вида.
- •Теорема Кронекера – Капелли.
- •Метод Гаусса для решения систем линейных алгебраических уравнений общего вида.
- •Запись общего решения однородных и неоднородных систем линейных алгебраических с помощью векторов фундаментальной системы решений.
- •Решение систем уравнений, сводящихся к слау.
- •Примеры задач, сводящихся к решению систем линейных алгебраических уравнений.
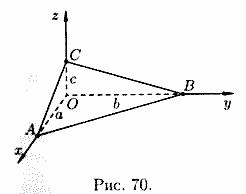
24. Уравнение плоскости в отрезках (вывод).
Уравнение плоскости в отрезках
Пусть плоскость отсекает на осях Ох, Оу и Оz соответственно отрезки a, b и c, т. е. проходит через три точки A(a;0;0), B(0;b;0) и C(0;0;c) (см.рис. 70). Подставляя координаты этих точек в уравнение (12.6), получаем
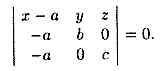
Раскрыв
определитель, имеем
![]() ,
т. е.
,
т. е.![]()
![]() или
или
![]() (12.7)
(12.7)
Уравнение (12.7) называется уравнением плоскости в отрезках на осях. Им удобно пользоваться при построении плоскости.
25. Уравнение плоскости, проходящей через три точки (вывод).
Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данные точки M1(x1;y1;z1), М2(x2;y2;z2) и М3(х3,y3,z3), не лежащие на одной прямой.
Возьмем
на плоскости произвольную точку M(x;y;z)
и составим векторы
![]() ,
,![]() ,
,![]() .
Эти векторы лежат на плоскости Q,
следовательно, они компланарны. Используем
условие компланарности трех векторов
(их смешанное произведение равно нулю),
получаем
.
Эти векторы лежат на плоскости Q,
следовательно, они компланарны. Используем
условие компланарности трех векторов
(их смешанное произведение равно нулю),
получаем![]() ,
т. е.
,
т. е.
 (12.6)
(12.6)
Уравнение (12.6) есть уравнение плоскости, проходящей через три данные точки.
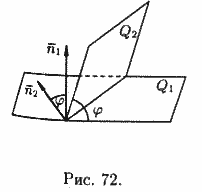
26. Угол между плоскостями (вывод).
Пусть заданы две плоскости Q1 и Q2:
![]()
Под углом между плоскостями Q1 и Q2 понимается один из двугранных углов, образованных этими плоскостями.
Угол
между нормальными векторами
![]() и
и![]() плоскостей
Q1
и Q2
равен одному из этих углов (см. рис. 72).
плоскостей
Q1
и Q2
равен одному из этих углов (см. рис. 72).
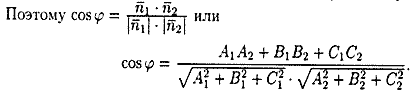
Для нахождения острого угла следует взять модуль правой части.
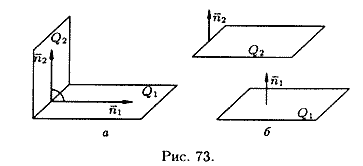
Если
плоскости Q1
и Q2
перпендикулярны (см. рис. 73,
а), то таковы же их нормали, т. е.
![]() (и
наоборот). Но тогда
(и
наоборот). Но тогда![]() ,
т. е.
,
т. е.![]() .
Полученное равенство есть условие
перпендикулярности двух плоскостей Q1
и Q2.
.
Полученное равенство есть условие
перпендикулярности двух плоскостей Q1
и Q2.
Если
плоскости Q1
и Q2
параллельны (см. рис. 73, б), то будут
параллельны и их нормали
![]() и
и![]() (и
наоборот). Но тогда, как известно
координаты векторов пропорциональны:
(и
наоборот). Но тогда, как известно
координаты векторов пропорциональны:![]() .
Это и есть уcловиє параллельности двух
плоскостей Q1
и Q2.
.
Это и есть уcловиє параллельности двух
плоскостей Q1
и Q2.
27. Расстояние от точки до плоскости (вывод).
Пусть
задана точка
![]() и
плоскость Q своим уравнением
и
плоскость Q своим уравнением![]() .
Расстояние d от точки
.
Расстояние d от точки![]() до
плоскости Q находится по формуле
до
плоскости Q находится по формуле
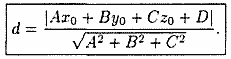
Вывод
этой формулы такой же, как вывод формулы
расстояния от точки
![]() до
прямой
до
прямой![]() .
.
Расстояние
d от точки M0
до плоскости Q равно модулю проекции
вектора
![]() ,
где
,
где![]() —
произвольная точка плоскости Q, на
направление нормального вектора
—
произвольная точка плоскости Q, на
направление нормального вектора![]() (см.
рис. 74). Следовательно,
(см.
рис. 74). Следовательно,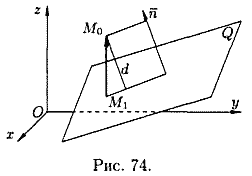
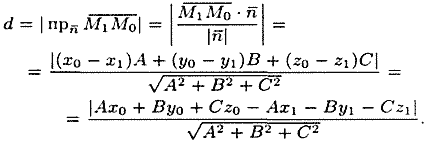
А
так как точка
![]() принадлежит
плоскости Q, то
принадлежит
плоскости Q, то
![]()
Поэтому
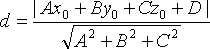 .
Отметим, что если плоскость Q задана
уравнением
.
Отметим, что если плоскость Q задана
уравнением![]() ,
то расстояние от точки
,
то расстояние от точки![]() до
плоскости Q может быть найдено по формуле
до
плоскости Q может быть найдено по формуле
![]()
28. Условия параллельности и перпендикулярности плоскостей (вывод).
Если
плоскости Q1
и Q2
перпендикулярны (см. рис. 73,
а), то таковы же их нормали, т. е.
![]() (и
наоборот). Но тогда
(и
наоборот). Но тогда![]() ,
т. е.
,
т. е.![]() .
Полученное равенство есть условие
перпендикулярности двух плоскостей Q1
и Q2.
.
Полученное равенство есть условие
перпендикулярности двух плоскостей Q1
и Q2.
Если
плоскости Q1
и Q2
параллельны (см. рис. 73, б), то будут
параллельны и их нормали
![]() и
и![]() (и
наоборот). Но тогда, как известно
координаты векторов пропорциональны:
(и
наоборот). Но тогда, как известно
координаты векторов пропорциональны:![]() .
Это и есть условие параллельности двух
плоскостей Q1
и Q2.
.
Это и есть условие параллельности двух
плоскостей Q1
и Q2.
29. Уравнения прямой в r3. Уравнения прямой, проходящей через две фиксированные точки (вывод).
Прежде чем получить уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат на плоскости, вспомним некоторые факты.
Одна из аксиом геометрии гласит, что через две несовпадающие точки на плоскости можно провести единственную прямую. Другими словами, задав две точки на плоскости, мы однозначно определяем прямую линию, которая через эти две точки проходит (при необходимости обращайтесь к разделу способы задания прямой на плоскости).
Пусть на плоскости зафиксирована прямоугольная декартова система координатOxy. В этой системе координат любой прямой линии соответствует некотороеуравнение прямой на плоскости. С этой же прямой неразрывно связаннаправляющий вектор прямой. Этих знаний вполне достаточно, чтобы составить уравнение прямой, проходящей через две заданные точки.
Сформулируем
условие задачи: составить уравнение
прямой a, которая в прямоугольной
декартовой системе координатOxyпроходит через две несовпадающие точки![]() и
и![]() .
.
Покажем самое простое и универсальное решение этой задачи.
Нам
известно, что каноническое
уравнение прямой на плоскостивида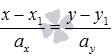 задает
в прямоугольной системе координатOxyпрямую линию, проходящую через точку
задает
в прямоугольной системе координатOxyпрямую линию, проходящую через точку![]() и
имеющую направляющий вектор
и
имеющую направляющий вектор![]() .
.
Напишем
каноническое уравнение прямой a,
проходящей через две заданные точки![]() и
и![]() .
.
Очевидно,
направляющим вектором прямой a,
которая проходит через точкиМ1иМ2, является вектор![]() ,
он имеет координаты
,
он имеет координаты![]() (при
необходимости смотрите статьювычисление
координат вектора по координатам точек
его конца и начала). Таким образом, мы
имеем все необходимые данные, чтобы
написать каноническое уравнение прямойa– координаты ее направляющего
вектора
(при
необходимости смотрите статьювычисление
координат вектора по координатам точек
его конца и начала). Таким образом, мы
имеем все необходимые данные, чтобы
написать каноническое уравнение прямойa– координаты ее направляющего
вектора![]() и
координаты лежащей на ней точки
и
координаты лежащей на ней точки![]() (и
(и![]() ).
Оно имеет вид
).
Оно имеет вид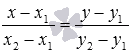 (или
(или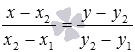 ).
).
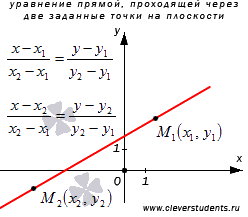
Также
мы можем записать параметрические
уравнения прямой на плоскости,
проходящей через две точки![]() и
и![]() .
Они имеют вид
.
Они имеют вид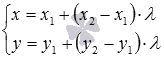 или
или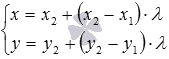 .
.
Разберем решение примера.
Пример.
Напишите
уравнение прямой, которая проходит
через две заданные точки
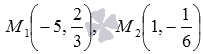 .
.
Решение.
Мы
выяснили, что каноническое уравнение
прямой, проходящей через две точки с
координатами
![]() и
и![]() ,
имеет вид
,
имеет вид .
.
Из
условия задачи имеем
![]() .
Подставим эти данные в уравнение
.
Подставим эти данные в уравнение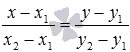 .
Получаем
.
Получаем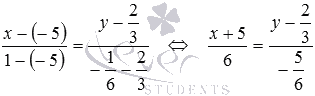 .
.
Ответ:
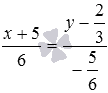 .
.
Если нам потребуется не каноническое уравнение прямой и не параметрические уравнения прямой, проходящей через две заданные точки, а уравнение прямой другого вида, то от канонического уравнения прямой всегда можно к нему прийти.
Пример.
Составьте
общее
уравнение прямой, которая в прямоугольной
системе координатOxyна плоскости
проходит через две точки![]() и
и![]() .
.
Решение.
Сначала
напишем каноническое уравнение прямой,
проходящей через две заданные точки.
Оно имеет вид
![]() .
Теперь приведем полученное уравнение
к требуемому виду:
.
Теперь приведем полученное уравнение
к требуемому виду:![]() .
.
Ответ:
![]() .
.
На этом можно и закончить с уравнением прямой, проходящей через две заданные точки в прямоугольной системе координат на плоскости. Но хочется напомнить, как мы решали такую задачу в средней школе на уроках алгебры.
В
школе нам было известно лишь уравнение
прямой с угловым коэффициентомвида![]() .
Найдем значение углового коэффициентаkи числаb, при которых уравнение
.
Найдем значение углового коэффициентаkи числаb, при которых уравнение![]() определяет
в прямоугольной системе координатOxyна плоскости прямую линию, проходящую
через точки
определяет
в прямоугольной системе координатOxyна плоскости прямую линию, проходящую
через точки![]() и
и![]() при
при![]() .
(Если жеx1=x2,
то угловой коэффициент прямой бесконечен,
а прямуюМ1М2определяетобщее
неполное уравнение прямойвидаx-x1=0).
.
(Если жеx1=x2,
то угловой коэффициент прямой бесконечен,
а прямуюМ1М2определяетобщее
неполное уравнение прямойвидаx-x1=0).
Так
как точки М1иМ2лежат на прямой, то координаты этих
точек удовлетворяют уравнению прямой![]() ,
то есть, справедливы равенства
,
то есть, справедливы равенства![]() и
и![]() .
Решая систему уравнений вида
.
Решая систему уравнений вида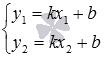 относительно
неизвестных переменныхkиb,
находим
относительно
неизвестных переменныхkиb,
находим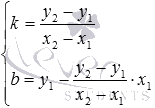 или
или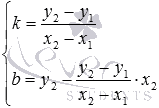 .
При этих значенияхkиbуравнение
прямой, проходящей через две точки
.
При этих значенияхkиbуравнение
прямой, проходящей через две точки![]() и
и![]() ,
принимает вид
,
принимает вид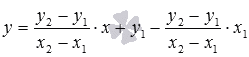 или
или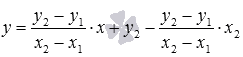 .
.
Запоминать эти формулы не имеет смысла, при решении примеров проще повторять указанные действия.
Пример.
Напишите
уравнение прямой с угловым коэффициентом,
если эта прямая проходит через точки
![]() и
и![]() .
.
Решение.
В
общем случае уравнение прямой с угловым
коэффициентом имеет вид
![]() .
Найдемkиb, при которых уравнение
.
Найдемkиb, при которых уравнение![]() соответствует
прямой, проходящей через две точки
соответствует
прямой, проходящей через две точки![]() и
и![]() .
.
Так
как точки М1иМ2лежат на прямой, то их координаты
удовлетворяют уравнению прямой![]() ,
то есть, верны равенства
,
то есть, верны равенства![]() и
и![]() .
Значенияkиbнаходим как решение
системы уравнений
.
Значенияkиbнаходим как решение
системы уравнений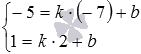 (при
необходимости обращайтесь к статьерешение
систем линейных уравнений):
(при
необходимости обращайтесь к статьерешение
систем линейных уравнений):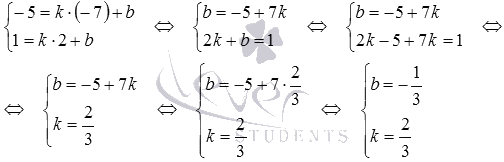
Осталось
подставить найденные значения
![]() и
и![]() в
уравнение
в
уравнение![]() .
Таким образом, искомое уравнение прямой,
проходящей через две точки
.
Таким образом, искомое уравнение прямой,
проходящей через две точки![]() и
и![]() ,
имеет вид
,
имеет вид![]() .
.
Колоссальный труд, не так ли?
Намного
проще записать каноническое уравнение
прямой, проходящей через две точки
![]() и
и![]() ,
оно имеет вид
,
оно имеет вид ,
и от него перейти к уравнению прямой с
угловым коэффициентом:
,
и от него перейти к уравнению прямой с
угловым коэффициентом:![]() .
.
Ответ:
![]() .
.
К началу страницы
Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве.
Пусть
в трехмерном пространстве зафиксирована
прямоугольная система координат Oxyz,
и заданы две несовпадающие точки![]() и
и![]() ,
через которые проходит прямаяM1M2.
Получим уравнения этой прямой.
,
через которые проходит прямаяM1M2.
Получим уравнения этой прямой.
Нам
известно, что канонические
уравнения прямой в пространствевида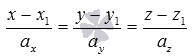 ипараметрические
уравнения прямой в пространствевида
ипараметрические
уравнения прямой в пространствевида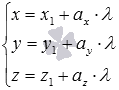 задают
в прямоугольной системе координатOxyzпрямую линию, которая проходит через
точку с координатами
задают
в прямоугольной системе координатOxyzпрямую линию, которая проходит через
точку с координатами![]() и
имеет направляющий вектор
и
имеет направляющий вектор![]() .
.
Направляющим
вектором прямой M1M2является вектор![]() ,
и эта прямая проходит через точку
,
и эта прямая проходит через точку![]() (и
(и![]() ),
тогда канонические уравнения этой
прямой имеют вид
),
тогда канонические уравнения этой
прямой имеют вид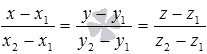 (или
(или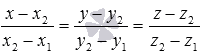 ),
а параметрические уравнения -
),
а параметрические уравнения -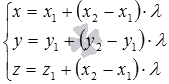 (или
(или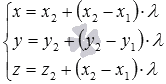 ).
).

Пример.
Напишите
уравнение прямой, которая в прямоугольной
системе координат Oxyzв трехмерном
пространстве проходит через две точки![]() и
и![]() .
.
Решение.
Мы
выяснили, что в прямоугольной системе
координат Oxyzв трехмерном пространстве
канонические уравнения прямой, которая
проходит через две точки![]() и
и![]() ,
имеют вид
,
имеют вид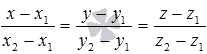 .
.
Из
условия имеем
![]() ,
тогда искомые уравнения прямой запишутся
как
,
тогда искомые уравнения прямой запишутся
как .
.
Ответ:
![]() .
.
Если
потребуется задать прямую М1М2с помощьюуравнений
двух пересекающихся плоскостей, то
сначала следует составить канонические
уравнения прямой, проходящей через две
точки![]() и
и![]() ,
и из этих уравнений получить нужные
уравнения плоскостей.
,
и из этих уравнений получить нужные
уравнения плоскостей.
