21. Расстояние от точки до прямой на плоскости (вывод).

Вывод формулы расстояния от точки до прямой

Вариант 1 

Пусть на плоскости дана прямая l : ax + by + c = 0 и точка M₁(x₁;y₁), не принадлежащая этой прямой. Найдем расстояние от точки до прямой. Под расстоянием ρ от точки M₁ до прямой l понимают длину отрезка M₀ M₁⏊l.

Для определения расстояния удобно использовать единичный вектор, коллинеарный нормальному вектору прямой.

 Пояснение: поскольку точка M₀ лежит в на прямой l, то ее координаты должны удовлетворять уравнению данной прямой, т.е. ax₀ + by₀ + c = 0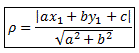Вариант 2

Если задана точка М(х₀, у₀), то расстояние до прямой Ах + Ву + С =0 определяется как .

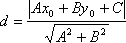  Доказательство. Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁:  (1) Координаты x₁ и у₁ могут быть найдены как решение системы уравнений: 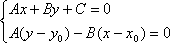Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М₀ перпендикулярно заданной прямой.  Если преобразовать первое уравнение системы к виду: A(x – x₀) + B(y – y₀) + Ax₀ + By₀ + C = 0, то, решая, получим: 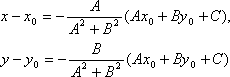Подставляя эти выражения в уравнение (1), находим: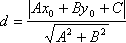. Теорема доказана.

22. Условия параллельности и перпендикулярности прямых на плоскости (вывод).

1) Если прямые R₁ и R₂ параллельны, то φ = 0. Тогда tg φ = 0 и из формулы (7) имеем k₂ - k₁ = 0 или k₂ = k₁. Таким образом, условием параллельности двух прямых на плоскости является равенство их угловых коэффициентов.

 

2) Если прямые R₁ и R₂ перпендикулярны, то φ = . Так как φ = φ₂ – φ₁ , то

φ₂ = + φ₁ и tg φ₂ = tg(+ φ₁) = ctg φ₁ = - , т.е.

 

k₂ = - . (8)

Таким образом, условие перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку.

23. Уравнение плоскости. Нормальное уравнение плоскости (вывод). Геометрический смысл коэффициентов.

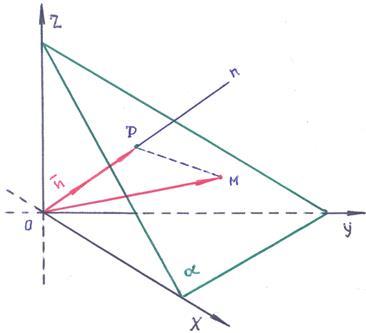
Получение уравнения плоскости в нормальном виде представляет интерес даже с формальной точки зрения: как развитие аналитических моделей геометрических фигур при переходе от двумерного пространства к 3-мерному. С другой стороны, от нормального уравнения плоскости мы ожидаем расширения наших возможностей при решении более сложных геометрических задач. Пусть точкаи. Пусть единичный векторсовпадает по направлению с вектором. Известно, что любой вектор можно представить как:, где– направляющие косинусы вектора.

Учитывая: =1, представим векторв виде:. Отметим на плоскостипроизвольную точку:==.

Используя заданные условия и принятые обозначения, запишем (используя скалярное произведение векторов и формулу для вычисления проекции вектора на направление):====×=,

откуда получаем: . (1)

Уравнение (1) называют нормальным уравнением плоскости. Если уравнение (1) рассматривать как общее уравнение плоскости, то, как легко заметить, нормальный вектор этой плоскости единичный.

Отнесёмся к выражению: формально. Учитывая способ получения нормального уравнения (1), нетрудно догадаться, что для всех точек пространства, принадлежащих плоскостивеличина=0. А что будет происходить с величиной, если выбирать произвольные точки пространства?

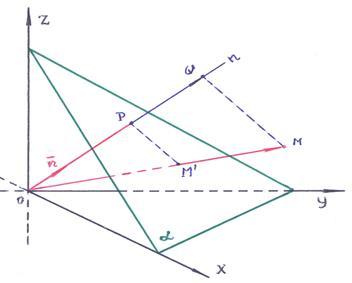
Пусть – произвольная точка пространства и– некоторая плоскость пространства. Пусть точка, причём. Пусть единичный векторсовпадает по направлению с вектороми представлен в виде:.

Найдём проекцию точки на направление: обозначим проекцию как точку. В таком случае длина отрезкаравна расстоянию точкиот начала координат. Вычислим=+. При получении нормального уравнения плоскости было показано, что=. Тогда:=,

после чего можем записать: =–==[вспомним обозначение]=.

Итак, геометрический смысл величины –отклонение произвольной точки пространства от плоскости, причём=–расстояние этой точки до этой плоскости.

Возникает вопрос: почему для нахождения расстояния потребовался модуль? Ответ легко видеть из рисунка:

а) если точки ирасполагаются по разные стороны от плоскости, то>0;

б) если точки ирасполагаются по одну сторону от плоскости, то<0.

Ещё раз отметим, что величина – это расстояние произвольной точки пространства до заданной плоскости, причёмсо знаком! Знак отражает процесс проектирования вектора на направление вектора, а именно:=. Так как векторединичный, то получаем длину отрезка:==, измеренную при помощи единичного вектора.

Если уравнение плоскости задано в общем виде: , то его можнонормировать, то есть привести к записи (1). Это делают так:

1). Умножим общее уравнение плоскости на число :. (2)

2). Пусть получили тождество: . Тогда необходимо:→;→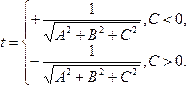(3)Замечания: 1). В результате нормализации вектор нормали плоскости преобразован в единичный вектор: =→=, причем=1.

2). Смысл правил выбора знака величины t в преобразованиях (3), будет установлен при рассмотрении задачи вычисления отклонения произвольной точки от заданной плоскости.Замечание: При решении задачи «Пересекает ли отрезок плоскость» достаточно подставить координаты этих точек в заданное уравнение плоскости (не обязательно нормированное!), чтобы установить:пересекает плоскость, если вычисленные значения правой части уравнения плоскости имеют разные знаки;не пересекает плоскость, если знаки совпадают.

1. Рассмотрим вектор с проекциями на координатные оси, соответственно равнымиA, B и C, т. е. .

2. Возьмем на плоскости Ax + By + Cz + D = 0 две произвольные точки M(x₁, y₁, z₁) и N(x₂, y₂, z₂) и рассмотрим вектор . Этот вектор лежит в плоскостиAx + By + Cz + D = 0. Его проекции на координатные оси соответственно равны x₂ - x₁, y₂ - y₁, z₂ - z₁ и .

3. Так как точки M и N лежат в плоскости Ax + By + Cz + D = 0, то имеют место равенства

Ax₁ + By₁ + Cz₁ + D = 0

и

Ax₂ + By₂ + Cz₂ + D = 0.

Вычитая первое уравнение из второго, получим

A(x₂ - x₁) + B(y₂ - y₁) + C(z₂ - z₁) = 0.     (1)

Скалярное произведение вектора на векторравно

A(x₂ - x₁) + B(y₂ - y₁) + C(z₂ - z₁).

Так как на основании (1) это скалярное произведение равно нулю, то вектор перпендикулярен вектору, а тем самым и той плоскости, в которой лежит этот вектор, т. е. векторперпендикулярен плоскостиAx + By + Cz + D = 0.

Геометрическое значение коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0 состоит в том, что они являются проекциями на координатные оси Ox, Oy, Oz вектора, перпендикулярного этой плоскости.