9.3. Преобразования Лоренца для координат и времени

Формулы преобразования координат, при переходе из одной системы отсчета в другую, в теории относительности называют преобразованиями Лоренца.

Для получения преобразований Лоренца выберем две инерциальные системы отсчета К и К^'. Предположим, что система К^' движется равномерно и прямолинейно относительно системы К со скоростью v. В начальный момент времени системы К и К^' совпадали. Для любого другого момента времени расположение координатных осей систем сохраняется. При этом любая точка имеет одни и те же координаты у, z и у^', z^'. Координаты x и t связаны функционально: x = f(x^', t^'); t = F(x^', t^').

Таким образом, формулы преобразования координат можно записать в виде

x = f(x^', t^'); у = у^'; z = z^'; t = F(x^', t^'). (9.16)

Формулы преобразования координат не должны изменять интервал между двумя событиями в силу его инвариантности, что возможно в том случае, когда выбранные системы отсчета равномерно вращаются относительно начала координат и относительно друг друга. В силу начальных условий положение точки М в каждой из систем отсчета может быт определено координатами М(x,) и М(x^',τ^') (рис.9.2).

Из рисунка видно, что координата

x = OA = ОВ - АВ = ОВ - МС^'. OB = x^'cos;

MC^' = τ^'sin ( MC^'B^'); τ = AM = AA^' + A^'M;

AA^' = OC = τ^'cosφ; A^'M = x^'sinφ.

Следовательно, формулы преобразования координат принимают вид

x = x^'cosφ - τ^'sinφ; у = у^';

z = z^'; τ = τ^'cosφ + x^'sinφ. (9.17)

Для точек, совпадающих с началом координат (O; O^'), имеем

x = vt; τ = ict; x^' = 0; τ^' = ict^'.

Подставляя значения x , τ, x^', τ^' в формулы преобразования, получим

x = - τ^'sinφ; τ = τ^'cosφ.

Разделив x на τ, имеем

. (9.18)

Из тригонометрических соображений

; .

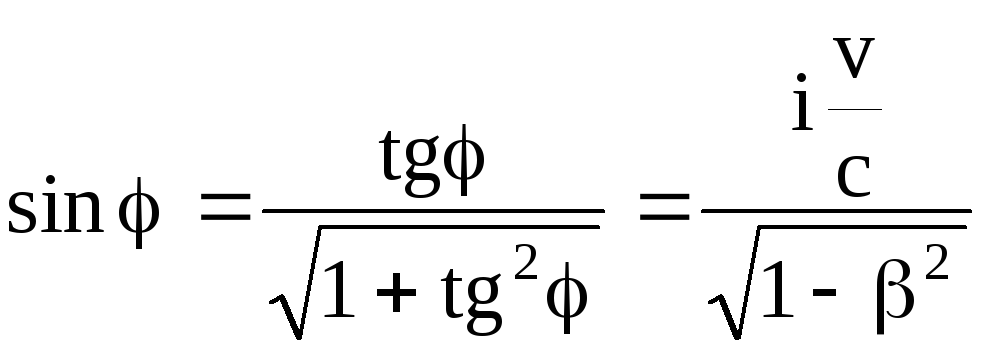Подставляя значения sinφ и cosφ в формулы преобразований с учетом τ=ict, τ^' = ict^', будем иметь

; у = у^'; z = z^'; . (9.19)

Полученные соотношения называют обратными преобразованиями Лоренца.

Прямые преобразования Лоренца:

; у = у^'; z = z^'; . (9.20)

9.4. Следствия из преобразований Лоренца

9.4.1. Закон сложения скоростей в теории относительности

Для вывода закона сложения скоростей в теории относительности воспользуемся прямыми преобразованиями Лоренца (9.20):

; у = у^'; z = z^'; .

Дифференцируя левые и правые части написанных формул, получим

; dу = dу^'; dz = dz^'; . (9.21)

Деля, почленно, левые и правые части первых трех равенств на левую и правую части четвертого равенства, будем иметь

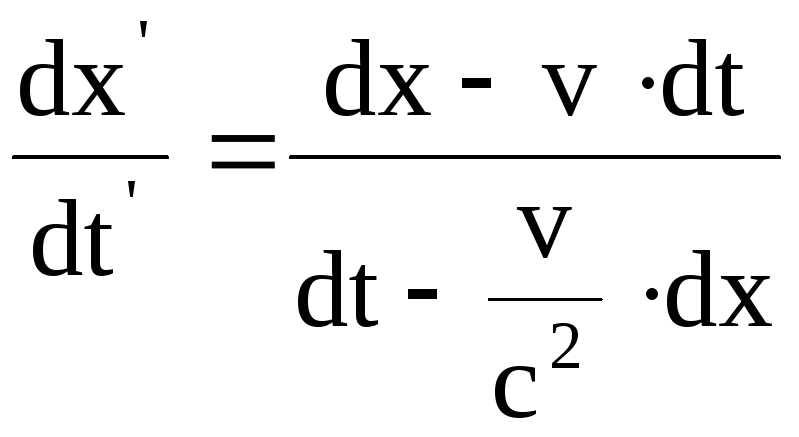; ; . (9.22)

Если скорости тела в системе К u_x = dx/dt; u_у = dy/dt; u_z = dz/dt, а в системе К^' u_x^' = dx^'/dt^'; u_у^' = dy^'/dt^'; u_z^' = dz^'/dt^', то закон сложения скоростей в теории относительности имеет вид

; ; . (9.23)

Вводя угол  между скоростью u и направлением оси OX, для абсолютной величины скорости (u^')² = (u_x^')² + (u_y^')² + (u_z^')² получим

. (9.24)

В частном случае, когда скорость u направлена вдоль оси OX, формула сложения скоростей в теории относительности принимает вид

. (9.25)

Из формулы (9.25) видно, что при малых скоростях (uc и vc) формула сложения скоростей в теории относительности переходит в формулу сложения скоростей в классической механике.

Из закона сложения скоростей в теории относительности можно установить, в чем заключалась ошибка в рассуждениях Максвелла (а следовательно, и в попытках понять отрицательный результат опыта Майкельсона). Кроме того, из него можно установить, что действительно величина скорости распространения света в вакууме абсолютна, одинакова во всех системах отсчета. Так, при подстановке в (9.25) u = c или v = c нетрудно определить, что u^' = c.

Заметим, что если обе складываемые скорости меньше скорости распространения света в вакууме, то и суммарная скорость тоже оказывается меньше c.

Действительно, пусть u = c(1-), v = - c(1-), где 0 и 0. Тогда классический закон сложения скоростей дал бы (в случае, когда скорость тела u направлена вдоль оси OX) для скорости тела в системе К^' u^'=u-v=c(2--)c.

Закон сложения скоростей в теории относительности приводит к следующему результату:

с. (9.26)

Это еще раз подтверждает, что скорость распространения света в вакууме  предельная скорость распространения любого сигнала (любой скорости движения материальной точки, тела, частицы).

Следует отметить, что инвариантной по отношению к преобразованиям Лоренца является только абсолютная величина скорости света в вакууме, но не ее направление.