
- •В.М. Полунин, г.Т.Сычев
- •Физические основы механики
- •Конспект лекций
- •Содержание
- •От авторов
- •Лекция 1. Вводная
- •Лекция 2. Элементы кинематики
- •2.1. Механика и ее разделы. Физические модели: материальная точка (частица), абсолютно твердое тело (система материальных точек), сплошная среда
- •2.2. Пространственно-временные отношения. Развитие представлений о свойствах пространства и времени в механике
- •2.3. Системы отсчета и описание движений. Элементы кинематики материальной точки: перемещение, скорость и ускорение
- •2.4. Элементы кинематики материальной точки и тела, совершающих вращательное движение: угол поворота, угловые скорость и ускорение. Их связь с линейной скоростью и линейным ускорением
- •2.5. Гармонические колебательные движения и их характеристики: смещение, амплитуда, период, частота, фаза, скорость и ускорение
- •2.6. Методы сложения гармонических колебаний. Векторные диаграммы. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения
- •2.7. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу
- •Лекция 3.Элементы динамики материальной точки и твердого тела
- •3.2. Инерциальные и неинерциальные системы отсчета
- •3.3. Описание движения в неинерциальных системах отсчета
- •3.3.1. Силы инерции при ускоренном движении системы отсчета
- •3.3.2. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета
- •3.3.3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета (сила Кориолиса)
- •Силы инерции, возникающие в неинерциальной системе отсчета в зависимости от состояния частицы
- •3.5. Основной закон динамики вращательного движения
- •3.6. Сопоставление формул динамики вращательного и динамики поступательного движений
- •Сопоставление формул динамики поступательного движения и динамики вращательного движения
- •Лекция 4. Физика колебаний. Гармонический осциллятор. Нормальные моды
- •4.1. Дифференциальное уравнение гармонических колебаний и его решение
- •4.2. Примеры гармонических осцилляторов. Физический, математический и пружинный маятники. Определение их периодов и частот
- •4.2.1. Пружинный маятник
- •4.2.2. Физический и математический маятники
- •4.3. Свободные (затухающие колебания). Дифференциальное уравнение затухающих колебаний и его решение. Характеристики затухающих колебаний
- •4.4. Вынужденные колебания гармонического осциллятора под действием синусоидальной силы. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний
- •Лекция 5.Ангармонические колебания
- •5.1. Нелинейный осциллятор. Физические системы, содержащие нелинейность
- •5.2. Автоколебания. Обратная связь. Условие самовозбуждения. Роль нелинейности. Предельные циклы
- •Лекция 6. Физика волн. Волновые процессы
- •6.1. Кинематика и динамика волновых процессов. Плоская стационарная и синусоидальная волна
- •6.2. Уравнение плоской волны
- •6.3.Волновое уравнение
- •6.4. Интерференция волн. Стоячие волны
- •Лекция 7.Энергия, работа, мощность
- •7.1. Работа силы и её выражение через криволинейный интеграл
- •Из (7.1) следует, что при
- •7.1.1. Работа, совершаемая внешними силами при вращательном движении относительно неподвижной оси
- •7.2. Мощность
- •Различают мгновенную мощность и среднюю мощность.
- •Поскольку
- •7.3. Энергия как универсальная мера различных форм движений и взаимодействий
- •7.4. Кинетическая энергия системы и её связь с работой внешних и внутренних сил, приложенных к системе
- •7.5. Энергия системы, совершающей вращательное движение
- •Подставив значение VI в (7.35) будем иметь
- •То есть работа внешних сил, действующих на вращающуюся относительно неподвижной оси материальную точку (тело, систему), равна изменению кинетической энергии:
- •7.6. Потенциальная энергия и энергия взаимодействия. Потенциальная энергия и устойчивость системы
- •7.6.1. Связь между потенциальной энергией и силой
- •7.6.2. Внутренняя энергия
- •7.6.3. Силовые поля. Поле как форма существования материи. Поле как форма существования материи осуществляющая силовое взаимодействие между материальными объектами. Характеристики силовых полей
- •Второй характеристикой силового потенциального поля является потенциал.
- •7.6.4. Потенциальная энергия материальной точки (тела, системы) во внешнем силовом поле
- •7.6.5. Поле центральных сил. Движение в поле центральных сил
- •Элементарная работа по перемещению массы на элементарном отрезке dr:
- •Из полученного соотношения видно:
- •В случае, когда сила притяжения будет равна центростремительной силе, то
- •Подставляя значения vа и vп в формулу (7.41), будем иметь
- •Подставив в формулу (7.83) значения r и V, будем иметь t 92 мин.
- •7.7. Энергия упругой деформации
- •7.8. Энергия системы, совершающей колебательное движение
- •Кинетическая энергия системы, совершающей гармоническое колебание, находится по формуле
- •Лекция 8. Законы сохранения в механике
- •8.1. Закон сохранения энергии в механике
- •8.1.1. Общефизический закон сохранения энергии
- •8.1.2. Закон сохранения и превращения механической энергии
- •8.2. Закон сохранения импульса. Центр инерции. Закон движения центра инерции
- •8.3. Закон сохранения момента импульса. Уравнение моментов
- •В векторной форме
- •8.4. Применение законов сохранения к упругому и неупругому взаимодействиям (удару)
- •8.4.1. Абсолютно неупругий удар шаров
- •Лекция 9. Основы релятивистской механики. Релятивистская кинематика
- •9.1. Принцип относительности Галилея. Преобразования Галилея. Инварианты преобразования. Закон сложения скоростей в классической механике
- •9.2. Постулаты и представления о свойствах пространства и времени в специальной теории относительности
- •9.3. Преобразования Лоренца для координат и времени
- •9.4. Следствия из преобразований Лоренца
- •9.4.1. Закон сложения скоростей в теории относительности
- •9.4.2. Сокращение движущихся масштабов длин
- •9.4.3.Замедление хода движущихся часов
- •Лекция 10.Релятивистская динамика
- •10.2. Четырехмерное пространство - время. Преобразования в четырехмерном пространстве
- •10.2.1. Основные понятия
- •10.2.2. Кинематика четырехмерного пространства-времени
- •10.2.3. Динамика четырехмерного пространства-времени
- •10.3. Столкновения релятивистских частиц. Законы сохранения энергии и импульса
- •10.4. Значение теории относительности
- •Библиографический список Основной
- •Дополнительный
- •Физика Физические основы механики Конспект лекций
2.2. Пространственно-временные отношения. Развитие представлений о свойствах пространства и времени в механике
Пространство и время – категории, обозначающие основные формы существования и взаимодействия объектов.
Пространство выражает порядок существования объектов. Время - порядок смены событий.
Пространство и время - основные понятия всех разделов физики. Они играют важную роль на эмпирическом уровне физического познания. Непосредственное содержание результатов наблюдений и экспериментов состоит в фиксации пространственно - временных совпадений. Они служат также одними из важнейших средств конструирования теоретических моделей, интерпретирующих экспериментальные данные.
Для построения физической картины мира понятия пространство и время, обеспечивая отождествление и различие (индивидуализацию) отдельных фрагментов материальной действительности, имеют решающее значение.
Различают метрические (протяженность и длительность) и топологические (размерность, непрерывность и связанность, порядок и направление времени) свойства пространства и времени.
Современными теориями метрических свойств пространства и времени являются: специальная теория относительности (СТО) и общая теория относительности (ОТО).
Исследование топологических свойств пространства и времени в физике было начато в 60 - 70-х годах двадцатого столетия и пока не вышло из стадии гипотез.
Историческое развитие физических представлений о пространстве и времени проходило по двум направлениям в тесной связи с различными философскими представлениями.
В основе одного из них лежали идеи Демокрита, приписывающие пустоте особый род бытия. Они нашли наиболее полное физическое воплощение в понятиях абсолютного пространства и времени И. Ньютона. Согласно И. Ньютону абсолютное пространство и время представляют собой самостоятельные сущности, которые не зависят друг от друга, и от находящихся в них материальных объектов и протекающих в них процессов.
Другое представление о пространстве и времени заложено в учении Аристотеля, которое было разработано в философских работах Г.В. Лейбница, трактовавшего пространство и время как определенные типы отношений между объектами и их изменениями, не имеющие самостоятельного существования. В физике концепция Г.В. Лейбница была развита А. Эйнштейном в теории относительности.
2.3. Системы отсчета и описание движений. Элементы кинематики материальной точки: перемещение, скорость и ускорение
Известно, что кинематика - это учение о геометрических свойствах движения и взаимодействия тел, или раздел механики, в котором изучаются движения и взаимодействия тел в не связи с причинами, их порождающими. Изучается простейший вид движения - механическое движение. Это процесс изменения положения физических тел или их частей по отношению к другим телам или частям одного и того же тела в пространстве и во времени. Поэтому механическое движение всегда относительно.
Произвольно выбранное, условно неподвижное тело, по отношению к которому рассматривается движение данного тела, называют телом отсчета.
Связанная с телом отсчета произвольная система координат называется системой отсчета.
Рис.2.1

На рис. 2.1 показана прямоугольная (декартова) система координат.
Положение материальной точки (тела) в прямоугольной системе отсчета, в данный момент времени, может быть определено тремя способами: 1) с помощью координат x, y, z - M(x,y,z). В этом случае говорят, что материальная точка обладает тремя степенями свободы; 2) с помощью радиус - вектора r; 3) естественным (траекторным), который применяется обычно тогда, когда известна траектория движения точки по отношению к выбранной системе отсчета. В этом случае зависимость S = f(t) может быть задана графически либо в виде таблицы. При этом указанные способы равноправны.
Между координатами x, y, z и проекциями радиус-вектора r существует связь:
x
= rx,
y = ry,
z = rz. ![]() (2.1)
(2.1)
С течением времени может произойти изменение положения материальной точки (тела) в пространстве (изменение ее координат), тогда можно записать:
x = f1(t); y = f2(t); z = f3(t); (2.2)
rx = f1(t); ry = f2 (t); rz = f3(t). (2.3)
Записанные выражения являются уравнениями движения материальной точки (тела) в кинематике.
Совокупность последовательных положений материальной точки (тела) в процессе ее движения называют траекторией движения. Для определения (нахождения) уравнения траектории движения необходимо из уравнений движения исключить время.
Положение
материальной точки в полярной системе
координат задается радиус-вектором
![]() ,
который имеет определенный модуль r, и
углами
и ,
которые он составляет с осями декартовой
системы координат.
,
который имеет определенный модуль r, и
углами
и ,
которые он составляет с осями декартовой
системы координат.
С точки зрения кинематики, никакого различия между различными системами отсчета нет, и все они равноправны.
Простейшим видом механического движения тела является поступательное движение. Это такое движение, при котором тело перемещается параллельно самому себе. При этом все точки тела описывают одинаковые траектории, смещенные относительно друг друга. Рассматривая движение отдельных точек, можно установить характер движения тела.
Для характеристики движения материальной точки вводятся следующие основные понятия и определения.
Перемещение - вектор, проведенный из начального положения материальной точки (тела) в ее положение в данный момент времени (отрезок, соединяющий последовательные положения материальной точки или тела) - приращение радиус-вектора r за рассматриваемый промежуток времени
r = r – rо. (2.4)
Рис.2.2

![]() – вектор перемещения точки за промежуток
времениt:
– вектор перемещения точки за промежуток
времениt:
![]() или
или
![]() ;
S
– пройденный за это время путь.
;
S
– пройденный за это время путь.
В общем случае перемещение не совпадает с траекторией движения. Достаточно малое перемещение, которое с достаточной степенью точности совпадает с соответствующим участком траектории движения, называют элементарным перемещением - dr.
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения численно равен пройденному пути:
r = S (2.5)
Расстояние - модуль перемещения. Расстояние, пройденное телом при его движении по траектории, - путь. В частных случаях перемещение и путь могут совпадать.
За одни и те же промежутки времени перемещение точки может быть разным. Если положение точки в пространстве в какой-то момент времени t определить вектором r(t), а в момент времени t + t - (r + r), то за время (t2 – t1) = t она совершает перемещение r. При этом отношение r/t зависит от t. Однако при уменьшении t эта зависимость становится менее явной, и при t0 оно стремится к некоторому пределу. Предел отношения r/t при t0 называют мгновенной скоростью.
Таким образом, мгновенная линейная скорость - векторная физическая величина, характеризующая состояние движения, показывающая, как изменяется перемещение в единицу времени, численно равная первой производной от перемещения по времени:
![]() (2.6)
(2.6)
Скоростью определяется как "быстрота" движения, так и его направление. При неравномерном движении модуль мгновенной скорости с течением времени может изменяться. В этом случае пользуются понятием средней скорости движения.
Средняя скорость неравномерного движения - скалярная физическая величина, численно равная отношению всего пути, пройденного телом (материальной точкой), к тому промежутку времени, в течение которого совершалось движение:
![]() (2.7)
(2.7)
Важной задачей кинематики является нахождение пройденного материальной точкой пути. Известно, что при прямолинейном равнопеременном движении
![]() .
Согласно (2.6),
.
Согласно (2.6),
![]() ,
следовательно
,
следовательно
dS = vdt. (2.8)
При небольших промежутках времени t можно считать, что элементарный путь dS численно равен dr, причем при уменьшении промежутка времени точность совпадения числовых значений пути и перемещения возрастает.
Рис.2.3

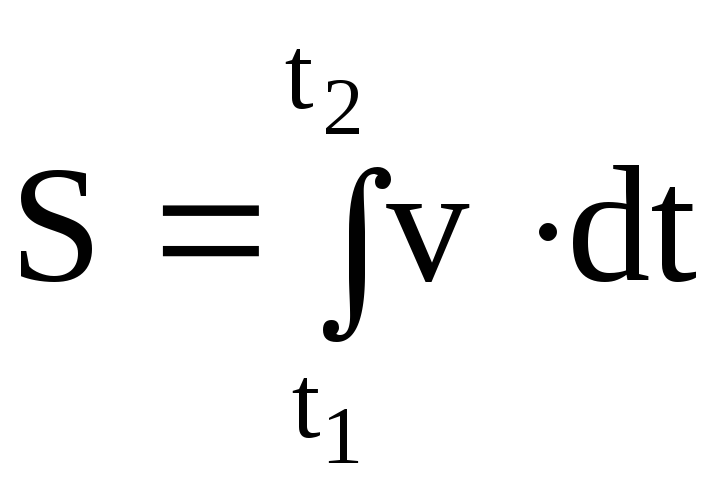 .
(2.9)
.
(2.9)
Таким образом, величина пути определяется криволинейным интегралом.
Это дает право представлять величину пройденного телом пути площадью фигуры, ограниченной кривой зависимости v = f(t), прямыми t = t1,
t = t2 и осью времени на графике скорости (рис.2.3).
В
общем случае найти
уравнение пути
- означает определить зависимость
координат от времени:
![]() При
движении скорость материальной точки
(тела) может изменяться как по величине,
так и по направлению. Отношение изменения
скоростиv
к промежутку времени t,
в течение которого оно происходит,
зависит от величины t,
однако при его уменьшении эта зависимость
становится менее явной, и при t0
оно стремится к пределу, который называют
линейным
ускорением:
При
движении скорость материальной точки
(тела) может изменяться как по величине,
так и по направлению. Отношение изменения
скоростиv
к промежутку времени t,
в течение которого оно происходит,
зависит от величины t,
однако при его уменьшении эта зависимость
становится менее явной, и при t0
оно стремится к пределу, который называют
линейным
ускорением:
![]() . (2.10)
. (2.10)
Следовательно, линейное ускорение - векторная физическая величина, характеризующая изменение скорости в единицу времени, численно равная первой производной от скорости или второй производной от перемещения по времени.
В общем случае вектор линейного ускорения не совпадает с вектором линейной скорости. Можно разложить вектор линейного ускорения на две составляющие по направлению линейной скорости - вдоль касательной к траектории движения. Эту составляющую линейного ускорения называют тангенциальным ускорением – аt. Тангенциальное ускорение изменяет линейную скорость только по величине:
![]() .
(2.11)
.
(2.11)
Составляющую линейного ускорения, направленную по нормали n к вектору линейной скорости, т.е. к касательной в данной точке, называют нормальным ускорением - an. Нормальное ускорение изменяет линейную скорость только по направлению:
![]() ,
,
![]() (2.12)
(2.12)
где R - радиус кривизны траектории движения;
n - единичный вектор нормали к траектории движения.
Полное ускорение a можно определить как
![]() .
(2.13)
.
(2.13)
Таким образом, направление тангенциального ускорения всегда совпадает с направлением линейной скорости, а направление нормального ускорения перпендикулярно направлению линейной скорости.
При неравномерном движении величину
![]() (2.14)
(2.14)
называют мгновенным ускорением, а
![]() (2.15)
(2.15)
-средним ускорением.
Надо отметить, что при поступательном движении тела все его точки имеют одинаковые линейные скорости и ускорения и описывают одинаковые траектории, смещенные относительно друг друга.
