
- •В.М. Полунин, г.Т.Сычев
- •Физические основы механики
- •Конспект лекций
- •Содержание
- •От авторов
- •Лекция 1. Вводная
- •Лекция 2. Элементы кинематики
- •2.1. Механика и ее разделы. Физические модели: материальная точка (частица), абсолютно твердое тело (система материальных точек), сплошная среда
- •2.2. Пространственно-временные отношения. Развитие представлений о свойствах пространства и времени в механике
- •2.3. Системы отсчета и описание движений. Элементы кинематики материальной точки: перемещение, скорость и ускорение
- •2.4. Элементы кинематики материальной точки и тела, совершающих вращательное движение: угол поворота, угловые скорость и ускорение. Их связь с линейной скоростью и линейным ускорением
- •2.5. Гармонические колебательные движения и их характеристики: смещение, амплитуда, период, частота, фаза, скорость и ускорение
- •2.6. Методы сложения гармонических колебаний. Векторные диаграммы. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения
- •2.7. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу
- •Лекция 3.Элементы динамики материальной точки и твердого тела
- •3.2. Инерциальные и неинерциальные системы отсчета
- •3.3. Описание движения в неинерциальных системах отсчета
- •3.3.1. Силы инерции при ускоренном движении системы отсчета
- •3.3.2. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета
- •3.3.3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета (сила Кориолиса)
- •Силы инерции, возникающие в неинерциальной системе отсчета в зависимости от состояния частицы
- •3.5. Основной закон динамики вращательного движения
- •3.6. Сопоставление формул динамики вращательного и динамики поступательного движений
- •Сопоставление формул динамики поступательного движения и динамики вращательного движения
- •Лекция 4. Физика колебаний. Гармонический осциллятор. Нормальные моды
- •4.1. Дифференциальное уравнение гармонических колебаний и его решение
- •4.2. Примеры гармонических осцилляторов. Физический, математический и пружинный маятники. Определение их периодов и частот
- •4.2.1. Пружинный маятник
- •4.2.2. Физический и математический маятники
- •4.3. Свободные (затухающие колебания). Дифференциальное уравнение затухающих колебаний и его решение. Характеристики затухающих колебаний
- •4.4. Вынужденные колебания гармонического осциллятора под действием синусоидальной силы. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний
- •Лекция 5.Ангармонические колебания
- •5.1. Нелинейный осциллятор. Физические системы, содержащие нелинейность
- •5.2. Автоколебания. Обратная связь. Условие самовозбуждения. Роль нелинейности. Предельные циклы
- •Лекция 6. Физика волн. Волновые процессы
- •6.1. Кинематика и динамика волновых процессов. Плоская стационарная и синусоидальная волна
- •6.2. Уравнение плоской волны
- •6.3.Волновое уравнение
- •6.4. Интерференция волн. Стоячие волны
- •Лекция 7.Энергия, работа, мощность
- •7.1. Работа силы и её выражение через криволинейный интеграл
- •Из (7.1) следует, что при
- •7.1.1. Работа, совершаемая внешними силами при вращательном движении относительно неподвижной оси
- •7.2. Мощность
- •Различают мгновенную мощность и среднюю мощность.
- •Поскольку
- •7.3. Энергия как универсальная мера различных форм движений и взаимодействий
- •7.4. Кинетическая энергия системы и её связь с работой внешних и внутренних сил, приложенных к системе
- •7.5. Энергия системы, совершающей вращательное движение
- •Подставив значение VI в (7.35) будем иметь
- •То есть работа внешних сил, действующих на вращающуюся относительно неподвижной оси материальную точку (тело, систему), равна изменению кинетической энергии:
- •7.6. Потенциальная энергия и энергия взаимодействия. Потенциальная энергия и устойчивость системы
- •7.6.1. Связь между потенциальной энергией и силой
- •7.6.2. Внутренняя энергия
- •7.6.3. Силовые поля. Поле как форма существования материи. Поле как форма существования материи осуществляющая силовое взаимодействие между материальными объектами. Характеристики силовых полей
- •Второй характеристикой силового потенциального поля является потенциал.
- •7.6.4. Потенциальная энергия материальной точки (тела, системы) во внешнем силовом поле
- •7.6.5. Поле центральных сил. Движение в поле центральных сил
- •Элементарная работа по перемещению массы на элементарном отрезке dr:
- •Из полученного соотношения видно:
- •В случае, когда сила притяжения будет равна центростремительной силе, то
- •Подставляя значения vа и vп в формулу (7.41), будем иметь
- •Подставив в формулу (7.83) значения r и V, будем иметь t 92 мин.
- •7.7. Энергия упругой деформации
- •7.8. Энергия системы, совершающей колебательное движение
- •Кинетическая энергия системы, совершающей гармоническое колебание, находится по формуле
- •Лекция 8. Законы сохранения в механике
- •8.1. Закон сохранения энергии в механике
- •8.1.1. Общефизический закон сохранения энергии
- •8.1.2. Закон сохранения и превращения механической энергии
- •8.2. Закон сохранения импульса. Центр инерции. Закон движения центра инерции
- •8.3. Закон сохранения момента импульса. Уравнение моментов
- •В векторной форме
- •8.4. Применение законов сохранения к упругому и неупругому взаимодействиям (удару)
- •8.4.1. Абсолютно неупругий удар шаров
- •Лекция 9. Основы релятивистской механики. Релятивистская кинематика
- •9.1. Принцип относительности Галилея. Преобразования Галилея. Инварианты преобразования. Закон сложения скоростей в классической механике
- •9.2. Постулаты и представления о свойствах пространства и времени в специальной теории относительности
- •9.3. Преобразования Лоренца для координат и времени
- •9.4. Следствия из преобразований Лоренца
- •9.4.1. Закон сложения скоростей в теории относительности
- •9.4.2. Сокращение движущихся масштабов длин
- •9.4.3.Замедление хода движущихся часов
- •Лекция 10.Релятивистская динамика
- •10.2. Четырехмерное пространство - время. Преобразования в четырехмерном пространстве
- •10.2.1. Основные понятия
- •10.2.2. Кинематика четырехмерного пространства-времени
- •10.2.3. Динамика четырехмерного пространства-времени
- •10.3. Столкновения релятивистских частиц. Законы сохранения энергии и импульса
- •10.4. Значение теории относительности
- •Библиографический список Основной
- •Дополнительный
- •Физика Физические основы механики Конспект лекций
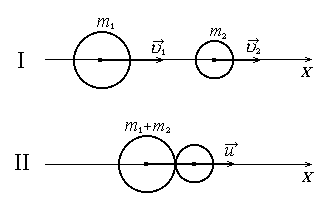
8.4.1. Абсолютно неупругий удар шаров
Абсолютно неупругий удар шаров (тел) характеризуется тем, что кинетическая энергия системы (шаров) полностью или частично превращается во внутреннюю энергию. Это означает, что для замкнутой системы не выполняется закон сохранения механической энергии, а выполняется только закон сохранения импульса. Шары (тела) после такого взаимодействия либо движутся с одинаковой скоростью, либо покоятся.
Рис.8.2
![]() . (8.41)
. (8.41)
Откуда
![]() .
(8.42)
.
(8.42)
Подсчитаем потерю системой кинетической энергии:
 =
=
![]() .
(8.43)
.
(8.43)
Интересен
случай, когда
![]() ,
,![]() .
Формула (8.43) в таком случае преобразуется
к виду
.
Формула (8.43) в таком случае преобразуется
к виду
![]() .
(8.44)
.
(8.44)
Таким
образом, потери кинетической энергии
составляют
![]() .
.
Если
же
![]() ,
то потери энергии
,
то потери энергии
![]() . (8.45)
. (8.45)
Рис.8.3

Рассмотрим
абсолютно упругий удар шаров, при
котором происходит упругая деформация
шаров, не возникает тепла и пластической
деформации (рис.8.3). Даны массы шаров и
их скорости до удара
![]() ,
,
![]() .
В результате такого взаимодействия
вся кинетическая энергия до удара
превращается в кинетическую энергию
системы (шаров) после удара. В результате
после удара шары будут двигаться с
некоторыми скоростями u1
и u2.
.
В результате такого взаимодействия
вся кинетическая энергия до удара
превращается в кинетическую энергию
системы (шаров) после удара. В результате
после удара шары будут двигаться с
некоторыми скоростями u1
и u2.
Пусть
![]() .
Шары взаимодействуют только между
собой, т.е. система замкнута, между
телами действуют только консервативные
силы.
.
Шары взаимодействуют только между
собой, т.е. система замкнута, между
телами действуют только консервативные
силы.
В такой ситуации должны выполняться законы сохранения импульса и механической энергии. Запишем эти законы применительно к данному случаю, причем закон сохранения импульса представим в алгебраической форме:
 .
(8.46)
.
(8.46)
Перепишем эти формулы следующим образом:
![]() ;
(8.47)
;
(8.47)
![]() .
(8.48)
.
(8.48)
Разделим (8.48) на (8.47) почленно:
![]() . (8.49)
. (8.49)
Теперь
имеем систему линейных уравнений (8.47)
и (8.49). Для нахождения скоростей шаров
после взаимодействия
![]() ,
,![]() выразим из (8.49)
выразим из (8.49)![]() и подставим в (8.47):
и подставим в (8.47):
![]() ,
,
![]()
![]() .
.
Откуда
![]() .
(8.50)
.
(8.50)
В
системе уравнений (8.46) ничего не
изменится, если заменить индекс 1 на
индекс 2, поэтому для получения формулы,
выражающей
![]() ,
достаточно в формуле (8.50) заменить
индекс 1 на индекс 2:
,
достаточно в формуле (8.50) заменить
индекс 1 на индекс 2:
![]() .
(8.51)
.
(8.51)
В общем случае
![]() ;
(8.52)
;
(8.52)
![]() .
(8.53)
.
(8.53)
Знак (+) соответствует случаю, когда первый шар нагоняет второй, а знак (-) - когда шары движутся навстречу друг другу.
Из уравнения (8.53) видно, что:
1) если m1 = m2 = m, то u1 = v2, а u2 = v1, т.е. в этом случае шары обмениваются скоростями;
2) при ударе шара о стенку (m2>>m1):
а) u2 = v2 - скорость стенки остается неизменной;
б) u1 = 2v2 – v1 - при этом, если стенка неподвижна (v2 = 0), скорость шара после удара, оставаясь неизменной по величине, изменяет свое направление на противоположное. При v2 = 0 u1 возрастает до 2v2 при движении стенки навстречу шару и убывает до 2v2, если стенка удаляется от него.
