Лекция 7.Энергия, работа, мощность

Работа силы и её выражение через криволинейный интеграл. Мощность. Энергия как универсальная мера различных форм движений и взаимодействий. Кинетическая энергия системы и её связь с работой внешних и внутренних сил, приложенных к системе. Энергия системы, совершающей вращательное движение. Энергия системы, совершающей колебательное движение. Потенциальная энергия и энергия взаимодействия. Потенциальная энергия тела, находящегося в поле тяготения другого тела. Потенциальная энергия и устойчивость системы. Внутренняя энергия. Энергия упругой деформации.

7.1. Работа силы и её выражение через криволинейный интеграл

Работа - это изменение формы движения, рассматриваемое с его количественной стороны. В общем смысле работа - это процесс превращения одних форм движения материи в другие и одновременно количественная характеристика этого процесса.

Механическая работа - процесс, в котором под действием сил изменяется энергия системы, и одновременно количественная мера этого изменения.

При совершении работы всегда имеются сила, действующая на материальную точку (систему, тело), и вызванное данной силой перемещение. При отсутствии хотя бы одного из этих факторов работа не совершается.

Элементарная работа некоторой силы F, действующей на материальную точку (тело, систему), вызывающей элементарное перемещение dr, равна произведению силы на перемещение:

dA = Fdr = Fdrcos = F_rdr, (7.1)

где α - угол между направлением перемещения и направлением действующей силы.

Из (7.1) следует, что при

α < π/2, dA > 0 - работа положительная;

α = π/2, dA = 0 - работа не совершается;

α > π/2, dA < 0 - работа отрицательная;

α = 0, dA = Fdr - направление перемещения и направление действующей силы совпадают.

В том случае, когда величина тангенциальной составляющей силы остаётся всё время неизменной, то работа определяется соотношением

. (7.2)

В частности, это условие выполняется, если тело движется прямолинейно, и постоянная по величине сила образует с направлением движения постоянный угол. Поэтому выражению (7.2) в данном случае можно придать следующий вид:

. (7.3)

Надо отметить, что понятие работы в механике существенно отличается от обыденного представления о работе. Например, для того, чтобы держать тяжелый груз, стоя неподвижно, а тем более для того, чтобы перенести этот груз по горизонтальному пути, носильщик затрачивает определенные усилия, т.е. "совершает работу". Однако работа как механическая величина в этих случаях равна нулю.

Вектор силы на плоскости всегда можно разложить на две составляющие - нормальную и тангенциальную. Ясно, что только тангенциальная составляющая силы способна совершить работу. В случае, когда величина проекции силы на направление перемещения не остается постоянной во времени, для вычисления работы следует разбить путь S на элементарные участки , взяв их столь малыми, что за время прохождения телом такого участка можно было бы считать силу постоянной. Тогда на каждом элементарном участке путиS₁работа силы равна

. (7.4)

А работа на всем пути S может быть вычислена как сумма элементарных работ:

. (7.5)

В общем случае, когда материальная точка (тело, система), двигаясь по криволинейной траектории, проходит путь конечной длины, можно мысленно разбить этот путь на бесконечно малые элементы, на каждом из которых сила F может считаться постоянной, а элементарная работа может быть вычислена по формуле (7.1). Сложив все эти элементарные работы и перейти к пределу, устремив к нулю длины всех элементарных перемещений, а их число – к бесконечности, получим

. (7.6)

Выражение (7.6) называют криволинейным интегралом вектора F вдоль траектории L.

Рис.7.1

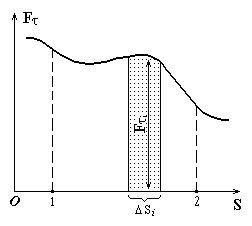
Работу, определяемую формулой (7.6), можно изобразить графически, в координатах F - S, площадью фигуры, что соответствует нахождению криволинейного интеграла. На рис.7.1 построен график F_ как функции положения точки на траектории. Из рисунка видно, что элементарная работа численно равна площади заштрихованной полоски, а работана пути от точки 1 до точки 2 численно равна площади фигуры, ограниченной кривой F_(S), вертикальными прямыми 1 и 2 и осью OS.

Единица измерения работы в СИ носит название джоуль (Дж).

Найдем работу, совершаемую при растяжении пружины, подчиняющемуся закону Гука. Сила, растягивающая пружину, равна по величине и противоположна по направлению упругой силе, т.е.

, (7.7)

где – удлинение пружины.

Сила действует в направлении перемещения, поэтому

. (7.8)

Элементарная работа в данном случае может быть представлена в виде

. (7.9)

По формуле (7.6) найдем полную работу:

. (7.10)

При сжатии пружины на величину совершается такая же по величине и знаку работа, как и при растяжении.

Экспериментально установлено, что работа сил тяжести, упругих сил, электрических сил не зависит от формы траектории, а определяется начальным и конечным положениями материальной точки (системы, тела). Работа этих сил по замкнутой траектории равна нулю:

. (7.11)

Силы, для которых выполняется данное условие, называются консервативными или потенциальными.

Работа консервативных сил на любом замкнутом пути равна нулю. Поэтому потенциальное поле сил можно определить как поле таких сил, работа которых на любом замкнутом пути равна нулю. Поскольку работа в потенциальном поле сил на замкнутом пути равна нулю, то на одних участках замкнутого пути силы совершают положительную работу, а на других – отрицательную.

Все силы, не удовлетворяющие этому условию, называются неконсервативными.