4.3. Свободные (затухающие колебания). Дифференциальное уравнение затухающих колебаний и его решение. Характеристики затухающих колебаний

Колебательные движения реальной колебательной системы всегда сопровождаются силами трения и сопротивления, которые приводят к уменьшению амплитуды колебаний. Если энергия, потерянная системой, не восполняется за счет внешних сил, то колебания системы называются затухающими, свободными или собственными.

В линейных системах свободные колебания представляют собой суперпозицию нормальных колебаний (нормальных мод).

Рис.4.4

Cделаем существенное приближение к действительности, если учтем наличие силы сопротивления (трения) , т.е. учтем диссипадию энергии колебательной системы. Предположим, что сила трения обусловлена внутренним трением в результате движения тела в вязкой среде (рис.4.4).

Ограничившись, случаем малых колебаний, воспользовавшись основным законом динамики, можно записать уравнение затухающих колебаний.

На систему в этом случае действуют две силы: возвращающая F₁ и сила сопротивления F₂, которая при малых скоростях движения v пропорциональна скорости:

F₁ = - kx; (4.25)

F₂ = - rv = - rdx/dt, (4.26)

где r - коэффициент сопротивления.

Таким образом, уравнение затухающих колебаний будет иметь вид

ma = F₁ + F₂; ma = F₁ + F₂.;

или окончательно

. (4.27)

Этому дифференциальному уравнению (второго порядка) затухающих колебаний соответствует решение

, (4.28)

где А = x₀e^-βt - амплитуда колебаний, которая убывает по экспоненциальному закону;

β = r/(2m) или - коэффициент затухания, характеризующий быстроту убывания амплитуды с течением времени.;

 - время, в течение которого амплитуда колебаний убывает в два раза;

ω₀² = k/m – собственная частота колебаний системы, т.е. та частота, совершались бы свободные колебания системы в отсутствии сопротивления среды (r = 0).

Решая дифференциальное уравнение, можно определить частоту и период затухающих колебаний:

; . (4.29)

Отметим, что на практике , поэтому можно считать .

Так как

Рис.4.5

, (4.30)

то действительно при t, A0.

Графически затухающие колебания можно представить так, как показано на рис.4.5.

Основными характеристиками затухающих колебаний являются декремент и логарифмический декремент затухания.

Декремент затухания - отношение двух смещений, отличающихся друг от друга по времени на период

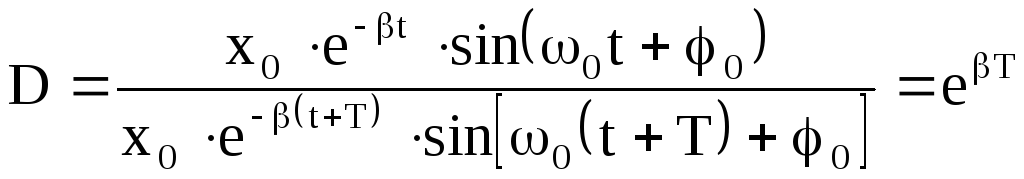. (4.31)

Декремент затухания характеризует быстроту затухания в зависимости от числа колебаний. По его величине можно определить число колебаний, через которое амплитуда уменьшится в определенное число раз.

Логарифмический декремент затухания - величина, равная натуральному логарифму от декремента затухания

 = lnD = ln(e^βΤ) = βT. (4.32)

Зная логарифмический декремент затухания  и период колебаний Т, можно записать закон убывания амплитуды в виде

А = А₀e^-(/T)t. (4.33)

Таким образом, логарифмический декремент затухания характеризует затухание колебаний за период. По величине он обратен числу колебаний, совершаемых за то время, за которое амплитуда колебаний уменьшится в "e" раз (=1/N_e). Если за время t амплитуда уменьшится в "e" раз, то система за это время совершит N_e = t/T колебаний.

Силы трения и сопротивления влияют на частоту колебаний. При достаточно большом трении замедление колебаний может оказаться настолько значительным, что колебания прекратятся, практически едва начавшись. Такие колебательные движения называются апериодическими. В этом случае:

1) при βω₀ частота колебаний 0 - убывает, а период колебаний , т.е. возрастает;

2) при βω₀ характер процесса зависит от начальных условий (x₀ и v₀ = dx₀/dt):

а) - это условие будет выполнено, если выведенной из положения равновесия системе сообщить достаточно сильный толчок к положению равновесия;

б) v₀ = 0 – выполняется, если системе сообщается толчок недостаточной силы.

Для характеристики колебательной системы пользуются понятием добротности Q, которую при малых значениях логарифмического декремента затухания можно определить по формуле

Q = π/λ = πN_e = π/(βT₀) = ω₀/(2β). (4.34)

Добротность пропорциональна числу колебаний N_e, совершаемых за время t (время релаксации), за которое амплитуда уменьшится в "e" раз.

Для механической колебательной системы с массой m, коэффициентом жесткости k и коэффициентом трения r, добротность определяется соотношением

. (4.35)