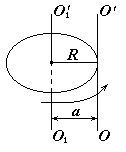
3.3.3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета (сила Кориолиса)

При движении тела относительно вращающейся системы отсчета, кроме центробежной силы инерции, появляется еще одна сила, называемая силой Кориолиса или кориолисовой силой инерции. Рассмотрим проявление этой силы на одном частном примере.

Рис.3.5

Относительно вращающейся системы отсчета тело движется по окружности, лежащей в плоскости, перпендикулярной к оси вращения, причем центр окружности лежит на этой оси. Такой случай реализуется, например, когда тело движется вдоль параллели (экватора) по поверхности вращающегося земного шара (рис.3.5).

Относительно неподвижной (инерциальной) системы тело движется равномерно по окружности радиуса R. Так что ускорение тела в этой системе (центростремительное) может быть представлено в виде

, (3.31)

где .

После выполнения простых преобразований получим

или . (3.32)

По отношению к вращающейся системе тело обладает центростремительным ускорением

. (3.33)

Откуда следует, что первое слагаемое в (3.32) представляет собой ускорение . Следовательно,

. (3.34)

В соответствии с этим выражением сила инерции оказывается состоящей из двух компонент:

. (3.35)

Первая из них есть центробежная сила инерции , вторая – кориолисова сила. Силаимеет направление:

а) от центра, если скорости v^’ и R совпадают по направлению;

б) к центру, если скорости v и R направлены в противоположные стороны.

В общем случае, когда вектор скорости v материальной точки, перемещающейся по вращающейся поверхности, направлен произвольно, математическое выражение силы Кориолиса таково:

. (3.36)

Вектор F_к перпендикулярен векторам скорости v^’ тела и угловой скорости вращения ω системы отсчета в соответствии с правилом правого винта.

В таблице 3.1 наглядно показаны силы инерции, возникающие в зависимости от состояния частицы в неинерциальной системе отсчета и характера движения этой системы относительно инерциальной системы отсчета.

Таблица 3.1

Силы инерции, возникающие в неинерциальной системе отсчета в зависимости от состояния частицы

Состояние частицы в неинерциальной системе	Название и математическое выражение силы инерции	Характер движения относительно ИСО
Частица находится в покое	Сила инерции	Система движется прямолинейно с ускорением
	Центробежная сила инерции	Система вращается с угловой скоростью
Частица движется со скоростью	Кориолисова сила инерции

Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчета, например, относительно Земли. Поэтому действием этих сил объясняется ряд наблюдаемых на Земле явлений (подмывание берегов рек; неравномерное изнашивание железнодорожных рельсов; отклонение падающих на поверхность Земли тел; поведение маятника Фуко, явившееся в свое время одним из доказательств вращения Земли). Применительно к рассмотренному выше случаю движения можно привести такой пример: при стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к Земле, если выстрел произведен в направлении на запад (т.е. в направлении, противоположном вращению Земли), и поднимать кверху, если выстрел произведен в восточном направлении.

Таким образом, основной закон динамики для неинерциальных систем отсчета можно записать в виде

ma^’ = F + F_ин + F_ц +F_к, (3.37)

где F, F_ин, F_ц, F_к - ранее рассмотренные силы, действующие в неинерциальных системах отсчета.

Надо еще раз отметить, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета. Поэтому они не подчиняются третьему закону Ньютона, так как если на какое-либо тело действует сила инерции, то не существует противодействующей силы, приложенной к данному телу. Два основных положения динамики, согласно которым ускорение всегда вызывается силой, а сила всегда обусловлена взаимодействием между телами, в системах отсчета, движущихся с ускорением, одновременно не выполняются.

Для любого из тел, находящегося в неинерциальной системе отсчета, силы инерции являются внешними, следовательно, здесь нет замкнутых систем. Это означает, что в неинерциальных системах отсчета не выполняются законы сохранения импульса, момента импульса, энергии.

Силы инерции действуют только в неинерциальных системах отсчета. В инерциальных системах отсчета таких сил нет.

Силы инерции пропорциональны массам частиц (тел, систем) и при прочих равных условиях сообщают этим телам одинаковые ускорения. Поэтому в "поле сил инерции" эти тела движутся совершенно одинаково, если только одинаковы начальные условия. Тем же свойством обладают тела, находящиеся под действием сил поля тяготения.

При некоторых условиях силы инерции и силы тяготения невозможно различить. Например, движение тел в равноускоренном лифте происходит точно так же, как и в неподвижном, висящем в однородном поле тяготения. Никакой эксперимент, выполненный внутри лифта, не может отделить однородное поле тяготения от однородного поля сил инерции.

Аналогия между силами тяготения и силами инерции лежит в основе принципа эквивалентности гравитационных сил и сил инерции (принципа эквивалентности Эйнштейна): «Все физические явления в поле тяготения происходят совершенно так же, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы». Этот принцип является основой общей теории относительности.

3.4. Элементы динамики материальной точки и твердого тела, совершающих вращательное движение относительно неподвижной оси вращения. Основные понятия и определения: момент силы, момент импульса, момент инерции. Теорема Штейнера. Основное уравнение динамики вращательного движения

Основной задачей динамики вращательного движения является задача нахождения угловых ускорений, сообщаемых известными силами. Однако одна и та же сила, в зависимости от расстояния между ее направлением и осью вращения, сообщает различные угловые ускорения. Для описания вращательного движения введены специфические параметры: момент силы, момент инерции тела, момент импульса. Благодаря этим параметрам достигается подобие основных уравнений динамики поступательного и вращательного движения.

Момент силы характеризует вращательный эффект силы при действии ее на твердое тело. Различают момент силы относительно центра (точки) и оси вращения.

Моментом силы относительно центра вращения называют векторную физическую величину, модуль которой равен произведению модуля силы на плечо:

M = Fl или M = Fl, (3.38)

где l - плечо силы - кратчайшее расстояние от направления действия силы до центра вращения.

Вектор M направлен вдоль перпендикуляра к плоскости, на которой находится центр вращения и сила. Направление его определяется правилом правого винта. Так как

l = rsinα,

где r численное значение радиус-вектора r, который направлен из центра вращения в точку приложения силы;

α - угол между направлениями F и r,

то

M = Frsinα (3.39)

или в векторной форме

M = [rF]. (3.40)

Момент нескольких сил, имеющих одну точку приложения, равен алгебраической сумме моментов слагаемых сил:

. (3.41)

Этот момент называют главным или результирующим моментом системы сил относительно неподвижной точки вращения (центра; полюса).

Из третьего закона Ньютона следует, что моменты внутренних сил взаимодействия материальных точек системы относительно центра вращения попарно компенсируются. Следовательно, при вычислении главного момента сил необходимо учитывать только внешние силы, действующие на рассматриваемую механическую систему. Иначе результирующий момент внутренних сил системы равен нулю.

Р

Рис.3.6

ассмотрим вращение тела вокруг закрепленной оси (рис.3.6). Тело является абсолютно жестким. Пусть к двум точкам этого тела приложены силы,.,– радиус-вектора, проведенные из центра вращения в точку приложения силы. Предполагается, что вектора сил лежат в плоскости, перпендикулярной оси вращения. Во всяком случае, понятно, что компонента силы, параллельная оси вращения, при закрепленной оси никакого вращательного действия произвести не может.

Разложим силу на плоскости на две составляющие – касательную и нормальную к окружности, по которой движется точка приложения силы:

. (3.42)

Вращательное действие силы определяется только касательной составляющей силы и положением точки приложения силы по отношению к центру вращения, т.е. радиусом . Введем угол , образованный между направлениями векторови. Тогда получим

(3.43)

Вращательное действие любой силы будет пропорционально произведению:

или . (3.44)

Выражение представляет собой плечо силы, т.е. кратчайшее расстояние от линии действия силы до оси вращения.

По правилу "рычага" равновесие наступает при равенстве

. (3.45)

Произведение носит название момента силы относительно оси вращения. Момент силы – это вектор, определяемый как векторное произведение:

. (3.46)

Модуль выражается следующим образом:

. (3.47)

Этот вектор всегда перпендикулярен плоскости, образованной векторами и, т.е. направлен по оси вращения "по правилу правого винта". Поэтому в случае закрепленной оси вращения вместо векторного представления момента силы можно воспользоваться алгебраическим представлением. Если сила вращает тело по часовой стрелке, то момент силы будем считать положительным, если сила вращает тело против часовой стрелки, то моменту этой силы будем приписывать знак "минус". Заметим, что на рис.3.6 направление оси выбрано "от нас, за чертеж". Для силимоменты равныи. Условие равновесия может быть записано как

. (3.48)

Силы ине вызывают вращение, если их моментыиравны по величине и противоположны по направлению.

В общем случае, когда на тело действует сил, рассматривают полный момент сил:

. (3.49)

И условие равновесия тела с закрепленной осью вращения сводится к виду:

. (3.50)

Оказывается, что один и тот же момент внешней силы, действующей на различные тела (материальные точки), сообщает им различные угловые ускорения.

Для характеристики инертности тел (материальных точек) вращательному движению вводится в рассмотрение физическая величина, называемая моментом инерции материальной точки или тела (I относительно неподвижной оси (центра вращения). Чем больше , тем меньше угловое ускорение получит тело под действием данного момента силы .

Моментом инерции материальной точки относительно какой-либо оси или центра вращения называется физическая величина, равная произведению массы материальной точки на квадрат расстояния от нее до оси или центра вращения:

I = mr². (3.51)

Момент инерции тела - величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.

Для тела с закрепленной осью вращения момент инерции представляет собой положительную скалярную величину.

Прямой способ вычисления момента инерции тела состоит в следующем: мысленно тело разбивают на совокупность материальных точек, записывают момент инерции -й материальной точки, полный момент инерции получают суммированием элементарных моментов:

Рис.3.7

или (3.52)

Рассмотрим несколько примеров:

Рис.3.8

1. Момент инерции обруча, вращающегося вокруг собственной оси (рис.3.7). Обруч считаем "тонким" и однородным по плотности. В данном случае все материальные точки (элементарные массы) расположены на одинаковом расстоянии от оси вращения. Поэтому

. (3.53)

2. Момент инерции стержня относительно оси, проходящей перпендикулярно к нему через его середину (рис.3.8). Стержень считаем "тонким", однородным по сечению и распределению плотности. Длина стержня – . Момент инерции материальной точки представим в виде дифференциала

(3.54)

где – площадь сечения.

Рис.3.9

. (3.55)

3. Момент инерции сплошного цилиндра относительно собственной оси (рис.3.9). Цилиндр (диск) считаем однородным по плотности. Радиус цилиндра – , длина –. В данном случае целесообразно разбить цилиндр на совокупность тонкостенных цилиндров, соосных друг с другом. Элементарный момент инерции представим в виде дифференциала

. (3.56)

Момент инерции цилиндра получим путем интегрирования:

. (3.57)

4. Момент инерции шара относительно оси, проходящей через его центр, можно определить аналогично и вычисляется по формуле

. (3.58)

Рис.3.10

Таким образом, момент инерции тела существенно зависит от его геометрии (формы), а также от положения оси вращения, т.е. зависит от распределения массы тела относительно оси вращения. Если выбрать новую ось вращения, оставив без изменения форму и размеры тела, то изменится и момент инерции тела. Поэтому определенный смысл момент инерции имеет только в том случае, когда задана ось вращения. Значительное упрощение в вычислениях момента инерции тела относительно оси, не проходящей через центр масс этого тела, можно получить, применяя теорему Штейнера, формулировку которой мы примем без доказательства (рис.3.10): «Момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела относительно оси, параллельной данной и проходящей через центр масс тела, I₀ и произведения массы тела m₀ на квадрат расстояния между осями», т.е.

. (3.59)

Рис.3.11

Примеры применения теоремы Штейнера:

1. Момент инерции диска относительно оси , параллельной геометрической оси диска и проходящей через его край (рис.3.11).

Здесь , . Поэтому

. (3.60)

Рис.3.12

2. Момент инерции шара относительно оси, касательной к его поверхности (рис.3.12).

Здесь , . Тогда

. (3.61)