3.2. Динамика твердого тела, вращающегося вокруг своей оси

Для описания вращательного движения твердого тела необходимо ввести три новые физические величины: момент силы, момент импульса и момент инерции. Эти величины входят в основные уравнения динамики вращательного движения, которое будет получено в 3.2.2.

3.2.1. Динамические характеристики вращающегося твердого тела

Основными динамическими характеристиками вращающегося твердого тела являются момент силы, момент импульса и момент инерции.

Для характеристики внешнего механического действия на тело, вызывающего изменение его вращения, вводят понятие момента силы. Различают момент силы относительно неподвижной точки и относительно неподвижной оси.

Моментом силы относительно точки вращения О называется векторная величина, характеризующая вращающее действие силы, приложенной к телу, и равная векторному произведению

, (3.18)

Рис. 3.4

где - радиус-вектор, проведенный из точкиO в точку приложения силы (точка А на рис. 3.4).

Вектор направлен перпендикулярно плоскости, проходящей через радиус-вектори силу, в сторону, откуда поворот, вызываемый силой, виден против хода часовой стрелки.

Модуль момента силы (формула (2.51)) равен:

, (3.19)

где - угол между векторамии,-длина перпендикуляра опущенного из точкиO на направление действия силы. Величина называется плечом действия силы относительно точкиO. Из формулы (3.19) следует, что при переносе точки приложения силы вдоль направления ее действия момент этой силы относительно одной и той же неподвижной точкиO не изменяется. Если направление действия силы проходит через точку О, то момент силы относительно этой точки равен нулю.

Единица момента силы – ньютон, умноженный на метр (Н·м).

Введем понятие момента силы относительно неподвижной оси.

Моментом силы относительно неподвижной оси называется скалярная величина, равная проекции на эту ось вектора момента силы относительно произвольной точки оси, то есть, как следует из рис. (3.4),

, (3.20)

где - момент силы относительно осиZ, М - модуль вектора момента силы относительно точки O на оси Z, - угол между вектороми направлением осиZ.

Величина не зависит от выбора положения точкиО на оси Z.

Иногда моментом силы относительно неподвижной оси называют составляющую вдоль оси Z вектора момента силы относительно точки O,

, (3.21)

где - орт оси Z.

Рис. 3.5

Моментом импульса материальной точки относительно центра О (точки) вращения называется векторная величина, являющаяся мерой механического движения и равная векторному произведению

, (3.22)

где - момент импульса относительно центра вращения,- радиус-вектор движущейся точки, проведенный из центра вращения (точкаO на рис. 3.5); - импульс, масса и скорость материальной точки.

Направлен вектор перпендикулярно плоскости, проходящей через векторыив сторону, откуда движение материальной точки вокруг точкиO (см. рис. 3.5) видно против хода часовой стрелки.

Единица момента импульса - килограмм-метр в квадрате, деленный на секунду (кг_*м²/с).

Моментом импульса системы материальных точек (тела) относительно точки вращения называется вектор, равный векторной сумме моментов импульса относительно того же центра всех материальных точек системы, то есть

, (3.23)

где - момент импульса системы материальных точек,- момент импульса-ой материальной точки.

Моментом импульса системы материальных точек (тела) относительно неподвижной оси называется скалярная величина, равная проекции на эту ось вектора момента импульса этой системы относительно произвольной точки оси, то есть, как следует из рис. 3.5,

, (3.24)

где - модуль момента импульса относительно осиZ, - модуль вектора момента импульса относительно точки О на оси Z, - угол между вектором и направлением осиZ.

Выбор положения точки О на оси Z не влияет на значение .

Иногда моментом импульса тела относительно неподвижной оси называют составляющую вдоль оси Z вектора момента импульса тела относительно точки О

, (3.25)

где - орт оси Z.

Найдем выражение для момента импульса тела, вращающегося вокруг неподвижной оси Z, с угловой скоростью (рис. 3.6).

Рис. 3.6

На основании выражений (3.22) и (3.24) и (2.50) запишем для -ой материальной точки тела:

(3.26)

Просуммируем выражение (3.26) по всем n материальным точкам, тогда получим для тела в целом

. (3.27)

Моментом инерции тела относительно неподвижной оси называется положительная скалярная величина, равная сумме произведений масс всех материальных точек на квадраты их кратчайших расстояний до оси вращения, то есть:

, (3.28)

где - масса материальной точки и ее кратчайшее расстояние до оси вращения.

Единица момента инерции - килограмм-метр в квадрате (кг_*м²).

С учетом (3.28) выражение (3.27) примет вид

^. (3.29)

С учетом направлений векторов и(рис. 3.6) и формулы (3.25) формулу (3.29) можно записать и в векторной форме

. (3.30)

Из (3.30) следует, что составляющая вектора момента импульса тела вдоль неподвижной оси равна произведению момента инерции тела относительно той же оси на угловую скорость вращения.

Направления векторов и, как следует из (3.30), совпадают.

Момент инерции тела является его мерой инертности при вращательном движении вокруг неподвижной оси, подобно тому, как масса тела является мерой его инертности в поступательном движения.

Ось вращения твердого тела сохраняет неизменное положение в пространстве, если она механически закреплена, например, с помощью подшипников. У тела произвольной формы и у симметричного тела, если ось вращения не совпадает с осью симметрии, подшипники действуют на ось с определенными силами. Однако, как доказано в теоретической механике, для любого тела существуют оси вращения, которые сохраняют свою ориентацию в отсутствие внешних сил. Такие оси называются свободными. У тела любой формы и с произвольным распределением масс существует три взаимно перпендикулярные оси, проходящие через его центр масс, которые являются свободными. Эти оси называются главными осями инерции тела.

В качестве примера, укажем главные оси инерции некоторых однородных симметричных тел. Для однородного параллелепипеда свободными главными осями являются три оси, проходящие через центры противоположных граней. У однородного цилиндра и тел, обладающих цилиндрической симметрией, одна из главных осей совпадает с осью цилиндра, а две другие взаимно перпендикулярные оси проходят через центр масс перпендикулярно первой оси. У однородного шара главными осями являются любые три взаимно перпендикулярные оси, проходящие через его центр.

Моменты инерции тел относительно главных осей называются главными моментами инерции.

Ф

Рис. 3.7

ормула (3.28) определяет момент инерции тела относительно неподвижной оси в случае, когда тело заменено системой материаль-ных точек. Для расчета моментов инерции тел удобнее их рассматривать как сплошные среды с непрерывным рас-пределением массы. Для сплошного тела роль материальной точ-ки выполняет бесконеч-но малый элемент массы , где- плотность вещества в теле,- физически бесконечно малый эле-мент объема, который содержит такое минимальное количество молекул, что свойства вещества в его пределах можно считать одинаковыми (и при этом еще не п

Рис. 3.8

роявляется дискретность вещества).

Расчет момента инерции сплошного тела можно провести, если в формуле (3.28) суммирование по дискретным точкам заменить (см. формулы 2.17 и 2.18) интегрированием по объему тела, то есть

^. (3.31)

Из формул (3.28) и (3.31) следует, что момент инерции тела зависит от его формы, размеров, распределения массы и от расположения оси, относительно которой он вычисляется.

В качестве примера рассчитаем по формуле (3.31) момент инерции стержня, относительно главной оси инерции, проходящей перпендикулярно оси симметрии через центр масс (рис. 3.7).

Выберем на расстоянии от осиz бесконечно малый элемент стержня длиной . Масса этого элемента может быть выражена через плотность и объем

, (3.32)

где - площадь поперечного сечения стержня. Подставим (3.32) в (3.31) и учтем, что и интегрирование по объему в данном случае сводится к интегрированию по длине стержня:

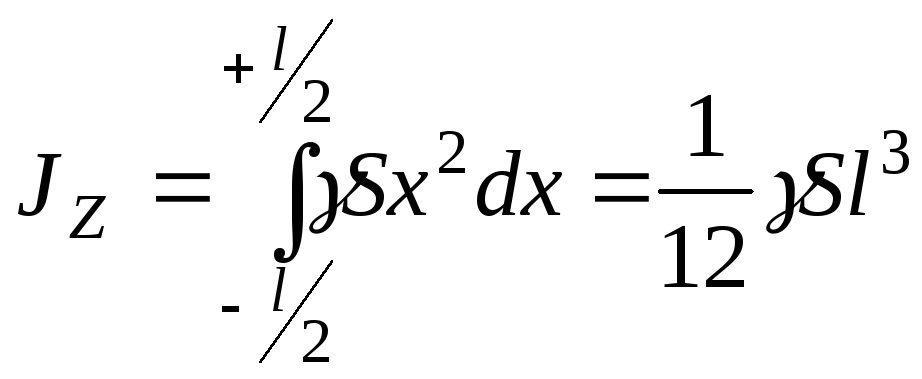или учитывая, что

масса стержня равна , получим

^. (3.33)

Неподвижная ось вращения может проходить и не через центр масс. Для вычисления моментов инерции относительно любой оси применяют теорему Гюйгенса-Штейнера, которая приводится без доказательства:

Момент инерции тела относительно какой-либо оси равен его моменту инерции относительно параллельной оси, проходящей через центр масс, сложенному с произведением массы тела на квадрат расстояния между осями.

Формулировка теоремы поясняется рис. 3.8 и следующей формулой:

. (3.34)

С помощью формулы (3.31) и теоремы Гюйгенса-Штейнера (3.34) могут быть вычислены моменты инерции некоторых тел простейшей формы (Таблица I).

Таблица I

Тело	Положение оси	Момент инерции
Полый тонкостенный цилиндр радиуса R, массой m	Ось симметрии
Сплошной цилиндр (или диск) радиуса R, массой m	Ось симметрии
Прямой тонкий стержень длиной l и массой m	Ось Z перпендикулярна к стержню и проходит через его середину Ось Z перпендикулярна к стержню и проходит через его конец
Шар радиуса R и массой m	Ось Z проходит через центр шара Ось Z проходит на расстоянии a от центра шара