3.2.2. Основной закон динамики твердого тела, вращающегося вокруг неподвижной оси

Выше было отмечено, что твердое тело можно мысленно представить в виде системы материальных точек. Рассмотрим тело, состоящее из n материальных точек. Будем считать, что тело (рис. 3.9) может вращаться только вокруг оси Z. Пусть - масса -ой точки системы, а - радиус-вектор, проведенный в эту точку из начала координат инерциальной системы отсчета (точкаО). Обозначим через силу, действующую на -ую точку со стороны -ой материальной точки системы, а через- равнодействующую всех внешних сил, приложенных к -ой точке.

По второму закону Ньютона уравнение движения этой материальной точки имеет вид

^. (3.35)

Умножим обе части этого уравнения слева векторно на :

Рис. 3.9

(3.36)

Знак производной в левой части (3.35) можно вынести за знак векторного произведения, так как

,

поскольку , как векторное произведение двух одинаково направленных векторов.

Следовательно, уравнение (3.36) можно переписать в виде

^. (3.37)

Перепишем уравнение (3.37) с учетом введенных выше динамических характеристик (3.18) и (3.22)

(3.38)

и просуммируем по всем n материальным точкам системы:

^. (3.39)

Векторная сумма моментов всех внешних сил, приложенных ко всем материальным точкам системы, называется результирующим моментомвнешних сил относительно точкиO:

. (3.40)

Векторная сумма моментов относительно точкиО всех внутренних сил взаимодействия между материальными точками системы равна нулю:

^. (3.41)

Это объясняется тем, что по третьему закону Ньютона силы иравны по модулю, имеют общее направление действия, но направлены в противоположные стороны. Поэтому моменты этих сил взаимно компенсируют друг друга, то есть

. (3.42)

На основании соотношений (3.23), (3.40) и (3.41) можем переписать уравнение (3.39):

. (3.43)

Уравнение (3.43) может быть записано и для составляющих векторов ина ось вращенияZ

. (3.44)

Это уравнение называется основным законом динамики твердого тела, вращающегося вокруг неподвижной оси (закон изменения момента импульса относительно неподвижной оси):

скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой оси всех действующих на него внешних сил.

С учетом выражения (3.30) уравнение (3.44) можно представить в виде

(3.45)

или

, (3.46)

откуда с учетом (2.45) можем записать

(3.47)

Из уравнения (3.47) следует, что угловое ускорение твердого тела, вращающегося вокруг неподвижной оси, прямо пропорционально результирующему моменту относительно этой оси всех внешних сил, действующих на тело, и обратно пропорционально моменту инерции тела относительно этой же оси.

Кроме того, из уравнения (3.47) следует, что угловое ускорение совпадает по направлению с результирующим моментом всех внешних сил.

3.2.3. Гироскоп. Понятие о гироскопическом эффекте

Гироскопом называется осесимметричное тело, быстро вращающееся вокруг оси симметрии, которая может изменять свое положение в пространстве.

Р

Рис. 3.10

ассмотрим такое тело, свободно подвешенное в пространстве и вращающееся с угловой скоростью вокруг оси ох (рис.3.10). Приложим к оси гироскопа пару сил , стремящихся повернуть его вокруг осиоy. Опыт показывает, что в этом случае наблюдается интересный эффект - ось гироскопа поворачивается не вокруг оси оy, а вокруг оси оz. Описанный эффект получил название гироскопического и состоит в том, что ось гироскопа поворачивается в сторону момента внешних сил , а не в направлении действия сил (рис 3.10). Движение оси гироскопа называется прецессией. Покажем, что гироскопический эффект объясняется основным законом динамики вращательного движения. При быстром вращении гироскопа угловая скорость прецессии оказывается значительно меньше угловой скорости гироскопа. Поэтому можно считать, что вектор результирующей угловой скорости направлен практически по оси ох и равен по модулю . Ось симметрии гироскопа является его главной осью инерции и, следовательно, момент импульса гироскопа также направлен вдоль этой оси и равен , где- главный момент инерции гироскопа.

Приращение вектора угловой скорости под действием момента пары силза бесконечно малое времяможно выразить из основного уравнения динамики вращающегося тела (3.46):

^. (3.48)

Вектор момента силнаправлен по оси оy. Из (3.48) следует, что вектор должен быть направлен также параллельно осиоy (рис.3.10). Таким образом, вектор , а вместе с ним и ось гироскопа, под действием пары силдолжны вращаться вокруг оси оz.

Угловую скорость этого вращения можно определить, если учесть, что угол, на который повернется за времявектор, может быть выражен черези(как центральный угол, опирающийся на дугуокружности радиусом(рис.3.10)):

^. (3.49)

Подставим в (3.49) выражение для модуля вектора из (3.48), тогда получим

^. (3.50)

Из выражения (3.50) находим угловую скорость прецессии:

(3.51)

Отметим, что движение оси гироскопа (прецессия) не обладает инерцией - оно прекращается сразу же как только прекращается действие момента сил.

Р

Рис. 3.11

ассмотрим прецессию гироскопа, ось которого опирается на горизонтальную поверхность в некоторой точке О, остающейся все время неподвижной (рис. 3.11). Такой гироскоп называетсяволчком. Пусть ось волчка составляет с вертикалью угол . Тогда сила тяжести создает относительно точки О момент, модуль которого равен

Рис. 3.1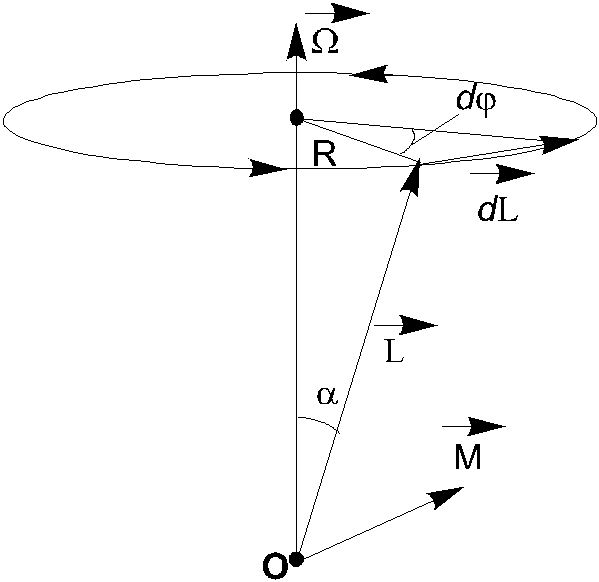2

, (3.52)

где - расстояние от центра тяжести волчка до точки опоры О.

Этот момент стремиться повернуть ось волчка в положение более близкое к горизонтальному. Однако волчок ведет себя иначе - его ось начинает перемещаться в пространстве так, что угол остается постоянным, то есть ось гироскопа движется с постоянной угловой скоростью по поверхности конуса с вершиной в точке О (рис. 3.11). Определим угловую скорость прецессии волчка. На рис. 3.12 показано взаимное расположение вектора момента импульса волчка, совпадающее по направлению с его осью, вектора- момента силы тяжести и вектора угловой скорости прецессии оси волчка. В результате прецессии векторописывает конус с основанием, радиус которого равен. Из основного уравнения динамики вращательного движения (3.43) найдем приращение вектораза время:

. (3.53)

Модуль приращения вектора , как следует из рис. 3.12, можно представить в виде

. (3.54)

Из (3.53) найдем соотношение между модулями векторов ии учтем (3.54), тогда получим

,

откуда находим угловую скорость прецессии оси волчка:

^. (3.55)

Подставляя в формулу (3.55) выражение (3.52) и (3.30), окончательно получим

^. (3.56)

Из формулы (3.56) следует, что угловая скорость прецессии оси волчка не зависит от угла между его осью и вертикалью.

Заметим, что приведенное описание движения оси гироскопа и волчка справедливо в том случае, когда угловая скорость прецессии значительно меньше угловой скорости вращения самого волчка.