2.2.3. Связь между линейными и угловыми величинами

Р

Рис. 2.13

ассмотрим одну из точек тела, вращающегося вокруг осиОО', например точку М на рис.2.13. За малое время t точка М пройдет по окружности путь S, а ее радиус-вектор повернется на угол.

Используем известное из геометрии соотношение S=. Разделим это равенство на t и возьмем предел слева и справа при t0, тогда получим

^. (2.48)

Запишем равенство (2.48) с помощью понятия производной (стр.21)

^. (2.49)

С учетом формул (2.9) и (2.41) выражение (2.49) переходит в следующее:

. (2.50)

Выражение (2.50) устанавливает связь между модулями трех векторов - вектора скорости (для вращательного движения скорость называется линейной),- радиус-вектора точки относительно центра окружности О' и - вектора угловой скорости.

Для установления соотношения между векторами ,инеобходимо применить так называемоевекторное произведение векторов. Познакомимся с этим понятием.

Векторным произведением двух векторов иназывается вектор, обладающий следующими свойствами:

1. модуль вектора равен произведению модулей перемножаемых векторов на синус угла между ними (рис 2.14):

; (2.51)

2. вектор перпендикулярен к плоскости в которой лежат векторыи, а его направление определяется по правилу правого винта: вращение винта по кратчайшему пути от векторак векторувызывает его поступательное движение в направлении вектора(рис. 2.14).

Символически векторное произведение записывается в виде:

. (2.52)

Как следует из рис. 2.13 , поэтому с учетом соотношений (2.50), (2.51) и (2.52) линейную скорость



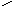
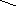
Рис. 2.14

любой точки вращающегося тела можно представить в виде

. (2.53)

При неравномерном вращении угловая, и, следовательно, линейная скорости будут функциями времени (формула 2.50). Продифференцируем по времени формулу (2.50) и учтем, что направлена по касательной к окружности (рис 2.13):

^,

откуда с учетом выражений (2.36) и (2.45) получаем

. (2.54)

Соотношение между векторами и можно записать с помощью векторного произведения (рис. 2.13, 2.14,

формулы 2.51, 2.52):

. (2.55)

Скорость каждой точки вращающегося тела изменяет свое направление, поэтому кроме тангенциального ускорения у нее имеется и нормальное ускорение (формула 2.35), модуль которого в рассматриваемом случае равен

(2.56)

Перепишем формулу (2.56) с учетом соотношения (2.50) в виде

. (2.57)

С учетом направлений векторов ,исоотношение (2.57) может быть записано с помощью векторного произведения в виде

. (2.58)

Вектор полного ускорения определяется через свои компоненты по формулам (2.37) и (2.38):

, ^. (2.59)

§3. Динамика

3.1. Динамика материальной точки и твердого тела, движущегося поступательно

В основе динамики лежат три закона Ньютона, сформулированные им в 1687 году в сочинении "Математические начала натуральной философии". Эти законы явились результатом обобщения большого числа наблюдений и опытных фактов, связанных с движением макроскопических тел со скоростями много меньшими скорости света в вакууме. Рассмотрим смысл и содержание этих законов.