Модуль ускорения определяется выражением

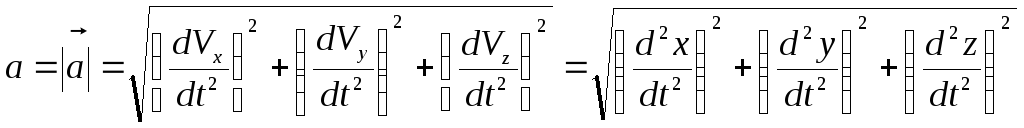. (2.21)

Выше было отмечено, что вектор ускорения материальной точки характеризует изменение скорости по модулю и направлению. Оказывается, что векторможно разложить на две составляющие, одна из которых характеризует изменение только модуля скорости, а другая - только его направления. Такое разложение возможно при любом виде движения материальной точки. В качестве примера покажем это для случая плоского движения точки по произвольной криволинейной траектории.

Пусть материальная точка M совершает неравномерное плоское движение по криволинейной траектории (рис. 2.6). Проведем в точке М два взаимно перпендикулярных единичных вектора (орта) илежащих в плоскости траектории. Векторнаправлен по касательной к траектории в сторону движения материальной точки, то есть в направлении ее скорости. Вектор, проведен в сторону вогнутости траектории по линии, соединяющей точку M с центром О кривизны траектории для данной ее точки.

В этих условиях ускорение может быть разложено на две следующие составляющие:

. (2.22)

В

Рис. 2.7

качестве примера рассмотрим неравномерное движение точки М по окружности (рис 2.7). В момент времени t точка М находится в положении 1 и имеет скорость. Через малый промежуток времениt точка переместится в положение 2 и будет иметь скорость . Найдем приращение вектора скоростиза времяt. Для этого перенесем вектор без изменения его направления так, чтобы его начало совпало с началом вектора(рис. 2.8). Векторизображен направленным отрезком, проведенным из конца векторав конец вектора. Разложим векторна две составляющие_n и _. Составляющую _n выберем так, чтобы расстояние от точки 1 до конца вектора было равно. При таком выборе_n, составляющая _ будет иметь модуль равный приращению модуля (величины) скорости за время t, то есть

|_|=||. (2.27)

Введем единичный вектор , совпадающий по направлению с вектором_, тогда его можно будет представить в виде

_=. (2.28)

Вектор _n также можно представить в виде произведения его модуля на единичный вектор , задающий его направление

_n =|_n |.(2.29)

Угол между векторами и () равен, то есть углу между векторами и () (рис 2.7 и 2.8). При малыхt модуль вектора _n можно приближенно заменить дугой окружности радиуса || (рис. 2.8):

_n. (2.30)

Угол  можно выразить через радиус окружности и пройденный точкой М путь S за время t (рис. 2.7) с помощью известного из геометрии соотношения

=^. (2.31)

С учетом (2.31) формула (2.30) принимает вид:

_n . (2.32)

Найдем ускорение точки М в положении 1 (рис. 2.7). Для этого учтем, что =_n +_, и воспользуемся формулой (2.21)

(2.33)

Рис 2.8

С учетом выражения (2.32) первый предел справа принимает вид:

^. (2.34)

В точке 1 траектории V и имеют фиксированные значения, а. Кроме того, приt0 вектор переходит в вектор- вектор главной нормали к траектории в точке 1 (рис. 2.8). Таким образом, вычисляя предел в (2.34) и обозначая его через, получим

^. (2.35)

Второй предел в выражении (2.33) обозначим через и учтем выражение (2.28), тогда можем записать:

^. (2.36)

При вычислении предела в (2.36) учтено, что при t0 вектор переходит в вектор- единичный вектор касательной к траектории в точке 1 (рис. 2.8).

Таким образом, вектор ускорения точки в любой момент времени может быть представлен в виде суммы двух векторов:

. (2.37)

Вектор - называется нормальным ускорением и характеризует изменение скорости по направлению.

Вектор - называется тангенциальным (касательным) ускорением и характеризует изменение скорости по величине.

Модуль полного ускорения в соответствии с выражениями (2.35), (2.36) и (2.37) равен:

^. (2.38)

Если траектория не окружность, а произвольная кривая, то в формуле (2.38) представляет собой радиус кривизны траектории в точке, для которой определяется полное ускорение.