
- •Глава III. Магнетизм
- •§12. Магнитное поле в вакууме
- •12.1. Опыт Эрстеда. Индукция магнитного поля
- •Магнитное поле
- •12.2. Поток вектора . Теорема Гаусса
- •12.3 Магнитное взаимодействие токов. Закон Ампера
- •Закон Био-Савара-Лапласа
- •12.5 Принцип суперпозиции. Применение закона
- •12.5.1 Магнитное поле кругового тока
- •12.5.2. Магнитное поле прямого тока
- •12.6. Теорема о циркуляции вектора магнитной индукции. Вихревой характер магнитного поля
- •12.7. Магнитное поле соленоида
- •12.7. 1. Магнитное поле тороида
- •§13. Магнитное поле в веществе
- •Электрона и атома
- •13.2. Намагничивание вещества. Вектор намагниченности
- •Поле в магнетиках. Напряженность магнитного поля
- •13.4. Магнитная восприимчивость и магнитная проницаемость
- •13.5. Теорема о циркуляции вектора
- •13.6. Расчет магнитного поля длинного стержневого проводника с током
- •Граничные условия для векторов и
- •13.8. Расчет магнитного поля в неоднородных средах
- •Типы магнетиков
- •13.9.1. Природа диамагнетизма
- •13.9.2. Природа парамагнетизма.
- •13.9.3. Ферромагнетизм
- •13.9.4. Природа ферромагнетизма
- •§ 14. Заряды и токи в магнитном поле
- •14.1. Сила Ампера и сила Лоренца
- •Силу (14.4) называют силой Лоренца. Ее величина
- •14.2. Закономерности движения заряженных частиц в магнитном поле
- •14.3. Ускорители заряженных частиц
- •Внутри дуанта электрическое поле отсутствует, поэтому
- •Контур с током в магнитном поле
- •В неоднородном магнитном поле помимо вращательного момента, стремящегося повернуть виток, будет действовать сила, вызывающая поступательное перемещение витка с током.
- •Если в процессе перемещения сила тока не меняется, то
- •14.5. Физические принципы работы электроизмерительных приборов
- •14.5.1. Магнитоэлектрическая система
- •Таким образом,
- •14.5.2. Электродинамическая система
- •§15. Электромагнитная индукция
- •Явление электромагнитной индукции. Закон Фарадея. Правило Ленца
- •Если потоки, пронизывающие витки, одинаковы, то
- •15.2. Генераторы и электродвигатели
- •15.2.1. Генератор переменного тока
- •15.2.2. Генератор постоянного тока и электродвигатель
- •Токи Фуко
- •15.4. Явление самоиндукции. Индуктивность
- •Потокосцепление самоиндукции такого соленоида
- •15.5. Токи при размыкании и замыкании цепи
- •15.6. Природа э.Д.С. Индукции
- •15.7. Явление взаимной индукци
- •15.8. Физические принципы работы трансформатора
- •§ 16.Энергия магнитного поля
- •16.1. Магнитная энергия контуров с током
- •16.2. Энергия магнитного поля. Плотность магнитной энергии
- •§ 17. Обобщение законов электромагнетизма. Уравнения Максвелла
- •17.1. Обобщение закона электромагнитной индукции. Первое уравнение Максвелла
- •17.2 Обобщение теоремы о циркуляции вектора напряженности магнитного поля. Ток смещения
- •17.3 Вектор плотности тока смещения
- •Таким образом, линии вектора плотности тока смещения между пластинами непрерывно переходят в линии плотности тока проводимости внутри проводящей пластины.
- •17.4. Второе уравнение Максвелла
- •17.5. Система уравнений Максвелла
12.7. Магнитное поле соленоида
С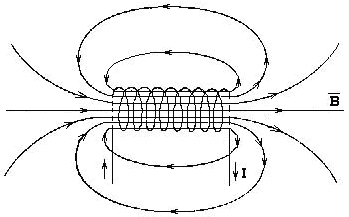 оленоид
представляет собой провод, навитый
равномерно в виде спирали на общий
цилиндрический каркас (см.
рис.
12.14).
Произведение (IN)
числа витков однослойной намотки
соленоида на силу тока, обтекающего
витки, называется числом ампер-витков.
оленоид
представляет собой провод, навитый
равномерно в виде спирали на общий
цилиндрический каркас (см.
рис.
12.14).
Произведение (IN)
числа витков однослойной намотки
соленоида на силу тока, обтекающего
витки, называется числом ампер-витков.
Рис. 12.14
Соленоиды
предназначены для создания в небольшом
объеме пространства достаточно сильного
магнитного поля. При плотной намотке
витков поле соленоида эквивалентно
полю системы круговых параллельных
токов с общей осью. Если диаметр d витков
соленоида во много раз меньше его длины
(d
l), то соленоид считается бесконечно
длинным (или тонким). Магнитное поле
такого соленоида практически целиком
сосредоточено внутри, причем вектор
магнитной индукции
![]() внутри
направлен
вдоль оси соленоида и связан с направлением
тока правилом правого винта.
внутри
направлен
вдоль оси соленоида и связан с направлением
тока правилом правого винта.
Р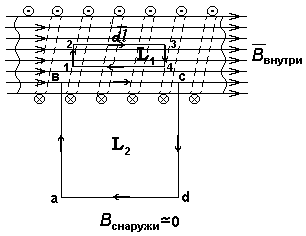 ис.
12.15
ис.
12.15
Рассмотрим
воображаемый замкнутый контур
![]() внутри соленоида (рис.
12.15). Этот
контур не охватывает токов, поэтому по
теореме о циркуляции
внутри соленоида (рис.
12.15). Этот
контур не охватывает токов, поэтому по
теореме о циркуляции
![]()
Разобьем
этот круговой интеграл на четыре
интеграла (по сторонам контура) и учтем,
что на отрезках (1-2) и (3-4) вектор
![]() перпендикулярен
перпендикулярен![]() ,
поэтому скалярное произведение (
,
поэтому скалярное произведение (![]() ,
,![]() )
здесь обращается в ноль. Индукция поля
во всех точках отрезка (2-3) одинакова и
равна
)
здесь обращается в ноль. Индукция поля
во всех точках отрезка (2-3) одинакова и
равна![]() 23,
а на отрезке (4-1)
23,
а на отрезке (4-1) ![]() 41,
причем l23 =
l41
= l.
41,
причем l23 =
l41
= l.
Таким образом, обойдя контур по часовой стрелке, получим
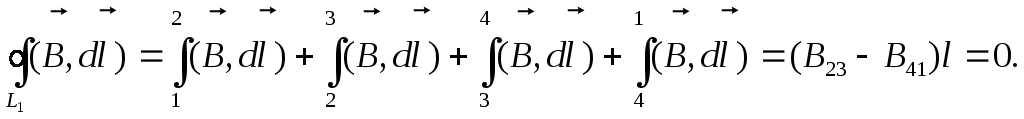
Так как l 0, то В23 = В41 = В внутри.
Поскольку контур внутри соленоида был выбран произвольно, то полученный результат справедлив для любых внутренних точек соленоида, то есть поле внутри соленоида однородное:
![]() внутри
= const.
внутри
= const.
Чтобы найти величину индукции этого поля, рассмотрим контур L2 (а –b –c –d –а ), охватывающий N витков с током (рис. 12.15). Согласно теореме о циркуляции (и на основании предыдущих рассуждений), получим соотношение
![]()
Поле
снаружи бесконечно длинного соленоида
очень слабое (![]() снаружи
=0), им можно
пренебречь, следовательно,
снаружи
=0), им можно
пренебречь, следовательно,
![]() (12.35)
(12.35)
где n=N/l - число витков, приходящихся на единицу
длины соленоида.
Таким образом, индукция магнитного поля внутри бесконечно длинного соленоида одинакова по величине и направлению и пропорциональна числу ампер-витков, приходящихся на единицу длины соленоида.
Симметрично расположенные витки вносят одинаковый вклад в магнитную индукцию на оси соленоида, поэтому у конца полубесконечного соленоида на его оси магнитная индукция равна половине того значения, которое дает формула (12.35), т.е.
![]() (12.36)
(12.36)
Практически, если (l d), то формула (12.35) справедлива для точек в средней части соленоида, а формула (12.36) – для точек на оси вблизи его концов.
Применяя закон Био-Савара-Лапласа, можно найти магнитную индукцию поля соленоида конечной длины (рис. 12.16) в произвольной точке А на его оси:
![]() (12.37)
(12.37)
г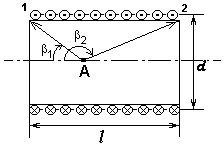 де
де![]() - углы между осью соленоида и радиус-
вектором, проведенным из рассматриваемой
точки к концам соленоида.
- углы между осью соленоида и радиус-
вектором, проведенным из рассматриваемой
точки к концам соленоида.
Рис. 12.16
Поле
такого соленоида неоднородное, величина
индукции зависит от положения точки А
и длины соленоида. Для бесконечно
длинного соленоида
![]() ,
,![]() ,
и формула (12.37) переходит в формулу
(12.35).
,
и формула (12.37) переходит в формулу
(12.35).
