16.2. Энергия магнитного поля. Плотность магнитной энергии

Возникает вопрос о том, где локализована энергия контура с током. Эта энергия не меняется, если не меняется ток в данном контуре, однако ее нельзя сопоставить непосредственно с кинетической энергией движения электронов в контуре, поскольку контур с другой индуктивностью при том же токе будет иметь другую энергию.

Исследование свойств переменных магнитных полей показало, что энергия магнитного поля локализована в пространстве. Энергия элемента объема dV поля равна

(16.3)

где - плотность энергии магнитного поля, т.е. энергия единицы объёма магнитного поля.

Для вычисления этой характеристики рассмотрим простейший случай однородного поля внутри длинного соленоида. Подставив в формулу (16.1) выражение (15.11), получим магнитную энергию поля соленоида

(16.4)

Поскольку индукция магнитного поля внутри такого соленоида равна

(16.5)

то, подставив (16.5) в (16.4), получим

(16.6)

Поскольку произведение lS=V -объем однородного магнитного поля соленоида, то из сопоставления формул (16.6) и (16.3), с учетом формулы =, получим для объемной плотности магнитной энергии три эквивалентных формулы:

(16.7)

Выведенные для случая однородного поля эти выражения остаются справедливыми и для неоднородных полей.

В электростатике были получены аналогичные формулы для объемной плотности энергии электрического поля (§ 3):

При наличии в пространстве и электрического и магнитного поля объёмная плотность энергии равна

Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенную в любом объёме V. Для этого надо вычислить интеграл:

§ 17. Обобщение законов электромагнетизма. Уравнения Максвелла

17.1. Обобщение закона электромагнитной индукции. Первое уравнение Максвелла

В § 15 отмечалось, что в явлении электромагнитной индукции электродвижущая сила зависит только от скорости изменения магнитного потока. Изменение магнитного потока может быть вызвано движением контура в стационарном магнитном поле, либо изменением во времени магнитного поля, если контур неподвижен. С учетом двух возможностей изменения потока магнитной индукции закон Фарадея может быть записан в обобщенной форме:

. (17.1)

Соотношение (17.1) первоначально было получено Максвеллом экспериментально для контура из тонкого проводника.

В этом частном случае Э.Д.С. индукции создает в проводнике электрический ток, который можно измерить прибором, включенным в контур, и тем самым обнаружить индуктированное переменным магнитным полем электрическое поле .

Таким образом, в явлении электромагнитной индукции проводящая цепь и возбуждаемый в ней ток не имеют принципиального значения.

Необходимо отметить, что обобщенный закон электромагнитной индукции (17.1) справедлив лишь для произвольного материального контура L.

При вычислении изменения потока магнитной индукции через опирающуюся на контур поверхность S необходимо считать, что в момент времени (t+dt) контур образуется теми же материальными точками среды, которыми он был образован в момент t. Поэтому при рассмотрении электромагнитных процессов в контурах, которые движутся вместе с вещественной средой относительно системы в которой измеряется поле, необходимо использовать обобщенный закон электромагнитной индукции в форме (17.1).

При исследовании электромагнитных процессов в средах, в которых контур покоится , формула (17.1) упрощается:

(17.2)

Закон (17.2), обобщенный на случай произвольного замкнутого контура, который может быть и воображаемым, проходящим через любые среды, называют первым уравнением Максвелла в интегральной форме.

Этот закон характеризует процессы, происходящие непосредственно в электромагнитном поле. В соответствии с (17.2) изменяющееся во времени магнитное поле порождает в той же области пространства электрическое поле.

Электрическое поле по своим свойствам отличается от электростатического поля, созданного неподвижными зарядами. Действительно, из теоремы Гаусса-Остроградского для вектора электрического смещения

следует, что источником электростатического поля являются заряды, причем силовые линии поля начинаются на положительных зарядах и заканчиваются на отрицательных.

Циркуляция вектора по любому замкнутому контуру равна нулю, что является следствием потенциальности электростатического поля.

В отличие от поля , электрическое поле, созданное изменяющимся во времени магнитным полем, согласно (17.2) имеет отличную от нуля циркуляцию и, следовательно, являетсявихревым. Силовые линии такого поля замкнуты.

Из (17.2) так же следует, что циркуляция вектора напряженности вихревого электрического поля по произвольно выбранному контуру равна взятой со знаком минус скорости изменения магнитного потока через поверхность, опирающуюся на контур.

И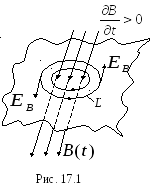сходя из закона Фарадея, можно дать интерпретацию первого уравнения Максвелла в интегральной форме:изменяющийся во времени магнитный поток через нормальную к нему воображаемую поверхность создает вихревое электрическое поле, направление силовых линий которого на поверхности определяется по правилу Ленца (рис. 17.1).

Правило Ленца утверждает, что должен создаваться новый магнитный поток, препят-ствующий изменению внеш-него магнитного потока.

Если среда, в которой выбран воображаемый контур L не является проводящей, то остается заключить, что новый магнитный поток (а, следо-вательно, и создающее его магнитное поле) должен порождаться вихревым электрическим полем. Это предположение лежит в основе второго уравнения Максвелла, которое будет рассмотрено ниже.