Глава III. Магнетизм

§12. Магнитное поле в вакууме

12.1. Опыт Эрстеда. Индукция магнитного поля

Начало исследований электромагнитных явлений было положено опытом датского профессора Г.Х. Эрстеда. В 1820 году Эрстед обнаружил, что на магнитную стрелку, помещенную вблизи провода с током, действует сила. Под действием этой силы стрелка, поворачиваясь вокруг вертикальной оси, стремится расположиться перпендикулярно проводу с током (рис. 12.1).

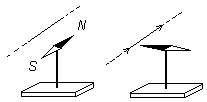
Рис. 12.1

Ось стрелки ( N–S ) тем точнее совпадает с этим направлением, чем больше сила тока I и чем слабее влияние магнитного поля Земли. Направление поворота северного полюса (N) стрелки под действием тока меняется на противоположное при изменении направления тока в проводе.

Дальнейшие исследования показали, что электрические токи (или движущиеся заряды) порождают в окружающем пространстве силовое поле, полностью идентичное по свойствам полю постоянных магнитов – магнитное поле.

Термин «магнитное поле» впервые ввел в 1845 году М. Фарадей. В настоящее время доказано, что источниками постоянного магнитного поля являются стационарные (т.е. не перемещающиеся в пространстве) электрические токи любой природы (в металлических проводниках, в газах, в электролитах и т.п.). Поле постоянных магнитов обусловлено циркулирующими в их толще микроскопическими замкнутыми токами, а также наличием у микрочастиц собственных (спиновых) магнитных моментов (см. п. 13.1).

Наличие магнитного поля можно обнаружить по действию сил на внесенные в него постоянные магниты (намагниченные тела), проводники с током или движущиеся заряды: магнитная стрелка, например, будет устанавливаться своей осью по направлению магнитного поля (рис. 12.2, а).

Для изучения свойств магнитного поля, в частности, его величины и направления, используется замкнутый плоский контур с током (рамка с током). Форма контура не имеет значения, а его размеры должны быть малы по сравнению с расстоянием до источников магнитного поля (пробный контур). Контур с током принято характеризовать магнитным моментом

(12.1)

где I - сила тока, обтекающего контур,

S - площадь поверхности контура,

- единичный вектор нормали к контуру, образующий

с направлением тока правовинтовую систему

(рис. 12.2).

Направление `вектора совпадает с направлением вектора нормали.

Если внести пробный контур в однородное магнитное поле, направление которого не совпадает с направлением, (рис. 12.2, б), то возникает вращающий момент сил , который стремится повернуть контур вокруг осиО^'О, перпендикулярной и полю. В результате плоскость контура установится перпендикулярно направлению поля, а векторукажет направление поля. Таким образом, магнитное поле оказывает на контур ориентирующее действие.

Магнитное поле

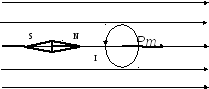
а)

б)

Рис. 12.2

Опыт показывает, что вращающий момент сил зависит как от свойств поля в данной точке, так и от величины и ориентации магнитного момента контура: если угол  между и направлением поля равен нулю, то и= 0 (положение равновесия контура в поле), если=, тоМ = M_max. Внося в одну и ту же точку поля различные пробные контуры, обнаружим, что M_max  Р_m , однако отношение М_max / Р_m не зависит от свойств контура и может служить количественной силовой характеристикой магнитного поля в данной точке. Эта величина называется вектором магнитной индукции . Его модуль равен отношению

(12.2)

Направление вектора совпадает с направлением вектора контура в его устойчивом положении равновесия в поле.

Таким образом, согласно формуле (12.2), магнитная индукция в данной точке однородного магнитного поля численно равна максимальному вращающему моменту сил, действующему на пробный контур с единичным магнитным моментом.

Единица магнитной индукции в системе СИ - тесла (Т):

1 Т =

Аналогично электрическому, стационарное магнитное поле можно наглядно изображать с помощью линий магнитной индукции – силовых линий.. Касательная к силовой линии в каждой ее точке показывает направление вектора в этой точке. Густота силовых линий , пропорциональна величине индукции поля в данной области (как и для электростатического поля): в местах увеличения силовые линии сгущаются, в местах ослабления – разрежаются. В однородном магнитном поле силовые линии вектора имеют вид системы прямых линий, равноотстоящих друг от друга.

Определить вид линий вектора можно по ориентации в разных точках поля магнитной стрелки или пробного контура с током. Линии можно также «проявить» при помощи железных опилок. Опыт показывает, что силовые линии вектора магнитного поля всегда замкнуты(нигде не прерываются) и охватывают токи – это их отличительная особенность по сравнению с силовыми линиями электростатического поля, которые начинаются на положительных и заканчиваются на отрицательных зарядах.

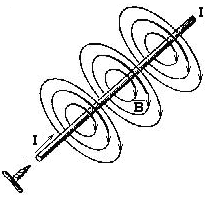
Рис. 12.3

Направление линий индукции определяется правилом правого буравчика (см. рис. 12.3): если ввинчивать буравчик по направлению линий тока в проводнике, то направление движения рукоятки буравчика укажет направление линий магнитной индукции.