29. Векторное произведение, смешанное произведение векторов. Их геометрический смысл.

Векторное произведение векторов и его свойства.

Векторным произведением вектора а на b называется вектор с, который

1) перпендикулярен векторам а и b

2) имеет длину численно равную площади параллелограмма, построенного на векторах а и b.

С │c│=│a││b│sinφ

B S

φ

b

3)Вектора a,b,c образуют правую тройку

а × b; [a,b]

0

Из определения векторного произведения непосредственно вытекают следующие отношения между ортами i, j,k

i × j = k ; j × k = i ; k × i = j

Докажем, например, что i × j = k:

1)k перпендикулярен к i; k перпендикулярен к j

2)│k│=1, но │i × j │=│i│×│j│sin90⁰ = 1

3) вектора i, j, k образуют правую тройку

Три некомпланарных вектора a, b, с образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b.

правая тройка левая тройка

с с

а b а b

Свойства векторного произведения:

1) при перестановке сомножителей, векторное произведение меняет знак.

a×b a×b = - b×a

S Вектора a×b и b×a коллинеарны, имеют одинаковые модули (S

параллелограмма остается неизменной), но противоположно

направлены.

b×a

2) Векторное произведение обладает сочетательным свойством, относительно скалярного множителя.

λ(a×b) = (λ a)×b = (a×λ b)

Доказательство:

Пусть λ›0 ; λ(a×b) перпендикулярен а и b, вектор (λ a)×b также перпендикулярен а и b. Вектора а и λ a лежат в одной плоскости. Значит вектора λ(a×b) и (λ a)×b коллинеарны. Очевидно, что их направления совпадают, имеют одинаковую длину.

│λ(a×b) │= λ│a×b│=λ│а││b│sin(a,b)

│(λ a)×b│= │λ a││b│sin(λ a,b) = λ│a││b│sin(a,b)

Поэтому λ(a×b) = λ a×b

Аналогично доказывается при λ‹0

3) Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно ненулевому вектору, то есть:

а || b <=> a×b = 0

4) (a + b)c = ac + bc

Векторное произведение через координаты.

Будем использовать таблицу векторного произведения векторов i, j, k

	i	j	k
i	0	k	j
J	-k	0	i
k	i	-j	0

i

k j

Если направление кратчайшего пути совпадает с направлением стрелки, то произведение равно третьему вектору.

а = а_хi + а_yj + а_zk и b = b_хi + b_yj + b_zk.

a×b = (а_хb_z – а_zb_y)i - ( a_хb_z – a_zb_x)j +( a_хb_y – a_yb_x)k =

Смешанные произведения векторов.

Определение смешанного произведения,

его геометрический смысл.

Рассмотрим произведение векторов a, b, c, составленное следующим образом: (a×b)∙с –

здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным или смешанным произведением трех векторов. Смешанное произведение представляет собой некоторое число. Выясним геометрический смысл выражения (a×b)∙с

d

H c

b S

Имеем: (a×b)∙с = │d│пр_dс ; │d│= │a×b │= S

Таким образом смешанное произведение трех векторов равно объему параллепипеда, построенного на этих векторах. Взятых со знаком «+», если они образуют правую тройку и со знаком «-», если левую тройку.

Свойства смешанного произведения:

1) Смешанное произведение трех векторов равно 0, если

а) хотя бы один из векторов равен 0

б)два из перемножаемых вектора коллинеарны

в)три ненулевых вектора параллельны одной и той же плоскости (компланарны)

2) Смешанное произведение не изменится, если в нем поменять местами знаки векторного и скалярного:

(a×b)с = a (b×с)

3) При перестановке любых двух векторов смешанное произведение изменяет только знак:

bac=-abc; cba=-abc; acb=-abc

а = а_хi + а_yj + а_zk

Выражение смешанного произведения через координаты.

Пусть заданы вектора: а = а_хi + а_yj + а_zk , b = b_хi + b_yj + b_zk и с = с_хi + с_yj + с_zk

Найдем их смешанное произведение, используя выражение в координатах для векторного и скалярного произведений:

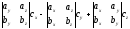= (1)

Полученную формулу можно записать в виде:

Следовательно, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.