
- •Определители 2го и 3го порядка. Решение систем линейных уравнений из 2х и 3х уравнений
- •Определители n-ного порядка. Их элементарные свойства
- •Разложение определителя по строке
- •Линейные системы n-го порядка. Правило крамера
- •Матрицы. Их виды и операции с ними(сложение, умножение, умножение на число и транспонирование)
- •Обратная матрица
- •Матричные уравнения
- •Решение линейных систем n-го порядка в матричном виде(в терминах обратной матрицы)
- •Линейная зависимость(независимость) столбцов матрицы. Ранг матрицы.
- •Теорема о базисном миноре
- •Методы вычисления ранга матрицы и нахождения базисного минора
- •Линейные системы уравнений общего вида. Их элементраные преобразования. Метод гаусса решения таких систем.
- •Однородные системы уравнений. Ранг матрицы и существование нетривиального решения.
- •Структура общего решения однородной системы уравнений.
- •Неоднородные системы уравнений общего вида. Теорема Кронекера-Капелли
- •Строение множества решений неоднородной системы уравнений общего вида.
- •Векторное пространство. Операции над векторами. Линейная независимость
- •Базис пространства. Размерность пространства
- •Связь между различными базисами.
- •Преобразование координат при замене базиса.
- •Линейные операторы и их матричная форма.
- •Действия с линейными операторами.
- •Преобразование матрицы линейного оператора при переходе к новому базису.
- •Собственные числа и собственные вектора линейного оператора
- •Переход к базису собственных векторов, когда все собственные числа различны.
- •Квадратичные формы. Приведение к диагональному виду
- •Инерция квадратичных форм
- •Скалярное произведение векторов. Длина вектора. Проекция вектора на ось. Угол между векторами.
- •Векторное произведение, смешанное произведение векторов. Их геометрический смысл.
- •Линии второго порядка на плоскости.
- •Прямая на плоскости
- •Элипс, ее директриссы
- •Гипербола, ее директриссы
- •Парабола
- •Уравнение кривых второго порядка в полярных координатах.
- •Плоскость в пространстве
- •Прямая в пространстве
- •Прямая и плоскость. Две плоскости в пространстве
- •Две прямые, точка и плоскость, точка и прямая в пространстве
- •Поверхности второго порядка в пространстве
-
Гипербола, ее директриссы
Гипербола.
Гиперболой называется
множество всех точек плоскости, модуль
разности расстояний от каждой из которых
до двух точек этой плоскости, называемых
фокусами, есть величина постоянная,
меньшая чем расстояние между фокусами.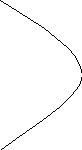
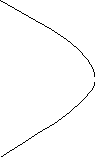
y




M(x;y)
F(-c;0) F(c;0) x
x=-a x=a
Согласно определению гиперболы │МF1│-│MF2│ = 2а, то есть

После упрощений, как это было при выводе уравнения эллипса, получим каноническое уравнение гиперболы:
 (7)
(7)
b2 = c2 – a2 (8)
-
Парабола
Парабола.
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается буквои Р(Р>0). Для вывода уравнения параболы выберем систему координат Оху, так чтобы ось Ох проходила через фокус F.

N
M(x;y)


x=-P/2 0 x F(P\2;0) x
По
определению параболы МF
= MN,
по формуле расстояний между двумя
точками находим: отсюда получаем:
отсюда получаем:
 (9)
(9)
Это и есть каноническое уравнение параболы.
Пример: из уравнения (1) можно определять:
при А=С – окружность
АС>0 – эллипс
АС<0 – гипербола
АС=0 – парабола
Пример: установить вид прямой 2 –ого порядка, заданной уравнением 4х2+5у2-20х-
-30у+10=0
Решение: А=4 С=5 АС=4∙5=20>0 – следовательно это эллипс
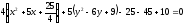


 Центр эллипса
-
Центр эллипса
-

Пример 2: х2+10х-2у+11=0 С=0 АС=0 следовательно парабола
х2+10х-2у+11+25-25=0
(х+5)2 = 2у+14
(х+5)2=2(у+7) – уравнение параболы
О(-5;7) – вершина параболы ; Р=1
-
Уравнение кривых второго порядка в полярных координатах.
Кривой второго порядка на плоскости называют множество точек (х, у) удовлетворяющие:
Ax
 +
2Bxy + Cy
+
2Bxy + Cy
 + 2Dx + 2Ey + F = 0 (a)
+ 2Dx + 2Ey + F = 0 (a)
Сдвиг начала координат
x=х’ +a y=y’ +b a и b const
Получаем такое же уравнение (а) только с другими коэффициентами
Поворот
системы координат
X=
x’cos

 – y’
sin
– y’
sin


Y=
x’sin
 + y’
cos
+ y’
cos


При повороте уравнение (а) остаётся, только с другими коэффиц.
Можно ли с этими процедурами упростить А?
С помощью поворота:
A(x’cos

 – y’sin
– y’sin

 )
)
 + 2B(x’cos
+ 2B(x’cos
 – y’sin
– y’sin
 )*(x’sin
)*(x’sin
 + y’cos
+ y’cos
 +
C(x’sin
+
C(x’sin
 + y’cos
+ y’cos
 2+.
. . =
2+.
. . =
x’y’(-2Acos
 sin
sin
 + 2cos
+ 2cos
 sin
sin
 +
2B(cos2
+
2B(cos2
 – sin2
– sin2
 )
+ . . . = x’y’[sin2
)
+ . . . = x’y’[sin2
 (C-A)+2Bcos2
(C-A)+2Bcos2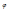
 ]+.
. .
]+.
. .
нужно обнулить это уравнение
(C
– A)sin2
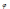 = 2B
cos
= 2B
cos
 tg
2
tg
2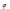
 =
= 

Tg принимает любое значение, поэтому это уравнение имеет решение при любой кривой части, следовательно, Bxy можно устранить с помощью поворота
Ax2 +Cy2 + 2Dx + 2Ey +F = 0 (b)
Если
АС 
 0 то можно устранить Е и С
0 то можно устранить Е и С
A(x
+ 
 )2
+ C(y
+
)2
+ C(y
+ 
 )2
+F2
= 0
)2
+F2
= 0
Можно
написать: x’
= x
+ 


y’
= y
+ 
 сдвиг начала системы координат
сдвиг начала системы координат
Ax2 + Cy2+ F = 0 (c)
A,C,F
– одного знака, тогда 
 +
+ 
 = -1 F
переношу направо и делю на F,
получаем уравнение мнимого элипса
= -1 F
переношу направо и делю на F,
получаем уравнение мнимого элипса
