6. Обратная матрица

Матрица А^-1 называется обратной матрице А, если А∙А^-1 = А^-1∙А = Е, где Е – единичная матрица такого же порядка

Теорема.

Всякая невырожденная матрица имеет обратную. Приведем доказательство для 3 –ого порядка:

det A ≠ 0

Найдем А×А^*:

Итак получим: А∙А^* = detA∙Е

Аналогично убеждаемся что: А^*∙А= detA∙Е

Отсюда находим Е:

Сравнивая полученные результаты, получим:

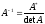, то есть

Отметим свойства обратной матрицы:

1. det(A^-1)=1/detA

2. (AB) = B^-1A^-1

3. (A^-1)^T = (A^T)^-1

7. Матричные уравнения

Матричные уравнения могут иметь вид:

АХ = В, ХА = В, АХВ = С,

где А,В,С — задаваемые матрицы, Х- искомая матрица.

Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.

Например, чтобы найти матрицу  из уравнения , необходимо умножить это уравнение на  слева.

Тогда:

Следовательно, чтобы найти решение  уравнения 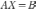, нужно найти обратную матриц и умножить ее на матрицу , стоящие в правой части уравнения.

Аналогично решаются другие уравнения.

8. Решение линейных систем n-го порядка в матричном виде(в терминах обратной матрицы)

Справедливо следующее утверждение (формулы Крамера).

Если определитель D=det A матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x₁ , x₂ , ..., x_n, определяемое формулами Крамера

x_i =D_i / D, i=1,2, ..., n,

где D_i - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом правых частей b.

 

ПРИМЕР 2. Вычисление решения системы линейных уравнений по формулам Крамера.

 

Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x₁ , x₂ , ..., x_n

приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей

решение которой находят по рекуррентным формулам:

x_n =d_n , x_i = d_i -S ⁿ_k=i+1 c_ik x_k , i=n-1, n-2, ...,1.

Матричная запись метода Гаусса.

1. Прямой ход метода Гаусса: приведение расширенной матрицы системы

    к ступенчатому виду

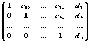            с помощью элементарных операций над строками матрицы (под элементарными операциями понимаются следующие операции:

• перестановка строк;

• умножение строки на число, отличное от нуля;

• сложение строки матрицы с другой строкой, умноженной на отличное от нуля чиcло).

Обратный ход метода Гаусса: преобразование полученной ступенчатой матрицы к матрице, в первых n столбцах которой содержится единичная матрица  ,  последний, (n+1)-й, столбец этой матрицы содержит решение системы.

9. Линейная зависимость(независимость) столбцов матрицы. Ранг матрицы.

Ранг матрицы.

Рассмотрим матрицу А, размером m×n:

Выделим в ней К строк и К столбцов, где К ≤ min(n;m). Из элементов стоящих на пересечении выделенных строк и столбцов составим определитель К –ого порядка. Все такие определители называются минорами этой матрицы. В матрице А пунктиром выделим этот минор. В данный момент – это минор 2 –го порядка. Заметим, что таких миноров можно составить . С – комбинация, где:

;

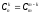
Пример:

миноров

Наивысший порядок миноров матрицы, отличительных от 0 называется рангом матрицы.

Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров. Ранг матрицы обозначают r(A), rang(A)

Основные свойства ранга матрицы:

1. при транспонировании матрицы, её ранг не меняется

2. если вычеркнуть из матрицы нулевой ряд, то её ранг не изменится

3. ранг матрицы не изменится при элементарных преобразованиях матрицы

Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.