3.10. Параллельное соединение приемников электроэнергии

При параллельном соединении приемников общий ток в неразветвленной части определяется по I закону Кирхгофа как векторная сумма токов отдельных приемников:

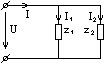
Возьмем для простоты два параллельно соединенных приемника:

Y₁(q₁,b₁) и Y₂(q₂,b₂) (рис. 3.23).

Тогда:

. (3.49)

По уравнению (3.49) построим для расчетной схемы векторную диаграмму, приняв за исходный вектор напряжение . Затем, на диаграмме, разложим каждый вектор тока на активную и реактивную составляющие (рис. 3.24).

Рис. 3.23

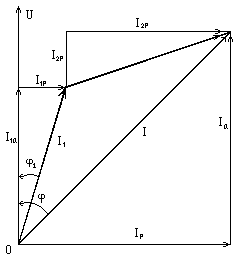
Рис. 3.24

Из диаграммы очевидны соотношения:

(1) - арифметическая сумма;

(2) - алгебраическая сумма;

(3) - векторная сумма.

Заменив токи произведениями напряжения U на соответствующие проводимости, по закону Ома имеем:

Здесь:

- арифметическая сумма; - алгебраическая сумма, ; - векторная сумма полных проводимостей.

Величину Y можно было бы найти иначе:

.

Произведенный вывод можно распространить на любое число параллельно соединенных приемников, а именно: активные проводимости складывается арифметически; реактивные – алгебраически; полные – как вектора.

Рассмотрим пример в общем виде (3.25), когда заданы полные сопротивления параллельных ветвей, а не их проводимости.

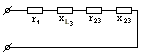
		z1(r1,xL1), z2(r2,xc2).			Последовательность преобразования схем следующая (рис.3.26):
Рис.3.25		I=? Cosφ=?
а)		q=q+q, б) в=в+в.

в) г)

Рис. 3.26

; ;;

; (+) ; () ;.

3.11. Смешанное соединение приемников

Это соединение рассмотрим на примере в общем виде (рис. 3.27):

Рис. 3.27

Дано: U; z₁ (r₁, x_L1);

z₂ (r₂, x_c2); z₃ (r₃, x_L3).

Найти: I₁; I₂; I₃; U₁; U₂₃=U_ab.

Построить: топографическую векторную диаграмму.

I. Преобразование схемы.

Вначале найдем величины полных сопротивлений: ; ;.
	; ;	. () . (+)
	; ; .
	; ; .	; ; .

II. Нахождение величины токов и напряжений:

; ;;;.

Рис. 3.28

III. Построение топографической векторной диаграммы.

Исходный вектор (рис. 3.28). Используя треугольники сопротивлений (r₂; x_c2) и (r₃; x_L3) строим I₂ и I₃. По I закону Кирхгофа строим . Используя (r₁; x_L1) строим напряжение U₁.

По II закону Кирхгофа: . Раскладываемина активные и реактивные составляющие, получаем точки: а, в,m, n, K. Расстояние между ними в масштабе равны соответствующим напряжениям: