Контрольные вопросы и задания

1. Дайте определение нерегулярностям в ЛП.

2. Опишите влияние нерегулярностей на распространение ЭМВ в ЛП?

3. Как определяется волновое сопротивление для волноводов?

4. Как определяют КПД линии передачи?

5. Опишите явление трансформации сопротивлений в линии передачи.

6. Опишите поведение сопротивления линии при ее коротком замыкании.

7. Опишите поведение сопротивления разомкнутой линии.

8. Дайте определение свойству четвертьволновой трансформации.

9. Приведите примеры эквивалентных емкостей и индуктивностей в линиях.

10. Дайте определение декомпозиции, матрицам рассеяния и передачи.

11. Как зависят коэффициенты отражения и передачи от длины линии?

12. Дайте определение и объясните особенности ЭМП стоячей ЭМВ.

13. Дайте определение и укажите область значений КСВ и КБВ.

14. Почему нежелательно появление стоячей ЭМВ в линии?

15. Опишите методику работы с диаграммой Смита – Вольперта.

16. Как на практике используют явление трансформации сопротивлений?

17. Назовите основные критерии согласования.

18. Дайте характеристику узкополосному и широкополосному согласованию.

19. Как отражения ЭМВ от нагрузки влияют на характеристики ЛП?

Тема 20. Элементы линий передачи

Матричные методы описания элементов ЛП и СВЧ-устройств. Эквивалентные схемы неоднородностей (нерегулярностей) в ЛП. Матрицы сопротивлений, проводимости, рассеяния и передачи.

Возбуждение ЭМВ в ЛП. Возбудители типов волн. Сочленения и изгибы линий передачи. Трансформаторы и фильтры типов волн. Короткозамкнутые поршни. Согласованные нагрузки. Разветвления ЛП. Направленные ответвители. Двойной волноводный тройник. Управление амплитудой, фазой и поляризацией ЭМВ в ЛП. Аттенюаторы, фазовращатели, поляризаторы.

Конструктивные неоднородности: диафрагмы, реактивные штыри, шлейфы, стыки линий с разными поперечными размерами.

Указания к теме

Необходимо изучить основные разновидности возбуждающих элементов, неоднородностей в ЛП, устройств СВЧ основных классов. Для СВЧ-устройств, указанных в теме, необходимо описать конструкцию, привести основные параметры, указать область применения.

Необходимо изучить основные виды конструктивных неоднородностей в ЛП, уметь описывать вносимые ими эффекты.

При изучении вопросов согласования ЛП следует обратить внимание на критерии согласования, возможные искажения сигналов, на принципиальные отличия узкополосных и широкополосных устройств.

Основные сведения

В диапазоне ОВЧ и выше условие квазистационарности не выполняется, и ЭМПпроявляетволновойхарактер[33, 37].

Для расчетов УВЧ и СВЧ многополюсников (рис. 20.1) обычно используют волновые матрицы, связывающие приведенные напряжения падающих и отраженных волн на входах многополюсника.

Под приведенным напряжением V, характеризующим энергетические соотношения ЭМВ в плечах многополюсника, понимают напряжение U в ЛП, деленное на ее :

[37]

Матрицы сопротивлений (Z-матрица) и проводимости (Y-матрица) выражают связь напряжений и токов многополюсника :

; ;, (20.1)

Для четырехполюсников (элементы Z-матрицы определяются при холостом ходе, а Y-матрицы – при коротком замыкании входов) [37]:

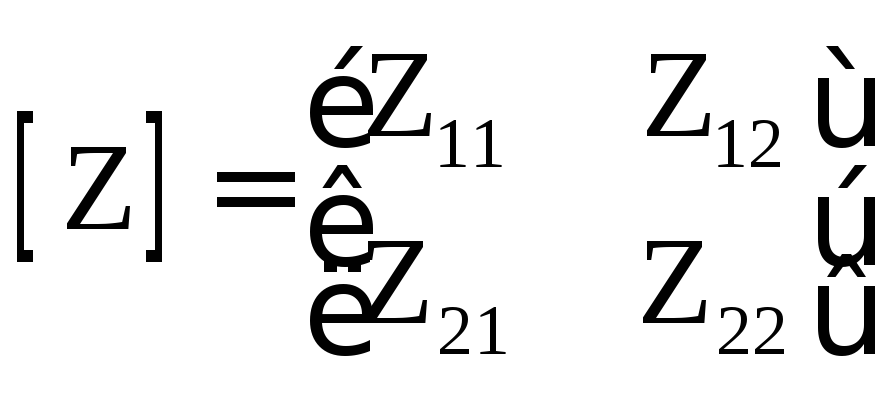; . (20.2)

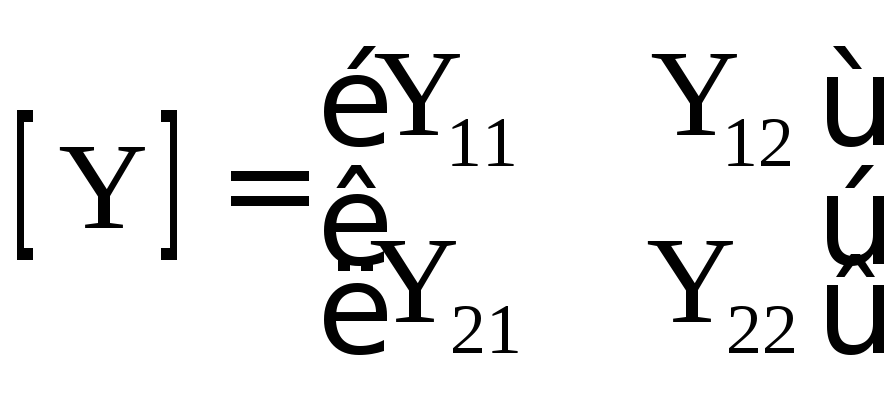; . (20.3)

Достоинством Z- и Y-матрицы является возможность простого представления сосредоточенных нерегулярностей в регулярной ЛП [2].

Волновой характер ЭМП в диапазонах УВЧ и СВЧ затрудняет применение Z- и Y-матриц из-за явления трансформации сопротивлений и проводимостей в ЛП. Эти матрицы могут быть рассчитаны только для определенных сечений ЛП, и при неудачном выборе плоскости отсчета элементы матриц могут принимать бесконечно большие значения.

Поэтому для анализа удобно использовать матрицы с волновыми величинами, которые не изменяют свой модуль в ЛП без потерь [2, 37].

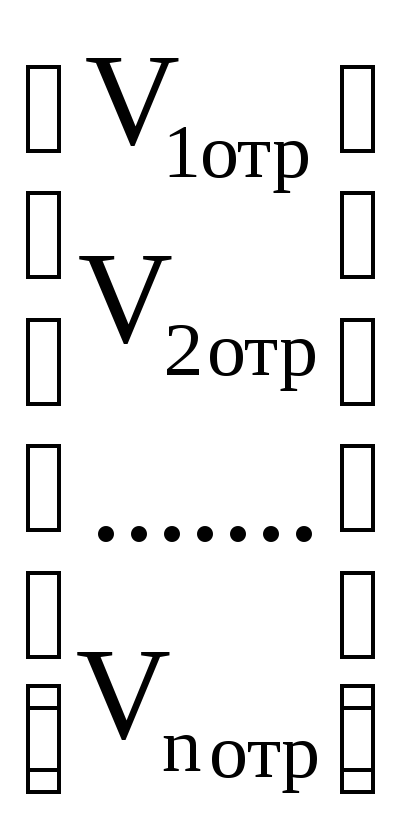
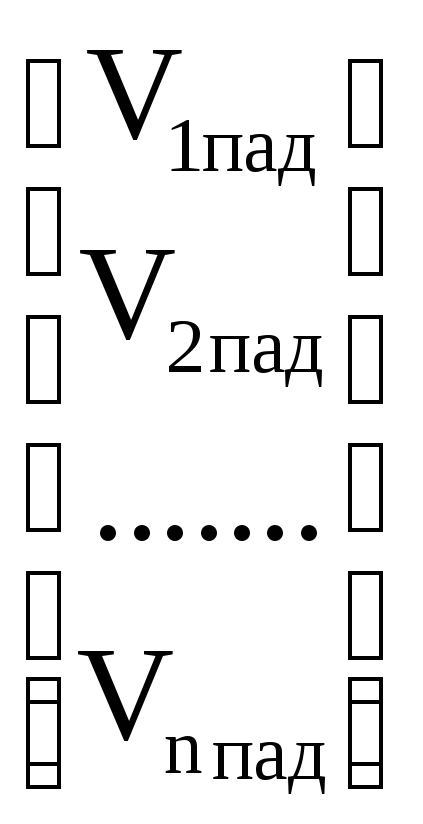
Такими матрицами являются матрица рассеяния (S-матрица) и матрица передачи (T-матрица). Используя элементы волновой матрицы рассеяния (S-параметры), связь между приведенными напряжениями падающих и отраженных волн можно представить в следующем виде:

, где . (20.4)

Элементы S-матрицы имеют ясный физический смысл: S_ii является коэффициентом отражения i-го плеча, а S_ki (при i  k) – коэффициентом передачи с i-го входа на k-й выход по приведенному напряжению V.

Если S-матрица устройства известна, то можно считать, что оно описано полностью [2, 33, 37]. Значения элементов матрицы рассеяния могут быть определены экспериментально. Элементы матрицы рассеяния не зависят от того, какие в дальнейшем внешние нагрузки и источники будут подключаться к плечам. S-матрица изменяется только со сменой типа волны или значений параметров элементов.

Во взаимных устройствах с линейными изотропными средами матрица рассеяния симметрична: S_ki = S_ik [37]. Важными являются следующие свойства S-матрицы для пассивных устройств без потерь [37]:

; (20.5)

. (20.6)

Свойство (20.5) выражает закон сохранения энергии.

S-матрица, удовлетворяющая условиям (20.5) и (20.6), называется унитарной. Число ее независимых элементов составляет N(N+1)/2, а для взаимных устройств: N(N–1)/2.

В технике УВЧ и СВЧ широко распространены четырехполюсники, которым соответствует матрица рассеяния

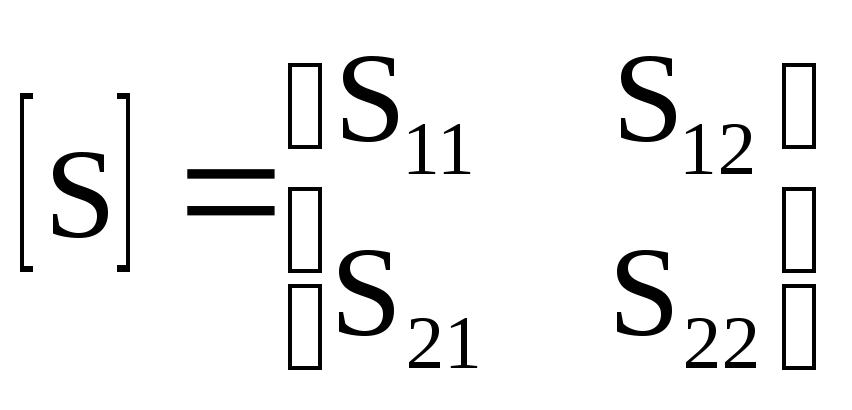. (20.7)

Элементы этой матрицы (S-параметры) принято называть так: S₁₁ и S₂₂  коэффициент отражения от входа и выхода соответственно; S₂₁  коэффициент прямой передачи; S₁₂  коэффициент обратной передачи.

В случае взаимного устройства без потерь у матрицы (20.7) будет только один независимый элемент. Связывая S-параметры (20.7) между собой с помощью (20.5) и (20.6), получим

; . (20.8)

При каскадном соединении многополюсников итоговая матрица рассеяния не может быть получена простым перемножением матриц БЭ. В этом случае удобно использовать матрицу передачи (T-матрицу), которая не имеет данного недостатка. При расчетах каскадного соединения четырехполюсников с матрицами передачи [T₁][T₂],…,[T_n] результирующая матрица передачи равна произведению их матриц передачи: [T_]=[T₁][T₂]…[T_n]. Элементы [S] и [T] матриц связаны так [37]:

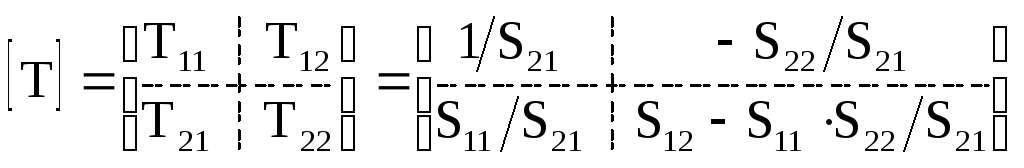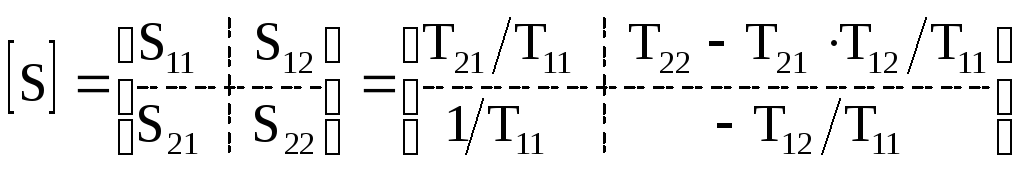; . (20.9)

При объединении S-матриц каскадного соединения четырехполюсников возможен переход от S-матриц к T-матрицам (20.9), а после получения итоговой T-матрицы – обратный переход к матрице рассеяния.

Аналогичная связь S-матрицы с Z- и Y-матрицами определяется так:

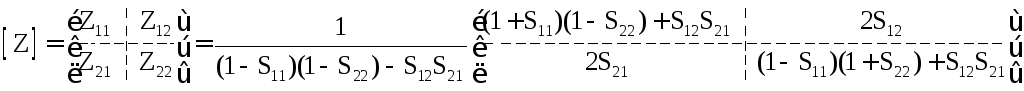; (20.10)

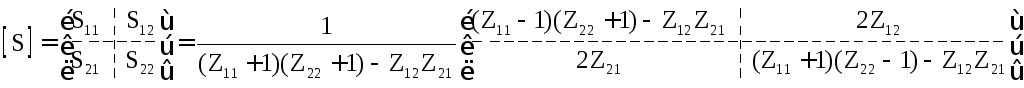. (20.11)

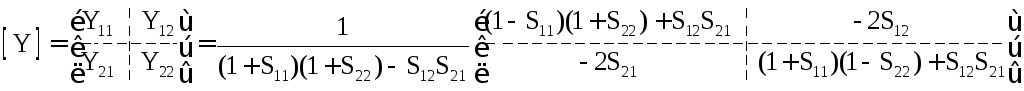; (20.12)

. (20.13)

Переход от S-матрицы к T, Z и Y-матрицам и обратно возможен не всегда. Математически условия допустимости преобразований (20.9) (20.13) можно сформулировать так: знаменатель общего множителя в соответствующей формуле должен иметь ненулевое значение.

Методы анализа многоэлементных устройств СВЧ основаны на расчленении (декомпозиции) сложного объекта на отдельные более простые, S-матрицы которых могут быть рассчитаны сравнительно просто. Затем по определенным алгоритмам (рекомпозиция) находится S-матрица устройства в целом.

Э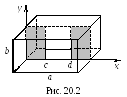МВ в ЛП возбуждают с помощью штырей, петель связи, отверстий связи и т. п. В каждом случае оптимальное место ввода устройства возбуждения строго определено [2, 33].

Нерегулярности в волноводе. Рассмотрим диафрагмы в прямоугольном волноводе (рис. 20.2). Эти диафрагмы вносят в ЭМП реактивность, которую учитывают как сосредоточенную нерегулярность, вклю­ченную параллельно в регулярную ЛП [22].

Тонкаяиндуктивная диафрагма (рис. 20.3) образована металлическими пластинами, примыкающими к узкой стенке волновода. Так как вблизи стенок локализуется магнитное поле волны H₁₀, диафрагма возмущает преимущественно это поле и ее эквивалентная проводимость имеет индуктивный характер.

Эквивалентная индуктивность диафрагмы вычисляется так:

. (20.14)

Симметричная (x0 = a/2) индуктивная диафрагма при  = 1 и a  2b вносит параллельную реактивную проводимость в ЛП

. (20.15)

Втонкойемкостной диафрагме (рис. 20.4) металлические пластины примыкают к широкой стенке и возмущают в основном электрическое поле волны H₁₀. Эквивалентная шунтирующая емкость определяется так:

. (20.16)

Симметричная емкостная диафрагма (y0 = b/2 при =1) вносит параллельную реактивную проводимость в ЛП

. (20.17)

Модуль коэффициента отражения Г, вносимого данными L и C диафрагмами, при нормированных проводимостях определяется так:

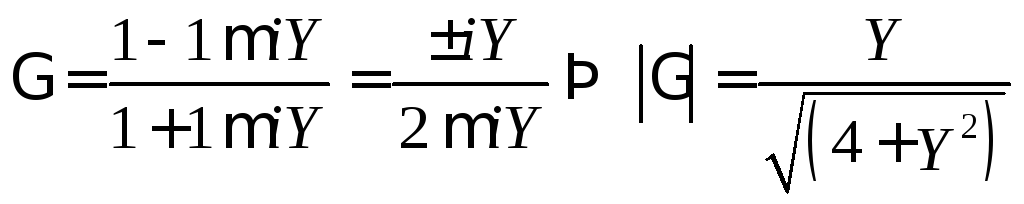. (20.18)

Резонансное окно в прямоугольном волноводе (рис. 20.5) можно рассматривать как наложение двух диафрагм – емкостной и индуктивной. Поэтому эквивалентная схема окна содержит емкостные и индуктивные элементы, включенные в ЛП параллельно. На резонансной частоте ЭМВ проходит через окно без отражений. Резонансные окна используют для разделения вакуумной и невакуумной частей СВЧ-тракта.

Резонансную  окна можно определить из формулы (и– размеры отверстия):

. (20.19)

Индуктивный штырь (L_э) в волноводе расположен параллельно узкой стенке (рис. 20.6). ЭМВ возбуждает в штыре ток, а ток – магнитное поле, запасающее энергию.

. (20.20)

Список рекомендуемой литературы: [2, с. 220–226, 289–292, 324–438; 5, с. 198–210, 274–301; 6, с. 396–410; 9, с. 197–208; 11, с. 267–269, 300–310, 342–350, 379–404; 12, с. 267–276; 13, с. 293–301; 22; 37; 49].