
- •И. В. Богачков Электромагнитные поля и волны
- •Предисловие
- •Тема 1. Введение в теорию эмп
- •Указания к теме
- •Основные сведения
- •Классификация радиоволн
- •Контрольные вопросы и задания
- •Тема 2. Основные уравнения теории эмп
- •Указания к теме
- •Основные сведения
- •Уравнения Максвелла в интегральной форме
- •Уравнения Максвелла в дифференциальной форме
- •Контрольные вопросы и задания
- •Тема 3. Граничные условия для векторов эмп
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 4. Баланс энергии эмп
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 5. Волновые уравнения для векторов эмп
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 6. Плоские эмв в диэлектриках
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 7. Эмп в проводниках
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 8. Эмв в реальных средах. Поляризация эмв
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 9. Эмв на границе раздела двух сред
- •Указания к теме
- •Основные сведения
- •Формулы Френеля
- •Контрольные вопросы и задания
- •Тема 10. Классификация эмп. Особенности квазистационарного эмп
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 11. Электродинамические потенциалы. Основные теоремы и принципы электродинамики
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 12. Излучение эмв
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 13. Плоские эмв в анизотропной среде
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 14. Дифракция эмв
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 15. Условия распространения эмв в направляющих системах
- •Указания к теме
- •Основные сведения
- •Для того чтобы эмв перемещалась в лп, необходимо нахождение и в поперечной плоскости (s).
- •Контрольные вопросы и задания
- •Тема 16. Полые металлические волноводы
- •Указания к теме
- •Основные сведения
- •Эмв в прямоугольном волноводе
- •Волноводы сложных форм сечения
- •Контрольные вопросы и задания
- •Тема 17. Линии передачи т-волны
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 18. Волоконные световоды и другие Линии передачи
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 19. Волновые процессы в нерегулярных линиях
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 20. Элементы линий передачи
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Тема 21. Объемные резонаторы
- •Указания к теме
- •Основные сведения
- •Контрольные вопросы и задания
- •Библиографический список
- •Содержание
Контрольные вопросы и задания
На какие классы можно разделить ЭМП?
Дайте определение основным разновидностям ЭМП.
Укажите основные особенности ЭМП различных классов.
Каковы условия применимости геометрической оптики для анализа ЭМП?
Какие упрощения в анализе ЭМП допустимы для весьма высоких частот?
Когда применимо понятие квазистационарного ЭМП? Какие упрощения в анализе допустимы для квазистационарного ЭМП?
Дайте характеристику поведения магнитного поля в проводнике, двухпроводной и коаксиальной линии.
Дайте определение внутренним и внешним индуктивностям и емкостям. Почему на ВЧ можно учитывать только внешнюю индуктивность?
Какое сходство наблюдается в явлениях электростатики и магнитостатики?
Какие аналогии существуют у статических и стационарных ЭМП?
При каких условиях можно пренебречь волновым характером ЭМП?
Напишите формулы для вычисления погонных емкости и индуктивности для коаксиальной и двухпроводной линий. Есть ли общие множители в формулах для погонной индуктивности и емкости для одной и той же линии?
Какие принципиальные отличия существуют между законами электротехники и электродинамики?
Назовите основные допущения, позволяющие перейти от законов электродинамики к уравнениям электротехники и теории электрических цепей.
Покажите, как первый закон Кирхгофа выводится из системы уравнений Максвелла.
Выведите второй закон Кирхгофа из уравнений электродинамики.
Тема 11. Электродинамические потенциалы. Основные теоремы и принципы электродинамики
Постановка задач в электродинамике. Скалярный и векторный электродинамические потенциалы. Уравнения Даламбера для электродинамических потенциалов. Уравнения Пуассона и Лапласа. Связь электродинамических потенциалов с векторами ЭМП. Решение неоднородных уравнений Даламбера для электродинамических потенциалов. Запаздывающие потенциалы.
Применение электродинамических потенциалов в анализе ЭМП.
Основные теоремы и принципы в теории гармонических полей. Магнитные токи и заряды. Принцип перестановочной двойственности уравнений Максвелла. Теорема единственности для внешней и внутренней задач электродинамики. Принцип эквивалентности. Различные формулировки принципа эквивалентности. Лемма Лоренца. Сопряженная лемма. Теорема взаимности.
Указания к теме
Необходимо выучить определения скалярного и векторного потенциалов, обратить внимание на их связь с векторами и энергией ЭМП, а также на применение в анализе ЭМП; уяснить понятие запаздывающего потенциала.
Пользуясь теоремой Пойнтинга о балансе энергии, можно определить дополнительные условия, наложение которых сообщает решениям уравнений Максвелла физическую определенность (единственность).
Следует выучить формулировки теорем единственности и взаимности, принципов эквивалентности и двойственности, обратить внимание на их место в теории ЭМП.
Основные сведения
При решении задач излучения необходимо решать систему уравнений Максвелла при наличии сторонних источников ЭМП. Введение электродинамических потенциалов позволяет упростить расчет ЭМП излучающих систем. Из условия соленоидальности магнитного поля (2.8) можно записать:
![]()
![]() , (11.1)
, (11.1)
где
введенную функцию
![]() называютвекторным
потенциалом.
называютвекторным
потенциалом.
Подстановка
выражения (11.1) в (2.6) позволяет связать
![]() с
с![]() :
:
![]() или
или
![]() . (11.2)
. (11.2)
Из условия потенциальности электростатического поля
![]()
![]() , (11.3)
, (11.3)
где введенную функцию называют скалярным потенциалом (в случае электростатического поля функция является скалярным электрическим потенциалом) [1, 11].
Векторы
ЭМП можно выразить через
![]() и
:
и
:
![]() ,
,
![]() . (11.4)
. (11.4)
Волновые уравнения для электродинамических потенциалов. Подставляя выражение (11.4) в систему уравнений Максвелла для однородной среды при наличии сторонних источников ЭМП, получаем
![]() . (11.5)
. (11.5)
Удобно
выбрать div так, чтобы в уравнении (11.5) слагаемое в
скобках оказалось бы равным нулю
так, чтобы в уравнении (11.5) слагаемое в
скобках оказалось бы равным нулю
![]() . (11.6)
. (11.6)
Условие (11.6) называют калибровкой Лоренца. В случае равенства нулю правой части (11.6) получается калибровка Кулона [1–3, 11].
С
учетом выражения (11.6) из системы уравнений
Максвелла получаются неоднородные
волновые уравнения
для потенциалов
![]() и
и
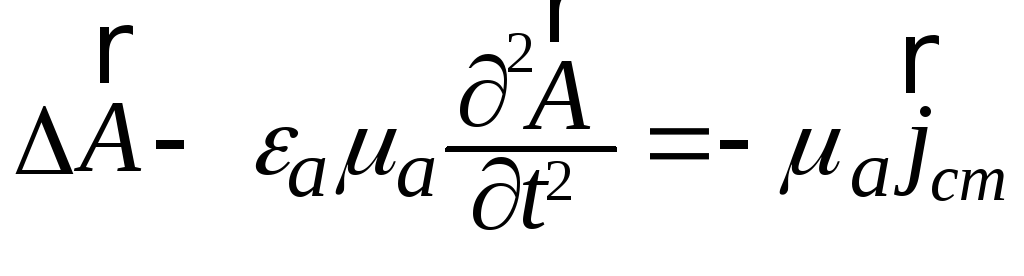 ; (11.7)
; (11.7)
![]() . (11.8)
. (11.8)
После
решения уравнений (11.7) и (11.8) для конкретных
исходных данных векторы
![]() и
и![]() находятся после подстановки
находятся после подстановки![]() и
в (11.4).
и
в (11.4).
В
случае стационарного магнитного поля
![]() можно считатьпотенциальной
энергией токов,
в то же время
связан с
потенциальной
энергией зарядов
в электростатике
[1–3].
можно считатьпотенциальной
энергией токов,
в то же время
связан с
потенциальной
энергией зарядов
в электростатике
[1–3].
При
решении задач излучения с целью уменьшения
числа неизвестных иногда вводят вектор
Герца
![]() [12] (
[12] (![]() ,
,![]() ).
).
![]() ,
,
![]() .
(11.9)
.
(11.9)
В
классической
электродинамике
![]() и
– лишь
вспомогательные
величины, так как для представления ЭМП
необходим переход к
и
– лишь
вспомогательные
величины, так как для представления ЭМП
необходим переход к
![]() и
и![]() .
Вквантовой
электродинамике
.
Вквантовой
электродинамике
![]() и
считаются фундаментальными величинами
[1–3].
и
считаются фундаментальными величинами
[1–3].
Электродинамические потенциалы в безграничном пространстве. Решение уравнений (11.7) и (11.8) в безграничном пространстве упрощается. В пространстве вне точечного источника ст = 0.
Для точечного заряда в ССК и ЦСК решение имеет вид [1–4]
![]() . (11.10)
. (11.10)
При
v
(мгновенное
распространение действия ЭМП) из
уравнений (11.8) получается уравнение
С. Пуассона
[1, 6, 11]
:
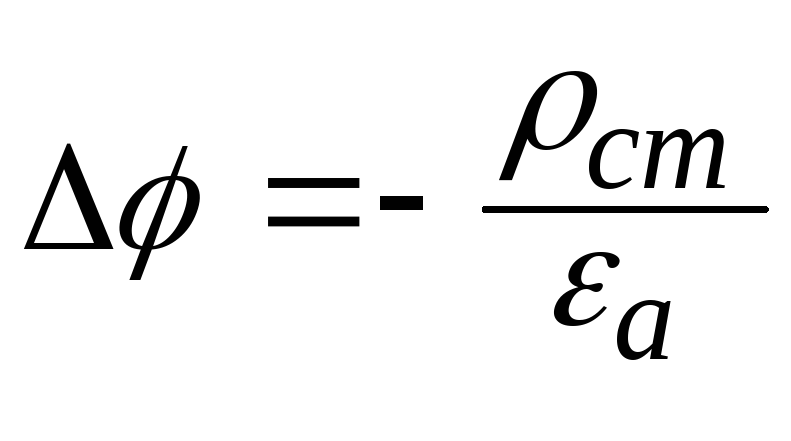 .
.
При
точках незаряженной области (
= 0) уравнение
Пуассона (11.15) переходит в уравнение
П. Лапласа
[6, 11]
:
![]() .
.
Волновое уравнение для векторного потенциала имеет вид [1–3, 11]
![]() (11.11)
(11.11)
Полученные решения (11.10) и (11.11) отражают конечность скорости распространения ЭМП от своих источников. В точке наблюдения значения электродинамических потенциалов (а значит, и векторов ЭМП) определяются значением не в текущий момент времени t, а в предшествующий момент t – r/v. Поэтому решения (11.10) и (11.11) называют запаздывающими потенциалами. Время запаздывания r/v как раз показывает, какое время требуется ЭМВ, чтобы пройти расстояние r с конечной скоростью v [11].
Сравнивая уравнения (11.10) и (11.11) с (5.5) и (5.6), можно сделать вывод, что полученные решения имеют характер сферических волн.
П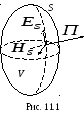 ри
решении задач электродинамики
выделяют внутреннюю
и внешнюю
задачи. Внутренней
называется задача определения ЭМП
внутри области V,
ограниченной замкнутой поверхностью
S
(рис. 11.1), при
заданных на ней граничных условиях для
векторов ЭМП. Примеры внутренней задачи
– определение ЭМП в объемном резонаторе,
определение функции распределения тока
в антенне заданной конструкции.
ри
решении задач электродинамики
выделяют внутреннюю
и внешнюю
задачи. Внутренней
называется задача определения ЭМП
внутри области V,
ограниченной замкнутой поверхностью
S
(рис. 11.1), при
заданных на ней граничных условиях для
векторов ЭМП. Примеры внутренней задачи
– определение ЭМП в объемном резонаторе,
определение функции распределения тока
в антенне заданной конструкции.
Внешняя задача электродинамики заключается в решении уравнений Максвелла для неограниченного пространства вне области V, ограниченной замкнутой поверхностью S , при наличии источников ЭМП. Примеры внешней задачи – определение ЭМП антенны в свободном пространстве при известном распределении тока в антенне, решение задач дифракции.
При
постановке задач электродинамики
необходимо ввести начальные и граничные
условия, сообщающие этим задачам
физическую
определенность
[1]. Векторы ЭМП не могут иметь произвольную
зависимость от координат и времени.
Например, есть ограничения на скорость
убывания амплитуд
![]() и
и![]() .
.
Из
закона сохранения энергии следует [1],
что в пространстве без потерь каждый
из векторов
![]() и
и![]() должен
убывать не медленнее, чем 1/r
. Это
условие называется условием
излучения на бесконечности [1]:
должен
убывать не медленнее, чем 1/r
. Это
условие называется условием
излучения на бесконечности [1]:
![]() =
0 ;
=
0 ;
![]() =
0 . (11.12)
=
0 . (11.12)
Условия(11.12)эквивалентныусловиямизлученияЗоммерфельда
![]() =
0 ;
=
0 ;
![]() =
0 . (11.13)
=
0 . (11.13)
Знак при вторых слагаемых в уравнениях (11.13) определяет, что условия записаны для ЭМВ, которая расходится (удаляется) от источника [1, 5]. При наличии потерь в пространстве, которые учитываются коэффициентом затухания , векторы ЭМП убывают быстрее – пропорционально exp(–r)/r.
Существуют принципы и теоремы электродинамики, которые позволяют существенно упростить решение задач электродинамики и теории антенн.
Теорема
единственности решений уравнений
Максвелла.
Методы
решения уравнений ЭМП могут быть
различными, поэтому необходимо доказать,
что решение, полученное любым методом,
является единственным. В учебных пособиях
[1, 12] приведено доказательство того, что
если при решении уравнений Максвелла
при определенных начальных и граничных
условиях получены значения векторов
ЭМП (![]() и
и![]() ),
то это решение будетединственным.
),
то это решение будетединственным.
Принцип двойственности. Для решения задач теории ЭМП удобно ввести понятия магнитных токов и зарядов. Как отмечалось ранее, эти величины являются фиктивными и вводятся как эквивалент действия электрических токов.
При наличии магнитных источников уравнения Максвелла (2.20)–(2.21) уступают место следующим [1, 13]:
![]() =
=![]() =
=![]() ,
,
![]() , (11.14)
, (11.14)
![]() =
=![]() =
=![]() ,
, ![]() . (11.15)
. (11.15)
где
![]() и
и
![]() –
плотности
сторонних электрического и магнитного
токов соответственно; м
– удельная эквивалентная магнитная
проводимость;
–
плотности
сторонних электрического и магнитного
токов соответственно; м
– удельная эквивалентная магнитная
проводимость;
![]() и
и
![]() –
объемные плотности электрического
и магнитного зарядов.
–
объемные плотности электрического
и магнитного зарядов.
Сопоставляя уравнения Максвелла и выражения (11.14)–(11.15), нетрудно убедиться, что одни полностью переходят в другие при следующей замене:
![]()
![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,![]()
![]() ,a
µa
, э
м,
,a
µa
, э
м,
![]() ,
,
![]()
–
–![]() ,
,![]()
–
–![]() ,
,![]()
–
–![]() ,
,
![]()
–
–![]() ,
,![]()
–
–![]() . (11.16)
. (11.16)
Следует
отметить, что размерности эквивалентных
величин несколько отличаются от обычных
в системе СИ. Оказывается, что
![]() измеряется в вольтах на метр квадратный,
а не в амперах на метр квадратный, как
измеряется в вольтах на метр квадратный,
а не в амперах на метр квадратный, как![]() ,Iм
– в вольтах (размерность U),
Qм
– в веберах (размерность Ф),
м
– в омах на метр (размерность удельного
сопротивления) [1, 7], то есть размерности
прямой и обратной замены отличаются
как сопротивление
и проводимость!
,Iм
– в вольтах (размерность U),
Qм
– в веберах (размерность Ф),
м
– в омах на метр (размерность удельного
сопротивления) [1, 7], то есть размерности
прямой и обратной замены отличаются
как сопротивление
и проводимость!
Таким образом, если найдено ЭМП заданных электрических источников, то достаточно сделать замену (11.16) в готовом решении задачи, и это непосредственно приведет к выражению ЭМП излучения магнитных источников.
О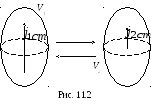 бщий
смыслпринципа
двойственности
состоит в том, что при определенных
условиях электрическое и магнитное
поля «меняются ролями». Кроме того,
симметрия системы уравнений Максвелла
(11.14)–(15.9)
подчеркивает равноправие
электрических и магнитных составляющих
в переменном ЭМП.
бщий
смыслпринципа
двойственности
состоит в том, что при определенных
условиях электрическое и магнитное
поля «меняются ролями». Кроме того,
симметрия системы уравнений Максвелла
(11.14)–(15.9)
подчеркивает равноправие
электрических и магнитных составляющих
в переменном ЭМП.
Лемма Лоренца.
Пусть в некоторой линейной среде имеется
два электрических источника, характеризуемых
функциями плотности стороннего
электрического тока
![]() и
и![]() соответственно (рис. 11.2). После
преобразований
соответственно (рис. 11.2). После
преобразований
![]() .
(11.17)
.
(11.17)
Интегрируя уравнение (11.17) по области V, ограниченной поверхностью S, охватывающей источники ЭМП, с учетом теоремы Остроградского – Гаусса (2.11) получим
![]() .
(11.18)
.
(11.18)
Соотношения (11.17) и (11.18) – это соответственно дифференциальная и интегральная формулировки леммы Лоренца, устанавливающей важные связи между полями двух источников.
В случае свободного пространства в дальней зоне источников (S∞) левая часть соотношения (11.18) стремится к нулю [1, 5, 6], а это приводит к таким соотношениям:
![]() ,
,
![]() . (11.19)
. (11.19)
Принцип взаимности разделенных источников. В случае, когда источники разделены в пространстве, первый источник расположен в области V1, а второй – в области V2 (рис. 11.2), соотношения (11.19) принимают форму
![]() .
(11.20)
.
(11.20)
Интеграл справа можно истолковать как некоторую характеристику взаимодействия ЭМП первого источника с ЭМП второго; аналогичный смысл имеет интеграл слева. Очевидно, что характеристики такого рода равны независимо от типа источников и изотропных сред, в которых они расположены.
Соотношение (11.20) выражает принцип взаимности, подразумевая пространственно разделенные источники и их поля.
Для двух линейных токов из выражения (11.20) следует [1]
![]() ,
(11.21)
,
(11.21)
где
![]() и
и![]() представляют собой э. д. с., наводимые
на каждом из линейных элементов
представляют собой э. д. с., наводимые
на каждом из линейных элементов![]() (I1)
и
(I1)
и
![]() (I2)
полем другого источника.
(I2)
полем другого источника.
Равенство (11.21) можно представить в другой форме:
![]()
![]() ,
(11.22)
,
(11.22)
где
![]() и
и![]() имеют смыслвзаимных
сопротивлений.
имеют смыслвзаимных
сопротивлений.
Принцип взаимности проявляется в том, что э. д. с., наводимая на первом элементе заданным током второго, оказывается такой же, как и э. д. с. на втором элементе при равном токе первого [1].
Э. д. с., наводимая в приемной антенне в зависимости от ее ориентации, изменяется по тому же закону, что и ЭМП в дальней зоне, создаваемое этой антенной в режиме передачи. То есть направленность действия антенны при приеме и передаче одинакова. В теории антенн принцип взаимности позволяет использовать характеристику направленности передающей антенны (ДН) при использовании этой антенны в качестве приемной, а также использовать измеренную характеристику ДН приемной антенны и в режиме передачи.
Среды, устройства и системы, в которых выполняется принцип взаимности, называют взаимными [1].
Список рекомендуемой литературы: [1, гл. 11, 15, с. 55–59, 83–90; 2, с. 75–78, 123–126, 132–139, 150–152; 3, гл. 11, с. 51–55; 4, с. 47–50; 5, с. 21–24, 52–55, 223–239; 6, с. 128–138, 172, 205–212; 7, с. 63–67, 244–279; 8, с. 18–25, 57–61; 9, с. 60–61, 143–154, 157–159; 10, с. 68–70; 11, с. 61–75, 121–125; 12, с. 63–65, 94–98, 106–132; 13, с. 134–140, 150–155, 165–168, 238–241; 32, с. 13–17; 34, с. 5–10; 35, с. 11–13; 36, с. 9–12].
