Эмв в прямоугольном волноводе

Поверхность прямоугольного волновода (рис. 16.2) S, образуется плоскостями x = 0, y = 0, x = a, y = b. Обычно широкая стенка а в 2–2,5 раза длиннее стенки b.

После вычислений, подробно рассмотренных в рекомендуемой литературе, получаем решения для продольных компонент. Решение для Н-волн и Е-волн имеют вид

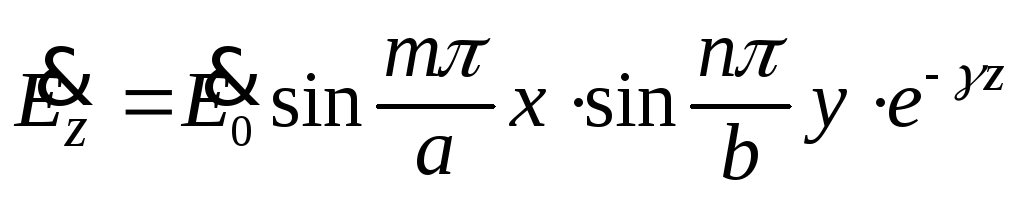, , (16.7)

где ,– комплексные амплитуды генератора [1–3].

Выражения (16.7) соответствуют бесконечному множеству решений, отличающихся натуральными числами m и n. Физически m означает количество вариаций (полуволн) поля вдоль оси x, а n – количество вариаций вдоль оси y. Таким образом, в прямоугольном волноводе может существовать бесконечное множество волн, обозначаемых Н_mn (например, Н₁₀ , Н₂₁) или Е_mn. Разница между E- и H-волнами заключается в том, что Е-волны с «0»-индексом существовать не могут, поскольку в (16.7) в этом случае продольная составляющая Е_z будет равна нулю.

Типы волн Н_mn , называемые также модами, имеют свои критические длины волн и частоты, которые вычисляются из формул

,

. (16.8)

Е-волны имеют такие же критические длины волн и частоты, что и H-волны. E- и H-волны с одинаковыми индексами имеют одинаковые критические частоты и считаются вырожденными [1–3].

Анализ (16.8) показывает (см. также рис. 16.3), что низшими критическими частотами будут обладать магнитные волны вида Н_m0

(при a = 2b) и т. д. (16.9)

Из (16.9) следует, что диапазон частот одномодового режима

. (16.10)

Таким образом, основным типом волн в прямоугольном волноводе является мода Н₁₀ , имеющая наименьшую критическую частоту.

Если , то ЭМВне распространяется.

Из (16.3)–(16.5) и рис. 16.3 следует, что распространяющаяся в прямоугольном волноводе ЭМВ имеет существенную дисперсию, что может привести к значительным искажениям передаваемого сигнала.

Если на некоторой частоте может существовать несколько типов волн (многомодовый режим передачи), то искажения сигнала усиливаются. Каждый тип волн имеет свои харак­теристики распространения, поэтому ЭМВ, распространяемые модой определенного типа, проходят волноводную линию с различными характеристиками распространения. Кроме того, на нерегулярностях волноводных трак­тах возможно взаимное преобразование различных мод. В результате получаются различные фазовые набеги ЭМВ, которые при сложении этих волн на приемном конце приводят к искажениям информации.

На практике обычно используют одномодовый режим (Н₁₀).

Для нахождения всех типов волн, которые могут существовать на заданной частоте, формулу (5.9) необходимо свести к каноническому уравнению эллипса (А и В – полуоси эллипса). После построения эллипса на бумаге в клетку (рис. 16.4), выбираем натуральные значения m и n, которые попали внутрь эллипса.

Потери в волноводе. В случае односвязных волноводов общие потери в волноводе определяются в основном потерями в проводнике. Идеально ровной поверхность волновода выполнить невозможно, поэтому неровность поверхности оценивают коэффициентом шероховатости k_ш. В диапазоне сантиметровых волн k_ш = 1,1–1,5.

Коэффициент затухания волны Н₁₀ :

. (16.11)

где  определяется по формулам (5.17) и (7.1), k – по (16.1).

На рис. 16.5 приведены графики частотной зависимости коэффициента затухания для различных мод прямоугольного волновода. Анализ (16.11) показывает, что частотная характеристика затухания мод типа Н_m0 имеет пологий минимум в районе (2–3)f_кр , с ростом частоты затухание увеличивается пропорционально из-за скин-эффекта, а с понижением частоты от2f_кр до f_кр затухание возрастает пропорционально из-за умень-шения групповой скорости [1–3, 7].

Отсюда следует, чтонижнюю часть одномодового диапазона частот не следует использовать из-за значительного затухания.

Таким образом, полоса рабочих частот прямоугольного волновода

. (16.12)

Например, для волновода из меди 2310 (мм) диапазон частот одномодового режима составит от 6,5 ГГц до 13,0 ГГц, а рабочий диапазон – от 8,2 ГГц до 12,9 ГГц. На частоте 17 ГГц (полуоси эллипса А = 2,61 и В = 1,13; рис. 16.4) будут распространяться моды Н₁₀, Н₂₀, Н₁₁ и E₁₁ (Н₀₁ не учитываем). На частоте 10 ГГц при k_ш = 1,4 коэффициент затухания составит 0,018 1/м, при длине волновода 20 м затухание составит 3 дБ.

Предельно передаваемая мощность в прямоугольном волноводе. Предельно допустимая мощность в волноводе определяется главным образом пробивной напряженностью заполняющего диэлектрика. Для сухого воздуха при нормальном давлении E_проб = 30 кВ/см. Для повышения допустимой напряженности используют сухой разреженный воздух. У волны основного типа предельная мощность определяется величиной

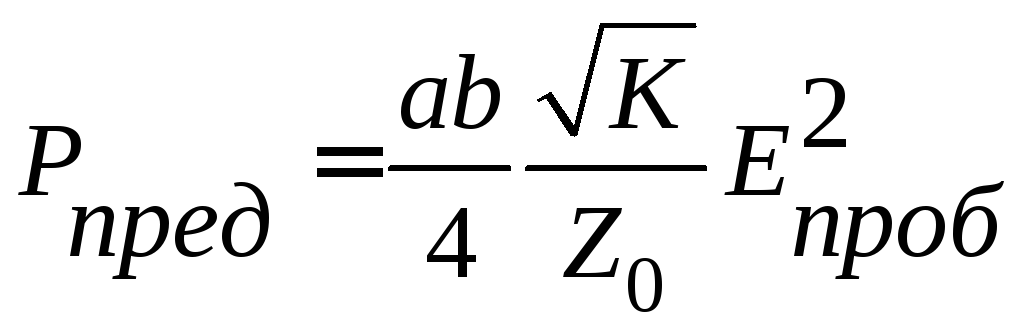. (16.13)

ЭМВ в круглом волноводе

Д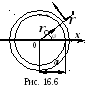ля анализа ЭМП в круглом волноводе удобно использовать ЦСК (рис. 16.6). После вычислений, подробно рассмотренных в рекомендуемой литературе, получаем решения для продольных компонент. Решение дляЕ-волн

; . (16.14)

где _nm – m-й корень функции Бесселя n-порядка.

. (16.15)

Решение для Н-волн

; , (16.16)

где _nm – m-й корень первой производной функции Бесселя n-порядка.

. (16.17)

Физически n показывает периодичность ЭМП (число полуволн) по φ, а m – по r [2]. Для вычисления _nm и _nm используют таблицы и ряды. Из таблиц функций Бесселя получаем наименьшие значения _nm и _nm:

μ₁₁ = 1,8412 – Н₁₁ ; γ₀₁ = 2,4038 – Е₀₁ ; μ₂₁ = 3,0542 – Н₂₁;

μ₀₁, γ₁₁ = 3,8317 – Н₀₁, Е₁₁ и т. д.

Таким образом, полоса частот одномодового режима в круглом волноводе находится между критическими частотами волн H₁₁ и E₀₁.

, . (16.18)

Волна H₁₁ является основным типом в круглом волноводе. Структура ЭМП этой моды имеет ту же структуру, что и мода H₁₀ в прямоугольном волноводе при соответствующей деформации волновода.

К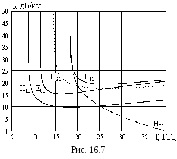роме ЭМВ основного типа, на практике используют и другие моды.

Типы волн Н₀₁ и E₀₁ имеют структуру ЭМП, симметричную относительно оси волновода, которая не изменяется при вращении. Это свойство используется во вращающихся сочленениях [2].

Затухание моды H₁₁ имеет частотную зависимость, аналогичную моде H₁₀ в прямоугольном волноводе (рис. 16.7).

Отсюда следует, что нижнюю часть одномодового диапазона частот не следует использовать из-за значительного затухания.

Таким образом, полоса рабочих частот круглого волновода

. (16.19)

Моды вида Н_0m имеют очень малое затухание, которое уменьшается с ростом частоты (рис. 16.7). Волна Н₀₁, имеющая минимальное затухание, используется для передачи ЭМВ на дальние расстояния [2, 27].

Для нахождения всех типов волн, которые могут существовать на заданной частоте, в (16.15) и (16.17) заменяем γ_nm и μ_nm на X, после вычисления X в таблице функций Бесселя находим все значения γ_nm и μ_nm, которые меньше X.

Затухание Н-волн оценивается следующей формулой:

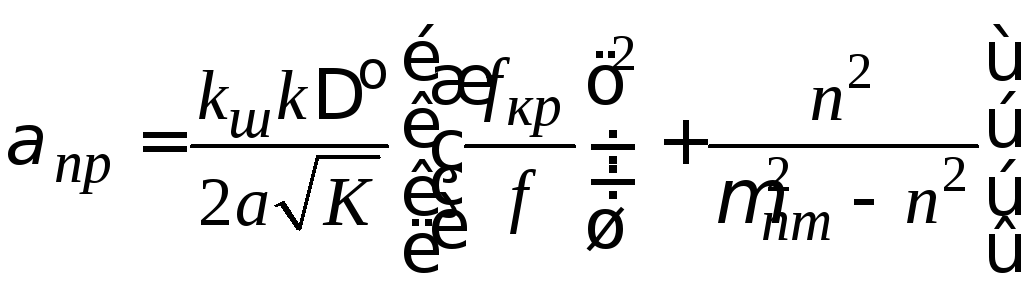. (16.20)

На рис. 16.7 приведены графики частотной зависимости коэффициента затухания для различных мод круглого волновода.

Например, для медного волновода радиусом 10 мм диапазон частот одномодового режима составит от 8,8 ГГц до 11,5 ГГц, а рабочий диапазон – от 10,0 ГГц до 11,4 ГГц. На частоте 12 ГГц (X = 2,51 > μ₁₁ и γ₀₁) будут распространяться моды Н₁₁ и E₀₁ . На частоте 10 ГГц при k_ш = 1,4 коэффициент затухания для Н₁₁ составит 0,023 1/м. Коэффициенты затухания мод Н₁₁ и Н₀₁ равны на частоте 31 ГГц (0,008 1/м), но на f = 50 ГГц (Н₀₁) = 0,003 1/м, что примерно в 3 раза меньше, чем  (Н₁₁).

Предельная мощность моды Н₁₁ рассчитывается по формуле [2, 21]

. (16.21)