Контрольные вопросы и задания

1. Дайте определение проводника с точки зрения теории ЭМП.

2. Всегда ли металлы являются проводниками?

3. Дайте объяснение скин-эффекту в проводниках.

4. Какова скорость движения электронов в проводнике при постоянном токе?

5. Укажите основные особенности частотной характеристики и дайте характеристику поведения импеданса проводника.

6. Дайте характеристику граничным условиям для идеального проводника.

7. Каковы критерии выбора металла для экранирования пространства от ЭМП?

8. Каковы критерии выбора металла для локализации ЭМП с минимальными потерями?

9. Почему групповую скорость ЭМВ в металле можно принять равной нулю?

10. Выведите формулу сопротивления проводника с квадратной формой сечения для случая сильного скин-эффекта. Сравните с результатом для проводника с круглой формой поперечного сечения.

11. Можно ли использовать микроволновую печь для нагрева металлов?

12. Дайте сравнительную характеристику распространения ЭМВ в идеальных диэлектриках, диэлектриках с потерями и проводниках.

Тема 8. Эмв в реальных средах. Поляризация эмв

Общая схема анализа ЭМП в реальной среде.

Поляризация волн. Линейно поляризованные волны. Волны с круговой и эллиптической поляризациями. Связь линейной и круговой поляризации. Понятие о поляризационной селекции сигналов. Кросс-поляризация.

Указания к теме

Для решения практических задач чрезвычайно важно хорошо представлять особенности распространения ЭМВ в различных средах, уметь правильно классифицировать среды, рассчитывать основные характеристики и параметры ЭМВ в них. Среди различных факторов, влияющих на скорость распространения волны и ее затухание, следует обратить внимание на их зависимость от частоты.

Необходимо выучить определения поляризации ЭМВ и ее разновидностей, научиться правильно определять поляризацию ЭМВ.

Основные сведения

Общая схема анализа ЭМВ в реальных средах. ЭМП в виде плоских ЭМВ в заданной среде удобно анализировать по следующей схеме.

1. Находим tg по формуле (2.15).

Классифицируем среду (диэлектрик, проводник, полупроводник) в зависимости от значения tg по формулам (2.16).

2. Находим  и  по формулам для соответствующего вида среды:

общий случай и полупроводник – (5.13) и (5.14);

диэлектрик – (6.1) и (6.2);

проводник – (7.1).

3. Находим характеристики ЭМВ (групповая и фазовая скорость, длина волны, затухание, волновое сопротивление и т. п.) и записываем формулу плоской ЭМВ (5.11) или (5.12) для соответствующей среды:

полупроводник – тема 5, формулы (5.15)–(5.20), (5.22)–(5.24);

диэлектрик – тема 6, формулы (6.3)–(6.5);

проводник – тема 7, формулы (7.2)–(7.4).

Поляризацию ЭМВ определяют по ориентации вектора .

Плоскостью поляризации называют плоскость, проходящую через направление распространения и вектор . Считаем, что осьx ориентирована горизонтально, а ось y – вертикально. Достаточно рассмотреть поведение , так как связь сизвестна:.

Запишем мгновенное значение в ДСК:

. (8.1)

Л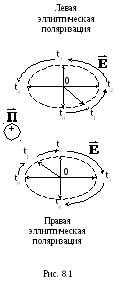инейно поляризованной называют волну, у которой направление вектора (а значит, и)не изменяется с течением времени. Если в формуле (8.1) B = 0, то имеет толькогоризонтальную составляющую, в этом случае ЭМВ имеет горизонтальную поляризацию. Если в формуле (8.1) A = 0, то имеет тольковерти­каль­ную составляющую, в этом случае ЭМВ поляризована вертикально.

Поляризация называется эллиптической, если проекция вектора на плоскость, перпендикулярную направлению распространения, пред­­ставляет собойэллипс (рис. 8.1).

Если фазовый сдвиг между компонентами составляет  = /2+n, то конец вектора с течением времени опишетэллипс.

Пусть _x = 0, тогда E_x  , аE_y  . В этом случае

представляет собой эллипс с полуосями A и B.

Эллиптическую поляризацию можно получить сложением двух ЭМВ ортогональных линейных поляризаций.

Круговая поляризация (проекция на плоскость, перпендикулярную направлению распространения, естькруг) – частный случай эллиптической, когда полуоси эллипса равны между собой. При этом амплитуда ЭМВ остается постоянной ().Угол  между мгновенным значением и осьюx определяется соотношением [1, 11]

. (8.2)

Из соотношения (8.2) следует, что в каждой фиксированной точке наблюдения в плоскости z=const угол  линейно возрастает со скоростью  с течением времени, изменяясь на 2 за время одного периода T (T = 2).

Направление вращения определяется поведением проекции данного вектора на плоскостьx0y (z = const). Если смотреть в направлении распространения ЭМВ, и вектор вращаетсяпо часовой стрелке (рис. 8.1, 8.3), то такая поляризация называется правовинтовой. Если вращение происходит против часовой стрелки (рис. 8.1, 8.2), то эта поляризация – левовинтовая [1, 2].

К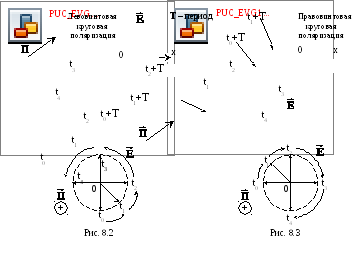руговая поляризация может быть получена суммированием двух ЭМВ ортогональных линейных поляризаций с равными амплитудами. Верно и обратное свойство: эллиптически или линейно поляризованную ЭМВ можно получить суммированием двух волн с круговой поляризацией и противоположными направлениями вращения (рис. 8.4).

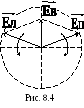Разделение ЭМВ по поляризации позволяет выполнятьполяризационную селекцию сигналов. В каждом конкретном случае выбирается основная поляризация. В этом случае поляризация, ортогональная основной, будет паразитной. В идеале ЭМВ паразитная поляризация не должна приниматься антенной, настроенной на основной вид поляризации. Однако реально полностью подавить паразитную поляризацию не удается. На неоднородностях на трассе распространения ЭМВ и линии передачи может происходить изменение характеристик поляризации, что приводит к кросс-поляризации.

Например, в радиолокации для уменьшения мешающих отражений от водяных паров в атмосфере (гидрометеоров) используют разделение по поляризации. Если правовинтовая поляризация выбрана как основная, то в конструкцию антенны включают поляризационную систему, которая с минимальным ослаблением пропускает ЭМВ основной поляризации, но существенно ослабляет паразитную (левовинтовую) поляризацию.

Список рекомендуемой литературы: [1, гл. 10, с. 52–55; 2, с. 60–62; 3, гл. 10, с. 48–51; 4, с. 44–47; 5, с. 30–32; 6, с. 146–153; 7, с. 86–90; 9, с. 134–137; 10, с. 134–138; 11, с. 139–143; 12, с. 155–162; 13, с. 76–180].