Контрольные вопросы и задания

1. Дайте определение диэлектрика с точки зрения теории ЭМП.

2. Какие разновидности диэлектриков можно выделить в зависимости от молекулярной структуры вещества и ЭМ свойств?

3. Дайте определение поляризуемости и намагниченности вещества.

4. На какие группы делятся вещества в зависимости от их магнитных свойств?

5. Укажите физические основы микроволнового нагрева.

6. Как определяется оптимальная частота при диэлектрическом нагреве?

7. Сравните характеристики распространения ЭМВ в диэлектриках с потерями, без потерь и в проводящих средах.

Тема 7. Эмп в проводниках

Коэффициенты фазы и ослабления при большом tg. Длина волны. Фазовая и групповая скорость. Волновое сопротивление. Проникновение ЭМП в проводник, поверхностный эффект, глубина проникновения.

Сопротивление цилиндрического провода. Случай слабо и сильно выраженного поверхностного эффекта. Частотная характеристика поведения импеданса проводника. Понятие поверхностного импеданса.

Приближённые граничные условия Леонтовича, условия их применимости. Расчет потерь энергии в проводниках. Понятие экрана для ЭМП. Выбор материала проводников для экранирования и локализации ЭМП.

Указания к теме

Для решения практических задач необходимо хорошо представлять особенности распространения ЭМВ в проводящих средах, уметь рассчитывать основные характеристики волнового процесса в этих средах: скорость распространения, длину волны, коэффициенты затухания и фазы, волновое сопротивление и другие. Следует обратить особое внимание на зависимость этих параметров от частоты.

Необходимо изучить явление скин-эффекта в проводниках, законы распределения векторов электрического и магнитного поля по сечению проводника, а также поведение частотной характеристики активного и реактивного сопротивлений проводников. Следует запомнить формулировки граничных условий для проводников, критерии выбора материалов для экранирования и локализации ЭМП.

Основные сведения

Если , то в формулах (5.13) и (5.14) можно пренебречь единицей, что в итоге дает:

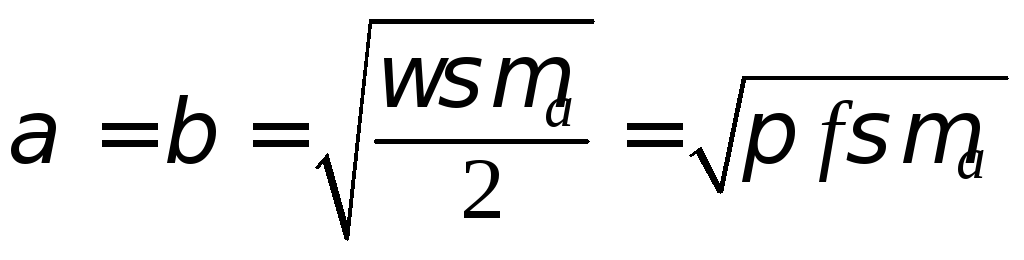. (7.1)

Анализ показывает, что при ВЧ и выше коэффициент затухания в проводнике достигает значительных величин ( пропорционален ). Соответственно глубина проникновения ЭМП в проводник () составляет мкм (УВЧ) и мм (на ВЧ). Таким образом, ЭМП в проводник не проникает, концентрируясь в тонком поверхностном слое, называемом скин-слоем. Данное явление называют скин-эффектом (англ. skin – оболочка, кожа).

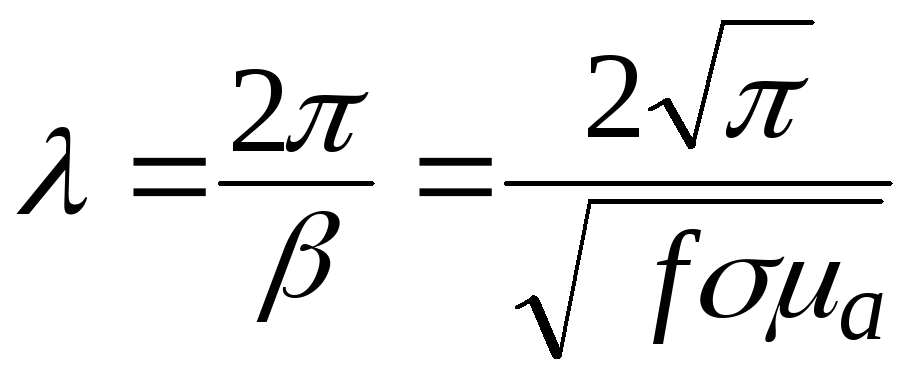. (7.2)

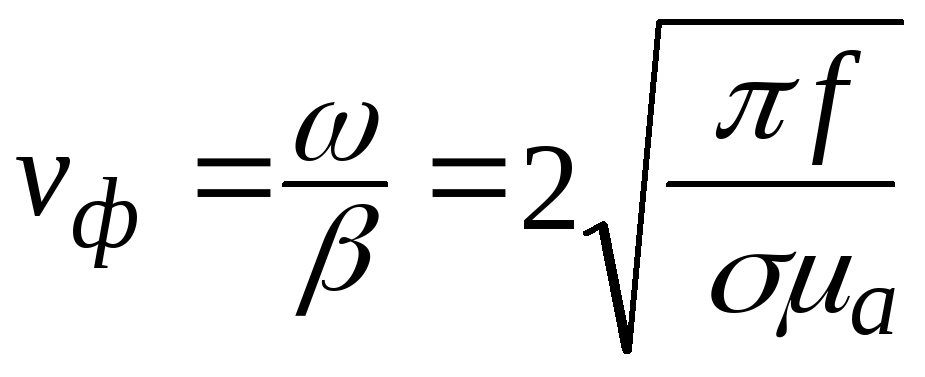. (7.3)

При прохождении в проводнике расстояния, равного , ЭМВ испытывает очень большое затухание . Поэтому пространственная периодичность поля ЭМВ в проводнике отсутствует, иv_гр  0.

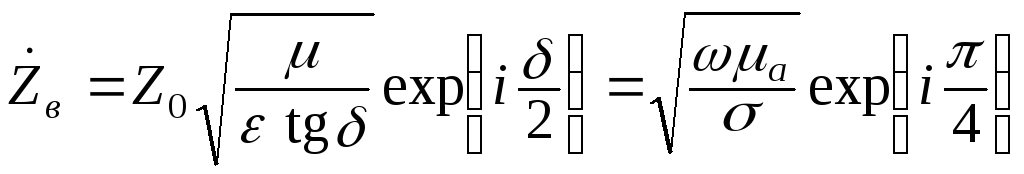
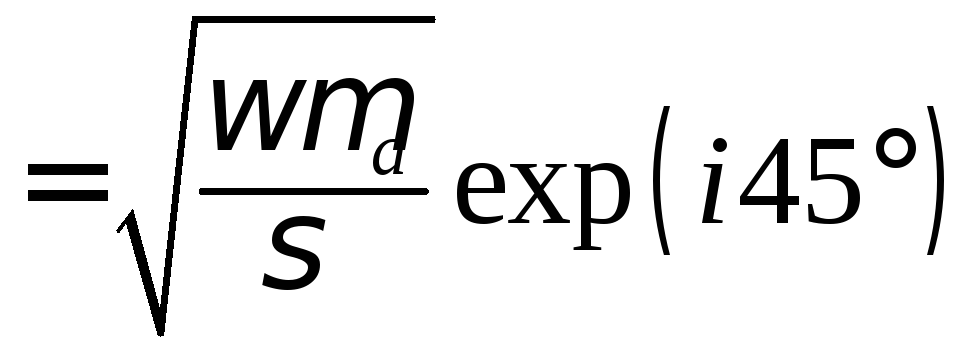. (7.4)

Волновое сопротивление проводника имеет примерно одинаковые по модулю активную и реактивную части, поскольку при tg > 10 для проводников  > 84. Комплексное волновое сопротивление проводника имеет активно-индуктив­ный характер, поскольку отстает по фазе отна 45.

Например, для меди при частоте ЭМП 1 МГц (₀ = 300 м) получаем  =  = 1,5  10⁴ (1/м), v_ф = 420 (м/с),  = 4,2  10^–4 (м),  = 67 (мкм), v_гр = 0, Z_c = 3,7  10^–4  exp (i/4) (Ом) [1].

Сопротивление проводников на высоких частотах. В случае постоянного тока сопротивление проводника цилиндрической формы можно описать формулой (a – радиус проводника):

. (7.5)

На ВЧ и выше (при сильном скин-эффекте) ЭМП концентрируется в тонком поверхностном слое (рис. 7.1), что приводит к уменьшению площади поперечного сечения проводника (S_экв = S₀ – S_вн), по которой протекает ток

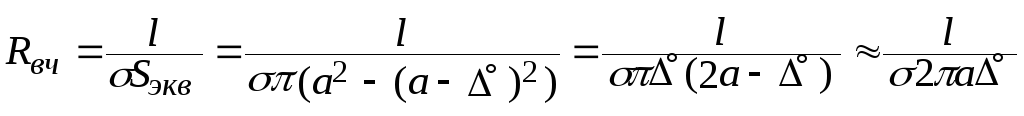. (7.6)

Обобщая выражение (7.6) для проводника с произвольной формой сечения, при сильном скин-эффекте получим

, (7.7)

где p_r – периметр поперечного сечения проводника.

Из отношения (7.6) к (7.5) можно найти относительное увеличение активного сопротивления проводника с ростом частоты:

. (7.8)

При расчетах на ВЧ и выше (f  f1) используют формулу (7.8) (R_вч и X_вч), а при f < f1 считают, что Z₁ = R₀. Значение f1 соответствует частоте, на которой  = 0,5a.

. (7.9)

Распределение магнитного поля по проводнику H_ имеет аналогичный характер, поэтому иногда говорят и о магнитном скин-эффекте.

Для металлического листового проводника (размеры проводника много больше его толщины d) для сильного скин-эффекта получаем

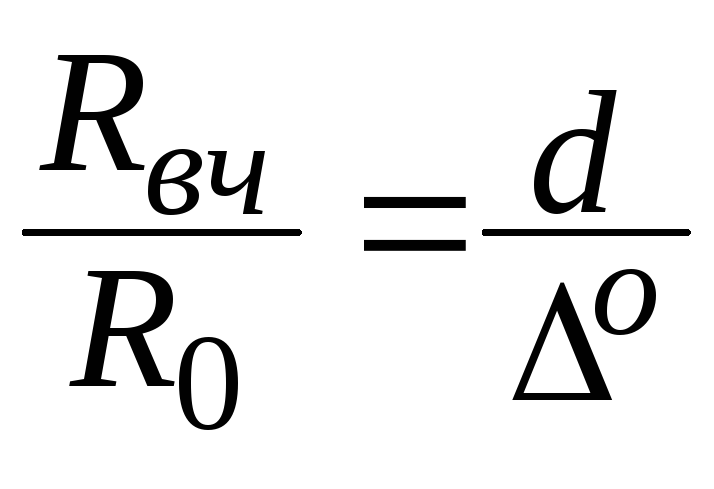. (7.10)

Таким образом, напряженность ЭМП и плотность тока в цилиндрическом проводнике уменьшаются с увеличением расстояния от поверхности медленнее, чем при плоской граничной поверхности, поскольку ЭМВ распространяются к оси проводника по радиусам навстречу друг другу [1–4]. В целом для ОВЧ и выше можно считать, что ЭМП в проводник практически не проникает, что позволяет упростить граничные условия.

Граничные условия для идеального проводника. Данные граничные условия получаются из общих граничных условий, при этом считается, что ЭМП не проникает во вторую среду – идеальный проводник (= 0,= 0).

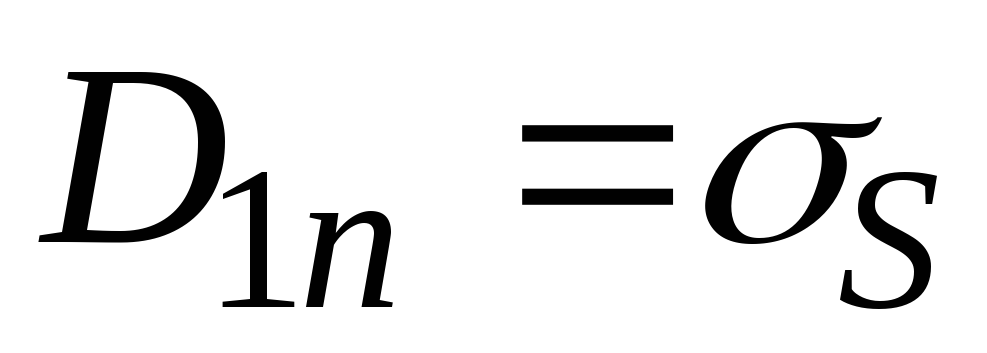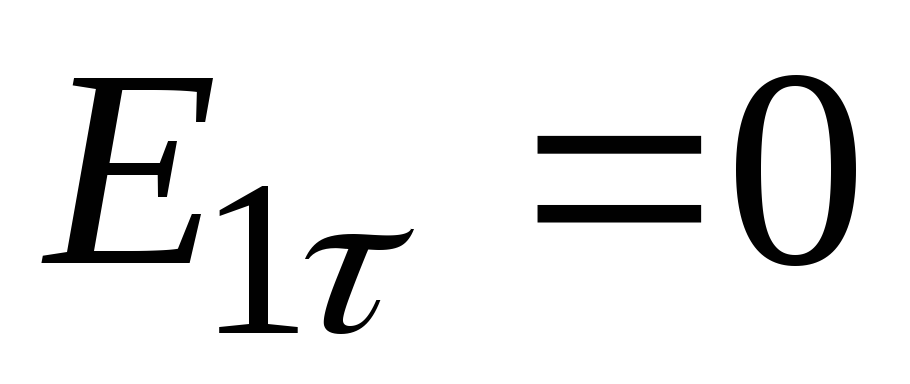, (условиеП. Дирихле), ,. (7.11)

Последнюю формулу (7.11) чаще записывают в виде

(условие К. Неймана). (7.12)

Из формулы (7.12) следует, что на границе с проводником имеет экстремум (максимум).

При анализе ЭМП на границе важную роль играет поверхностный импеданс (векторы напряженностей ЭМП параллельны границе раздела):

; . (7.13)

Поверхностный импеданс на границе раздела с оптически очень плотной средой равен ее Z_в (приближенное граничное условие М. Леонтовича) [2]. Из граничных условий (7.11) следует, что наводит поверхностные токи.

Выбор материала проводников для экранирования и локализации ЭМП. Так как ЭМВ быстро затухает в проводнике, металлические проводники можно использовать для экранирования какой-либо области пространства от воздействия ЭМП или, наоборот, для локализации ЭМП в определенной области пространства (например, в объемном резонаторе). Так как толщина скин-слоя для металла из-за больших значений  составляет доли миллиметра даже для ВЧ, экраном небольшой толщины можно существенно ослабить действие ЭМП.

Например, медный экран толщиной 1 мм ослабляет ЭМВ частотой 5 кГц в 2,9 раза (на 9,2 дБ), а ЭМВ частотой 1 МГц – в 3,110⁶ раз (на 130 дБ). Пользуясь формулами (5.15) или (5.16), можно при заданной частоте рассчитать ослабление ЭМП, создаваемое экраном определенной толщины, или, наоборот, вычислить толщину экрана из выбранного материала при заданном ослаблении ЭМП.

Следует отметить, что на ОВЧ и выше экранирующий эффект определяется в основном отражением ЭМВ от экрана, а не ослаблением.

Проанализируем с помощью формул (5.16) и (7.1), какими свойствами должен обладать материал экрана для получения максимального ослабления ЭМП. При заданной частоте и толщине экрана, получаем пропорциональность

~ . (7.14)

Таким образом, для получения максимального ослабления желательно выбирать магнитный материал с высокой проводимостью.

Следует учесть, что большие значения  у трансформаторных сталей достигаются только на НЧ, а с ростом частоты значение (f) резко уменьшается, и для экранирования ВЧ ЭМП эти материалы неэффективны.

Проанализируем, при каких параметрах потери в проводниках будут минимальны. Токи проводимости в проводнике наводятся .

В случае сильного скин-эффекта в проводнике плотность потока мощ­нос­ти тепловых потерь с учетом условия Леонтовича описывается формулой [1, 2]

. (7.15)

Для листового проводника площадью S с помощью формулы (7.15) можно рассчитать мощность тепловых потерь, наводимых ЭМП в металле [1, 2]

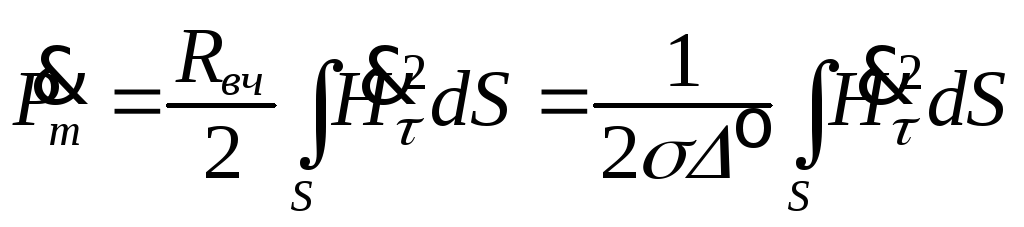. (7.16)

Данная формула не учитывает краевых эффектов. Считается, что площадка S находится в средней части протяженного металлического листа [1, 2].

Из выражения (7.16) получим зависимость мощности потерь от параметров металлического проводника

~ . (7.17)

Из формулы (7.17) следует, что для минимальных потерь в металлическом проводнике, который находится под воздействием ЭМП, следует использовать немагнитный материал с высокой проводимостью.

Список рекомендуемой литературы: [1, гл. 9, с. 45–51; 2, с. 57–59, 105–113; 3, гл. 9, с. 41–48; 4, с. 39–44; 5, с. 38–41; 6, с. 145–146, 185–189; 7, с. 109–114; 9, с. 65–68, 172–176, 283–284; 10, с. 65–68; 11, с. 138–139, 163–174; 12, с. 195–204, 217–219; 13, с. 176–177, 211–222].