Цифровая схемотехника

(AмD)(AмB)(BмC)ъ(AмBD)(BмC)ъ ъABмACмBDмBCDъABмACмBD

Каждая полученная в результате конъюнкция соответствует ТДНФ, все они являются МДНФ. Записываем получившиеся МДНФ, не забывая дописать существенную импликанту:

AB: г(й,ц,у,к)ъфывмфвкмуа

AC: г(й,ц,у,к)ъфывмцвкмуа

BD: г(й,ц,у,к)ъфвкмфыамуа

Получившиеся МДНФ могут отличаться значениями на запрещенных наборах, например, функция, записанная по варианту AB, на наборе 1101 равна 0, а по варианту AC – 1. Но на всех разрешенных наборах все записи функций совпадают.

3.1.5. Упражнения

1. Минимизировать функцию методом Квайна:

г(й,ц,у,к)ър(0,1,4,5,6,8,9,10,14)

2. Минимизировать функцию методом Квайна-Мак-Класки:

г(й,ц,у,к,е5)ър(1,2,5,6,7,8,9,10,11,18,22,24,25,26,27)

3. Минимизировать функцию методом Квайна-Нельсона:

г(й,ц,у,к)ър(2,3,5,6,7,8,9,10,12,13,14)

4. Минимизировать частично заданную функцию методом Квайна:

г(й,ц,у,к)ър(0,4,10,11,13,14,15)ь(1,2,3,5,7)

3.2. Метод карт Карно

3.2.1. Построение карт Карно

При минимизации функций алгебры логики в первую очередь используется правило склеивания (1.25). Карты Карно позволяют избавиться от склеиваний в аналитическом виде, а проводить их прямо по карте, что дает возможность проще и быстрее минимизировать функции.

Склеить можно две конъюнкции, которые отличаются только знаком отрицания у одного аргумента, например, йцук и йцуа. Будем называть такие конъюнкции соседними. Каждая конъюнкция высшего ранга соответствует определенному набору аргументов. Два набора, отличающиеся только в одном разряде, будем называть соседними наборами, например, 1111 и 1110.

Карта Карно представляет собой совокупность клеток, каждая из которых соответствует своему набору аргументов, поэтому число кле-

40

Комбинационные схемы

ток в карте равно 2n , где n – количество аргументов функции. Координаты клеток определяют тот набор, которому соответствует клетка. В клетки карты ставится значение функции: 1, 0 или * (для запрещенных наборов). Нулевое значение обычно не пишут, оставляя клетку пустой. Клетки в карте расположены таким образом, чтобы соседние клетки соответствовали соседним наборам аргументов. Это позволяет проводить склеивания прямо по карте с помощью специальных обозначений.

Карту Карно для функции 2-х аргументов можно нарисовать тремя способами: в виде квадрата (рис. 3.2, а), вытянув клетки в строку (рис. 3.2, в) или в столбец (рис. 3.2, б). Если карта нарисована в виде квадрата, то столбцы можно обозначить аргументом й, а строки – аргументом ц. Тогда левая верхняя клетка карты будет соответствовать набору 00, левая нижняя – набору 01 и т.д. Если четыре клетки карты вытянуты в строку или в столбец, то их приходится обозначать двумя аргументами – йц. Чтобы нанести функцию на карту (например, г(й,ц)ър(1,2)ь(0) ), проставляем в клетки соответствующие значения.

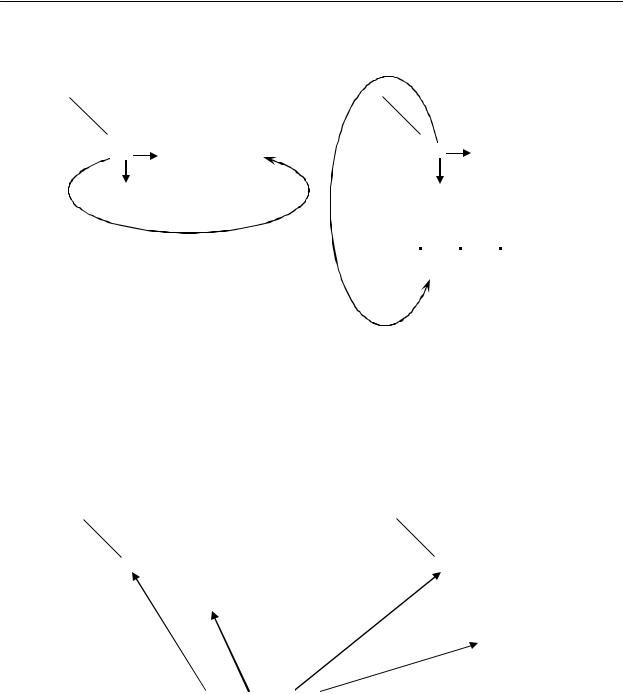
У каждого набора аргументов – два соседних набора, поэтому и в карте Карно у каждой клетки должно быть две соседних клетки. Когда клетки расположены в виде квадрата, это получается автоматически, например, у клетки, соответствующей набору 00, справа будет клетка набора 10, а снизу – 01. Но если клетки вытянуты в строку или в столбец, то обозначать их нужно не по порядку, а так называемым кодом Грея, где каждый следующий код отличается от предыдущего в одном разряде. Тогда у каждой клетки рядом будут по две клетки с соседними наборами. Чтобы у крайних клеток рядом стояли две соседние, нужно карту свернуть в цилиндр по горизонтали (рис. 3.2, в) или по вертикали (рис. 3.2, б). Тогда рядом с клеткой 00 будут стоять клетки 01 и 10 (показаны стрелками).

б)

Рис. 3.2

41

Цифровая схемотехника

В карте Карно для функции 3-х аргументов должно быть 8 клеток, которые можно нарисовать двумя способами (рис. 3.2).

Рис. 3.3

У каждого набора аргументов – три соседних набора, поэтому и в карте Карно у каждой клетки должно быть три соседних клетки. Для этого обозначаем столбцы (рис. 3.3, а) или строки (рис. 3.3, б) кодом Грея. Чтобы у крайних клеток рядом стояли три соседние, нужно карту свернуть в цилиндр по горизонтали (рис. 3.3, а) или по вертикали (рис. 3.3, б). При этом номера наборов идут не по порядку (рис. 3.4).

Рис. 3.4

В карте Карно для функции 4-х аргументов должно быть 16 клеток, которые изображают в виде квадрата (поэтому называются квадратные карты Карно). Строки и столбцы обозначают кодом Грея, а чтобы крайние клетки стояли рядом, нужно эту карту склеить в цилиндр по горизонтали и по вертикали (рис. 3.5). Номера наборов будут идти не по порядку, но зато у каждой клетки рядом будут по 4 соседних клетки. Например, у клетки номер 8 (соответствует набору 1000) соседние клетки 12 (1100), 9 (1001), 1(0000) и 10 (1010).

42

Комбинационные схемы

Рис. 3.5

Чтобы нанести функцию на карту, ставим в соответствующие клетки 1 и *, например, для функции

г(й,ц,у,к)ър(0,4,13,14,15)ь(1,5,7)

карта Карно будет выглядеть так (рис. 3.6):

Рис. 3.6

Карты Карно для функций меньше 4 аргументов называются малые карты Карно, а для функций больше 4 аргументов – большие карты Карно. Большие карты Карно строятся из квадратных карт, число которых зависит от числа аргументов. При этом квадратные карты располагаются так, как клетки в малых картах Карно. Например, карта Карно для функции 5 аргументов строится из двух квадратных карт (рис. 3.7), а для функции 6 аргументов – из четырех (рис. 3.9).

Для карты 5 аргументов клетки можно обозначить следующим образом: пусть в левой квадратной карте аргумент й равен 0, а в правой – 1, столбцы внутри квадратных карт обозначим аргументами цу, а строки – ке5. Тогда номера наборов будут идти так, как показано на рис. 3.7.

43

Цифровая схемотехника

цу

й=0 й=1

Рис. 3.7

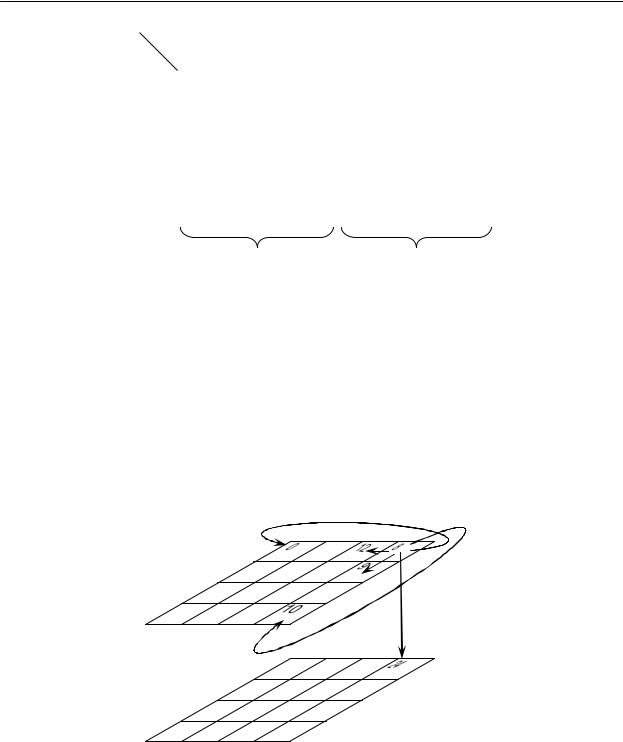
У функции 5 аргументов у каждой клетки должно быть 5 соседних клеток. Чтобы это обеспечить, необходимо выйти за пределы плоскости. При этом 4 соседних клетки находятся в своей квадратной карте, а пятая – в другой квадратной карте на том же самом месте. Для этого нужно каждую квадратную карту свернуть в цилиндр по горизонтали и по вертикали (как в квадратной карте), а затем расположить левую квадратную карту над правой. Например, у клетки номер 8 соседние: 9, 12, 10, 0 и 24. Чтобы клетки 8 и 24 стояли рядом, нужно левую квадратную карту расположить сверху над правой (рис. 3.8).

Рис. 3.8

Карта Карно для функции 6 аргументов строится из четырех квадратных карт (рис. 3.9). При этом у каждой клетки 6 соседних, из них 4 находятся в своей квадратной карте и еще две – в соседних квадратных картах на том же самом месте. Например, у клетки номер 8 четыре соседние в своей квадратной карте (9, 12, 10, 0) и еще две в соседних квадратных картах на том же самом месте (24 и 40).

44