7. Затухающие колебания

В разд. 6.4 была рассмотрена идеальная колебательная система – гармонический осциллятор. Там было показано, что полная энергия гармонического осциллятора постоянна, вследствие чего амплитуда колебаний не изменяется.

В любой реальной колебательной системе существуют потери энергии (например, пружинный маятник испытывает воздействие силы трения, вследствие чего механическая энергия переходит во внутреннюю).

Поскольку энергия реальной колебательной системы умень-шается, должна уменьшаться и амплитуда её колебаний. Это означает, что колебания реального осциллятора затухающие.

7.1. Затухающие колебания пружинного маятника

Циклическая частота идеального пружинного маятника  =, гдеk – коэффициент упругости пружины.

Если на груз кроме упругой будет действовать сила трения, то скорость движения груза уменьшается – ведь сила трения всегда направлена против скорости. Значит, реальный пружинный маятник совершит одно полное колебание за большее время, чем идеальный маятник с таким же коэффициентом упругости. Соот-ветственно период колебаний реального пружинного маятника больше, чем у идеального, а частота меньше.

Период колебаний возрастёт тем больше, чем сильнее трение. И при некоторой определённой силе трения период колебаний может стать бесконечно большим, т. е. колебания могут вообще прекратиться. Выведенная из положения равновесия колеба-тельная система просто плавно вернётся в положение равновесия. Вся сообщённая системе энергия уйдёт на преодоление силы трения.

Теперь рассмотрим поведение пружинного маятника более подробно.

Прежде всего составим уравнение, описывающее эту систему на основании второго закона Ньютона:

.

Пусть действующая на груз сила трения прямо пропорциональна его скорости*

,

где r – коэффициент трения, – скорость груза.

Тогда

или, после деления уравнения на массу груза m,

.

Введём обозначения .

Теперь дифференциальное уравнение можно записать в таком виде:

.

Решение этого уравнения при _o >  имеет вид

,

где .

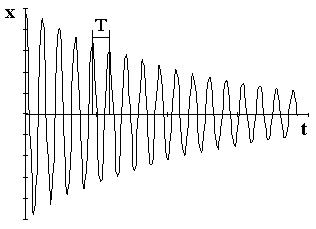
Из решения видно, что маятник совершает колебания (на это ука-зывает наличие cos(t+_o)), ампли-туда которых с течением времени уменьшается по экспоненциаль-ному закону , т. е. такой ма-ятник совершаетзатухающие колебания. График такого коле-бания изображён на рисунке.

_______________________________

* Такое трение называют жидким.

7.2. Затухающие колебания в колебательном контуре

Рассмотрим электрическую цепь, содержащую соленоид, конденсатор и резистор.

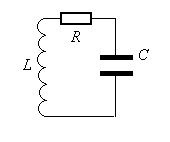
В соответствии со вторым правилом Кирхгофа, сумма разностей потенциалов на элементах контура равна сумме эдс, действующих в рассматриваемом контуре.

В колебательном контуре эдс возни-кает в соленоиде. Это эдс самоиндукции _L.

На обкладках заряженного конден-сатора имеется разность потенциалов. Обозначим её U_C.

Разность потенциалов на концах резистора равна IR.

Тогда уравнение, описывающее колебательный контур, имеет следующий вид:

.

Поскольку напряжение на конденсаторе , аэдс самоиндукции ,

или

;

учитывая, что , получаем

и после деления на L

.

Вводя обозначение и, получаем

,

Мы вновь получили однородное дифференциальное уравнение второго порядка.

Данное уравнение ничем не отличается от того, которое было получено для пружинного маятника в предыдущем разделе. Следовательно, его решение имеет такой же вид: , где.

Это означает, что в колебательном контуре с потерями энергии могут происходить затухающие колебания.