6.3. Сложение гармонических колебаний

6.3.1. Сложение одинаково направленных гармонических колебаний с равными частотами

Пусть некоторая точка участвует одновременно в двух гармонических колебаниях одного направления, имеющих рав-ные частоты.

Каким будет результирующий процесс?

Уравнения, описывающие эти колебания, имеют вид

.

Представим их в векторной форме (см. рисунок).

Сложив графически векторы А₁ и А₂, представляющие первое и второе колебание, получим результирующий вектор А.

Вектор А будет вращаться с той же угловой скоростью, что и складываемые векторы А₁ и А₂. Проекция вектора А на ось х будет изменяться с течением вре-мени по гармоническому закону. Следовательно, результирующий про-цесс представляет собой гармоничес-кое колебание, циклическая частота которого равна циклической частоте складываемых колебаний, амплитуда – А, а начальная фаза – .

Для того чтобы найти значение А, выполним следующие действия:

.

Скалярно умножим вектор А сам на себя:

.

Учитывая, что скалярное произведение вектора на себя равно квадрату его модуля, получаем

и затем

Отсюда

.

Начальная фаза результирующего колебания, как это видно из рисунка, определяется соотношением

.

6.3.2. Сложение одинаково направленных колебаний с разными частотами. Биения

Если частоты складываемых колебаний различны, то векторы А₁ и А₂ будут вращаться с разной скоростью, их взаимное расположение будет меняться. Поэтому с течением времени будут изменяться модуль результирующего вектора и скорость его вращения. Следовательно, амплитуда и циклическая частота результирующего колебания изменяются.

Таким образом, при сложении одинаково направленных гармонических колебаний разных частот возникают негармо-нические колебания.

Полученный вывод интересен ещё и тем, что позволяет увидеть следующее. Если результатом сложения гармонических колебаний разных частот является негармоническое колебание, то негармоническое колебание можно представить как сумму гармонических колебаний разных частот. Это возможно на самом деле и достаточно широко используется как в науке, так и в технике. Раздел физики, изучающий эту проблему, называется гармоническим анализом.

Определённый интерес представляет частный случай – сложение одинаково направленных колебаний с близкими частотами (т. е. ₁  ₂).

Рассмотрим этот случай подробнее. Будем полагать, что начальные фазы и амплитуды складываемых колебаний одинаковы.

В этом случае уравнения, описывающие складываемые колебания имеют вид:

Результирующий процесс будет описываться выражением*

.

Как видно из полученного выражения, результирующий процесс описывается произведением двух косинусов. Цикличес-кая частота первого косинуса очень мала (по условию ₁  ₂), а второго приблизительно равна циклическим частотам склады-ваемых колебаний ₁ и ₂.

Это позволяет трактовать результирующий процесс как колебание с частотой, равной , амплитуда которого медленно меняется по закону.

Такие колебания принято назы-вать биениями.

Частота ₁ – ₂, с которой изме-няется амплитуда результирующе-го колебания, называется частотой биений.

Величина называ-етсяпериодом биений.

6.3.3. Сложение взаимно перпендикулярных колебаний

Пусть материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях:

Точка, участвующая в таких колебаниях, будет одновременно двигаться вдоль двух осей – осей х и у. Поэтому траектория её движения в общем случае может не быть прямолинейной.

__________________________________

* Здесь использована тригонометрическая формула для суммы косинусов: cos x + cos y.

Найдём уравнение, описывающее траекторию частицы, участвующей в этих двух колебаниях, для наиболее простого случая (₁ = ₂).

Для этого исключим из уравнений время t.

Из первого уравнения следует, что

;

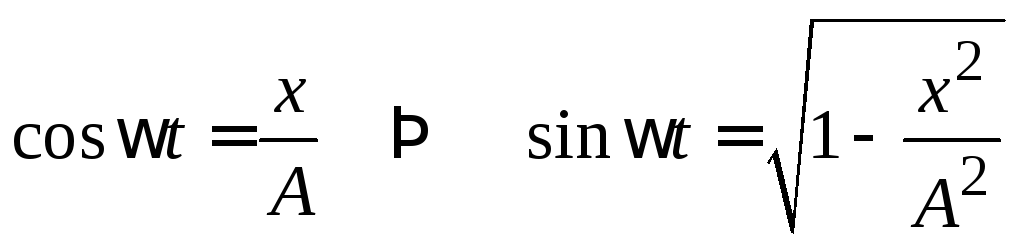а из второго уравнения вытекает

или

,

;

возведем это выражение в квадрат

,

и, наконец, получим уравнение, описывающее траекторию движения частицы, участвующей в двух взаимно перпендику-лярных колебаниях:

.

Мы получили уравнение эллипса, длина и ориентация полуосей которого зависят от амплитуд складываемых коле-баний и от разности фаз . Например, при равных амплитудах и разности фаз в 1 радиан эллипс имеет вид, показанный на рисунке.

Рассмотрим несколько частных слу-чаев.

1. Разность фаз  = 0.

В этом случае уравнение принимает вид

или

.

Это уравнение прямой. Следователь-но, при такой разности фаз точка дви-жется по прямой линии. Её движение представляет собой гармоническое коле-бание с частотой  и амплитудой, равной .

Движение точки будет представлять со-бой гармоническое колебание и в том случае, когда   . Только прямая, вдоль которой будут происходить колебания, будет распо-ложена во втором и четвёртом квадрантах системы координат (проверьте это самосто-ятельно).

2. Разность фаз   /2.

В этом случае уравнение траектории принимает вид:

.

Это уравнение эллипса, оси которого совпадают с осями координат.

Если амплитуды складываемых колебаний будут равны, точка будет двигаться по окружности.

Траектория будет такой же, как и в случае  -/2. Только точка будет двигаться в противоположную сторону.

Если частоты складываемых колебаний различны, форма траектории будет более сложной. Например, если частоты склады-ваемых колебаний отличаются в два раза, то траектория будет иметь вид, показанный на рисунке (если амплитуды складывае-мых колебаний равны и разность их фаз равна 1 радиан).

Кривые, описывающие траектории движения точки, участ-вующей в двух взаимно перпендику-лярных колебаниях, называют фигурами Лиссажу.

Фигуры Лиссажу позволяют опре-делить соотношение частот и разность фаз складываемых колебаний, что до сих пор используется на практике.