6.4.3. Колебательный контур

Рассмотрим электрическую цепь, содержащую идеальный соленоид (это значит, что его сопротивление равно нулю) и конденсатор.

В соответствии со вторым правилом Кирхгофа, сумма разностей потенциалов на элементах контура равна сумме эдс, вклю-чённых в рассматриваемый контур.

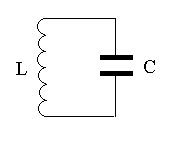
В колебательном контуре эдс возникает в соленоиде. Это эдс самоиндукции _L.

Разность потенциалов на обкладках заря-женного конденсатора обозначим U_C.

Тогда уравнение, описывающее идеальный колебательный контур, имеет следующий вид:

.

Поскольку напряжение на конденсаторе , аэдс самоиндукции ,

или

и после деления на L

.

Вводя обозначение , получаем

.

Мы вновь получили однородное дифференциальное уравнение второго порядка. Следовательно, в идеальном колеба-тельном контуре (т. е. контуре без потерь энергии) происходят гармонические колебания с циклической частотой .

Частота колебаний растёт с уменьшением индуктивности соленоида и ёмкости конденсатора.

Период колебаний в контуре соответственно уменьшается при уменьшенииL и C.

Процессы, протекающие в таком контуре описываются уравнениями

Таким образом, все рассмотренные нами системы отвечают уравнению . Поэтому мы вправе утверждать, что в любой физической системе, описываемой подобным диф-ференциальным уравнением, будут происходить гармонические колебания. Причём изменяться по гармоническому закону будет не только основной параметр, характеризующий систему (т. е.x, , q и т. д.), но и производные этого параметра по времени.

Важно отметить, что для всех систем колебания первой производной по времени от основного параметра опережают по фазе колебания основного параметра на /2, а второй произ-водной – на .

6.5. Энергия гармонического осциллятора

Гармонический осциллятор обладает энергией, за счёт ко-торой и совершает колебания.

Найдём выражения для кинетической, потенциальной и пол-ной механической энергии идеального пружинного маятника.

Кинетическая энергия

.

Потенциальная энергия деформированной пружины

.

Полная механическая энергия

(здесь учтено, что ).

Таким образом, полная механическая энергия идеального пружинного маятника постоянна. Кинетическая и потенциальная энергия постоянно изменяются, причём в положении равновесия кинетическая энергия достигает максимального значения, а потенциальная энергия уменьшается до нуля; при максимальном отклонении груза от положения равновесия всё наоборот – кинетическая энергия равна нулю, а потенциальная максимальна.

В графической форме зависимость потенциальной, кинети-ческой и полной энергии от х имеет вид, показанный на рисунке.

З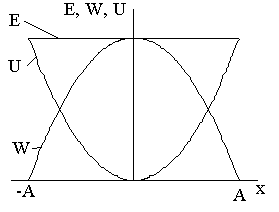ависимость потенциальной, кинетической и полной энергии от времени показана на следующем рисунке (символомТ на рисунке обозначен период гармони-ческого колебания).

Обратите внимание: что кине-тическая и потенциальная энергия изменяются с удвоенной частотой, т. е. с частотой 2_о.

Полученные выводы применимы не только к пружинному маятнику без потерь энергии. Полная энергия любого гармонического осциллятора определяется амплитудой колебаний и упругими свойствами осциллятора и не изменяется с течением времени.

Энергия математического маятника может быть найдена из следующих соображений.

П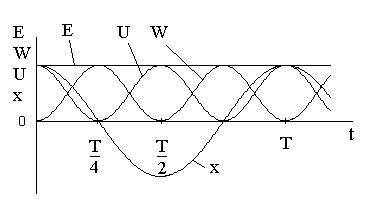ри отклонении математического маятника на малый угол от положения равновесия груз поднимется на высоту h = l – lcos. Потенциальная энергия маятника в этом положении равна U = = mgl(1-cos)=.

Учитывая, что при ма-лых  sin = , получаем

.

Поскольку , потен-циальная энергия математического маятника может быть рассчитана и так:

.

При возвращении маятника к положению равновесия высота груза уменьшается, при этом потенциальная энергия маятника переходит в кинетическую. В положении равновесия потен-циальная энергия уменьшается до нуля, при этом кинетическая достигает максимального значения.

За счёт накопленной кинетической энергии груз продолжит своё движение и вновь поднимется на высоту h, где вся кинетическая энергия перейдёт в потенциальную.

Энергия колебательного контура также может существовать в двух формах: в виде энергии, запасённой в электрическом поле конденсатора, и в виде энергии, запасённой в магнитном поле соленоида.

Как показано в разд. 1.25, энергия заряженного конденсатора равна . Энергия, запасённая в магнитном поле соленоида, равна(см. разд. 5.8).

В тот момент, когда весь заряд сосредоточен на обкладках конденсатора, ток в контуре равен нулю. Вся энергия контура существует в виде энергии заряженного конденсатора. Энергия магнитного поля соленоида равна нулю.

Как только конденсатор начинает разряжаться, через соленоид протекает постепенно возрастающий ток. Соответственно растёт энергия магнитного поля соленоида и уменьшается энергия заряженного конденсатора.

В момент полного разряда конденсатора ток максимален. Поэтому энергия контура существует в виде энергии магнитного поля соленоида.

Ток в контуре после разряда конденсатора протекает именно за счёт энергии магнитного поля. И именно за счёт этой энергии происходит перезарядка конденсатора.