
- •1)Числовые множества. Структура множества действительных чисел. Свойства множества действительных чисел.
- •2)Числовые подмножества. Числовые промежутки. Окрестность точки
- •3) Ограниченные числовые множества, точные грани множеств.
- •4)Определение функции, основные свойства функции.
- •5)Обратные функции, основные свойства функции.
- •6)Определение числовой последовательности и ее предела.
- •7)Теорема о единственности предела числовой последовательности.
- •8)Теорема об ограниченности сходящейся числовой последовательности.
- •9)Арифметические действия над числовыми последовательностями
- •10)Теоремы о предельном переходе в неравенствах
- •11)Бесконечно большие и бесконечно малые последовательности. Связь между ними. Свойства бесконечно малых последовательностей.
- •12)Монотонные последовательности. Теоремы о пределах монотонных последовательностей.
- •13)Доказать , что последовательностьимеет предел.
- •14)Доказать, что
- •15)Подпоследовательности и частичные пределы. Теоремаы о подпоследовательностях.
- •16) Определение придела функции по Коши и по Гейне. Теорема об эквивалентности двух определений придела.
- •17)Односторонние пределы. Необходимое и достаточное условие существования предела функции.
- •18) Первый замечательный предел следствия из него.
- •19)Второй замечательный предел и следствия из него.
- •20)Сравнение бесконечно малых величин.
- •21)Определение порядка б.М. И выделение главной части б.М.
- •22)Вывести таблицу эквивалентных б.М.
- •23)Сравнение б.Б величин .
- •25)Непрерывность функции в точке. Необходимое и достаточное условие непрерывности в точке.
- •26) Классификация точек разрыва.
- •27)Непрерывность функции на множестве. Непрерывность элементарных функций.
- •28)Непрерывность сложной и обратной функции.
- •29) Первая и вторая теоремы Коши.
- •30) Первая и вторая теоремы Вейерштрасса.
- •31)Определение производной. Геометрический и физический смысл.
- •32)Односторонние производные. Необходимое и достаточное условие существования производной.
- •33)Правила вычисления производных от суммы , произведения и частного.
- •35)Производная обратной функции.
- •36) Производная функции заданной параметрически.
- •37)Производная неявно заданной функции.
- •39) Связь между непрерывностью и дифференцируемостью ф-и.
- •40) Определение дифференциала ф-и. Геометрический смысл дифференциала. Правила вычисления дифференциала.
- •43)Повторное дифференцирование в дифференциалах. Нарушение инвариантности формы высших дифференциалов.
- •44) Формула Тейлора для многочлена.
- •45)Формула Тейлора для произвольной ф-и.
- •46)Стандартные разложения. Определение числа e с точностью до 0,001.
- •47) Достаточное усл-е монотонности ф-и.
- •49) Достаточные условия экстремумафункции в точке
- •50) Достаточные условия выпуклости (вогнутости) ф-и. Определение выпуклой и вогнутой ф-и.
- •51) Точки перегиба. Достаточное условие точки перегиба.
- •52) Определение неопределенного интеграла. Свойства неопределенного интеграла.
- •53)Вывести таблицу интегралов из определения неопределенного интеграла .
- •54) Замена переменной в неопределенном интеграле.
- •55)Интегрирование по частям в неопределенном интеграле.
- •56. Понятие о рациональных и дробно-рациональных функциях. Разложение правильной рациональной дроби на сумму простейших дробей.
- •57) Интегрирование простейших дробей.
- •58. Вывод рекуррентной формулы.
- •60. Интегрирование дифференциального бинома. Подстановки Чебышева.
- •61. Подстановки Эйлера.
- •62. Интегрирование тригонометрических функций.
- •63. Определение интеграла Римана. Функции, интегрируемые по Риману.
- •64. Свойства интеграла Римана, выражаемые равенствами.
- •65. Свойства интеграла Римана, выражаемые равенствами.
- •66. Основная теорема интегрального исчисления.
- •67. Замена переменной в определенном интеграле.
- •68) Интегрирование по частям в определенном интеграле.
- •69) Вычисление площадей плоских фигур в декартовых координатах.
- •70) Площадь плоской фигуры в параметрическом виде.
- •71) Площадь плоской фигуры в полярных координатах.
- •72. Вычисление длины дуги в декартовых координатах.
- •73. Вычисление длины дуги в параметрическом виде.
- •74. Вычисление длины дуги в полярных координатах.
- •75) Понятия о двух типах несобственных интегралов
46)Стандартные разложения. Определение числа e с точностью до 0,001.
Стандартное разложение получено по ф-ле (4) при x0=0.
1. y=ex |x=0 = 1, y’=ex |x=0 = 1, y’’=ex |x=0 = 1, … , y(n) = ex |x=0 = 1.
ex
= 1 +
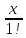 +
+ + … +
+ … +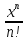 + 0(xn),
Rn(x)
=
+ 0(xn),
Rn(x)
=
 *xn+1,
0<С<1 – остат. член в форме Лагранжа
для показательной ф-и.
*xn+1,
0<С<1 – остат. член в форме Лагранжа
для показательной ф-и.
y(n+1) = ex | x=C = eC
2. y=sinx |x=0 = 0, y’=cosx |x=0 = 1, y’’=-sinx |x=0 = 0, y’’’=-cosx |x=0 = -1, yiv=sinx |x=0 = 0, yv=cosx |x=0 = 1, yvi=-sinx |x=0 = 0, yvii=-cosx |x=0 = -1
sinx
= x –
 +
+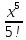 –
– + … + (-1)n-1*
+ … + (-1)n-1* + 0(x2n).
+ 0(x2n).
Rn(x)
= (-1)n
*
 *xn+1
– остат. член в форме Лагранжа для
y=sinx.
*xn+1
– остат. член в форме Лагранжа для
y=sinx.
Т.к. ф-я y=sinx – нечетн., то в разлож. по ф-ле Тейлора содерж. только нечетн. степени x.
3. y=cosx |x=0 = 1, y’=-sinx |x=0 = 0, y’’=-cosx |x=0 = -1, y’’’=sinx |x=0 = 0, yiv=cosx |x=0 = 1
cosx
= 1 -
 +
+ -
- + … + (-1)n*
+ … + (-1)n* + 0(x2n+1)
+ 0(x2n+1)
Т.к. ф-я y=cosx – четн., то в разлож. по ф-ле Тейлора содерж. только четн. степени x.
4. αϵR. y=(1+x)α |x=0 = 1, y’=α(1+x)α-1 |x=0 = α , y’’=α(α-1)(1+x)α-2 |x=0 = α(α-1)
y’’’=α(α -1)( α -2)(1+x)α-3 |x=0 = α(α-1)( α-2), y(n) = (α(α-1)( α-2)…(1+x)α-n |x=0 = α(α-1)…(α-n+1)
(1+x)α
= 1+
 x
+
x
+
 +
+ + … +
+ … + + 0(xn)
биномиальное разлож-е
+ 0(xn)
биномиальное разлож-е
5.
y=ln(1+x)
|x=0
= 0, y’
=
 |x=0
= 1, y’’
=
|x=0
= 1, y’’
=
 |x=0
= -1, y’’’
=
|x=0
= -1, y’’’
=
 |x=0
= 2! , yiv
=
|x=0
= 2! , yiv
=
 |x=0
= -3!, …, yn
=
|x=0
= -3!, …, yn
=
 |x=0
= (-1)n-11*2*…*(n-1)
= (-1)n-1(n-1)!
|x=0
= (-1)n-11*2*…*(n-1)
= (-1)n-1(n-1)!
ln(1+x)
= x -
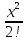 +
+ -
- + … +
+ … + + 0(xn)
= x -
+ 0(xn)
= x -
 +
+ -
- + …+
+ …+
 + 0(xn).
+ 0(xn).
Определение числа e с точностью до 0,001.
Воспользуемся стандартным разложением ex в форме Лагранжа:
ex
= 1 +
 +
+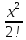 +
+ + … +
+ … + +
+ *xn+1.
*xn+1.
Пусть
x=1: e = 2 +
 +
+ + … +
+ … + +
+ , Rn
=
, Rn
=
 <
< <0,001 => eC<e<3
<0,001 => eC<e<3
При
n=5 => Rn
=
 =
= ≈ 0,00416
≈ 0,00416
При
n=6
=> Rn
=
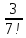 ≈ 0,00059 < 0,001
≈ 0,00059 < 0,001
e
= 2 +
 +
+ +
+ +
+ +
+ ≈ 2,718
≈ 2,718
________________________________________________________________________
47) Достаточное усл-е монотонности ф-и.
Теорема: пусть ф-я f(x) дифференцируема на (a,b), если:
f'(x)>0, то f(x) монот. возраст. на (a,b)
f’(x)<0, то f(x) монот. убыв. на (a,b)
f’(x)≡0, при
 xϵ(a,b),то
f(x) = const.
xϵ(a,b),то
f(x) = const.
Док-во: выберем произвольный отрезок [x1,x2]c(a,b) и на этом отрезке запишем ф-лу конечных приращений Лагранжа, т.е.ƎѮϵ(x1,x2),
f(x2) – f(x1) = f’(Ѯ)(x2-x1) (*)
пусть f’(x)>0 при xϵ(a,b), то f’(Ѯ)>0. Тогда из (*) получаем f(x2) – f(x1)>0 => f(x2) > f(x1)
 x2>x1,
т.е. f(x)
монотонно возраст. на (a,b)
x2>x1,
т.е. f(x)
монотонно возраст. на (a,b)пусть f’(x)<0 при xϵ(a,b), то f’(Ѯ)<0. Тогда из (*) получаем f(x2) – f(x1)<0 => f(x2)<f(x1)
 x2<x1,
т.е.
f(x)
монотонно убывает на (a,b)
x2<x1,
т.е.
f(x)
монотонно убывает на (a,b)пусть f’(x)≡0 при xϵ(a,b), то f’(Ѯ)≡0. Тогда из (*) получаем f(x2) – f(x1)=0 => f(x2)=f(x1), т.е. f(x) постоянная на (a,b).
________________________________________________________________________
48)Определение локального экстремума. Необходимое условие экстремума.
Определение локального экстремума.
Пусть ф-я f(x) определена на (a,b).
Опред.1:
ф-я f(x)
имеет локальный максимум в т. x0ϵ(a,b),
если Ǝ такая окр-ть этой точки, что все
значения ф-и в этой окр-ти будут меньше
значений ф-и в т. x0,
т.е. (Ǝƃ>0)(
![]() xϵ(a,b),|x-x0|<ƃ):f(x)<f(x0).
Если выполняется неравенство f(x)≤f(x0),
то такой максимум называется нестрогим.
xϵ(a,b),|x-x0|<ƃ):f(x)<f(x0).
Если выполняется неравенство f(x)≤f(x0),
то такой максимум называется нестрогим.
Опред.2:
ф-я f(x)
имеет в т. x0ϵ(a,b)
локальный минимум, если существует
такая окр-ть этой точки, что все значения
ф-и в этой окр-ти будут больше значений
ф-и в т. x0,
т.е. (Ǝƃ>0)(
![]() xϵ(a,b),|x-x0|<ƃ):f(x)>f(x0).
Если выполняется неравенство f(x)≥f(x0),
то такой минимум называется нестрогим.
xϵ(a,b),|x-x0|<ƃ):f(x)>f(x0).
Если выполняется неравенство f(x)≥f(x0),
то такой минимум называется нестрогим.
Точки лок. макс. и мин. назыв. точками экстремума.
Необходимое условие экстремума.
Если f(x) имеет локал. Экстремум в т. x0ϵ(a,b), то f’(x)=0, либо f’(x)=∞, либо не существует.
Док-во: предположим, что т. x0ϵ(a,b) – точка локал. Максимума и пусть существует f’(x). Покажем что f’(x)=0.
Запишем
определение точки максимума: (Ǝƃ>0)(
![]() xϵ(a,b),
x0–ƃ<x<
x0+ƃ):f(x0)≥f(x)
и составим отношение
xϵ(a,b),
x0–ƃ<x<
x0+ƃ):f(x0)≥f(x)
и составим отношение
 :
:
пусть x→x0, x<x0:
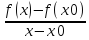 ≥0
≥0
рассмотрим
 =f-‘(x0)≥0
=f-‘(x0)≥0
пусть x→x0, x>x0:
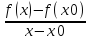 ≤0
≤0
 =
f+‘(x0)≤0.
=
f+‘(x0)≤0.
Мы предположили, что Ǝf’(x0) => f-‘(x0) = f+’(x0) = f’(x0) => f(x0)=0.
Аналогично доказывается, если x0 – точка локал. минимума и существует f’(x0).
Случай,
когда x0
- точка локал. экстремума и либо f’(x0)=∞,
либо не сущ. Покажем на примерах.![]()
![]()
y=|x|, x=0 – т. min
f’(0) не существует
y=1-|x|, x=0 – т.max
f’(0)
не существует![]()

y=

y’= ,
y’(0)=∞
,
y’(0)=∞
x=0 – т. min
y=

y’= ,
y’(0)=∞, x=0 – т.
max
,
y’(0)=∞, x=0 – т.
max
теорема дает необходимое, но не достаточное усл-е экстремума. Необходимое усл-е экстремума исп. для нахождения точек, в которых экстремум может быть, а может не быть. Такие точки назыв. точками подозрительными на экстремум.
________________________________________________________________________
