3. Матрицы и их свойства

Определение: Матрицей размерности mxn (m на n) называют таблицу чисел, которая состоит из m строк и n столбцов.

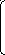
a₁₁ a₁₂ a₁₃ …… a_1n

a₂₁ a₂₂ a₂₃ …… a_2n

…………………………….

a_m1 a_m2 a_m3 …… a_mn

Определение: Если в матрице число строк совпадает с числом столбцов (m=n), то матрица называется квадратной порядка n и для квадратных матриц вводят понятие определителя матрицы (т.е. определителя для элементов данной матрицы).

Квадратная матрица называется единичной, если по главной диагонали матрицы стоят единицы, а все остальные элементы матрицы равны 0 (нулю).

1 0 - единичная 1 0 0 - единичная

E = 0 1 матрица E = 0 1 0 матрица

2-го порядка 0 0 1 3-го порядка

Матрица, полученная из матрицы "А" заменой строк столбцами с сохранением нумерации, называется транспонированной матрицей по отношению к матрице "А" и обозначается A^T.

a₁₁ a₁₂ a₁₁ a₂₁

A = a₂₁ a₂₂ A^T = a₁₂ a₂₂

4. Операции над матрицами

Определение: Матрица А равна матрице В, если в этих матрицах равны между собой все соответствующие элементы:

a_ij = b_ij для всех i,j

Матрицы одинакового порядка можно складывать и вычитать.

1. Сумма (разность) двух матриц:

a₁₁ a₁₂ b₁₁ b₂₁

A = a₂₁ a₂₂ B = b₁₂ b₂₂

a₁₁  b₁₁ a₁₂  b₁₂

A  B = a₂₁  b₂₁ a₂₂  b₂₂

2. Умножение матрицы на число, отличное от нуля:

*a₁₁ *a₁₂

*A = *a₂₁ *a₂₂ ,   0

3. Произведение двух матриц:

Умножать можно только те матрицы, для которых выполняется условие: число столбцов первой матрицы равно числу строк второй матрицы.

Сумма произведений элементов первой строки первой матрицы на элементы первого столбца второй матрицы определит элемент С₁₁ матрицы произведения. И таким образом для всех Cij элементов произведения:

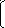
a₁₁ a₁₂ b₁₁ b₁₂

A*B = a₂₁ a₂₂ * b₂₁ b₂₂ =

a₁₁ * b₁₁ + a₁₂ * b₂₁ a₁₁ * b₁₂ + a₁₂ * b₂₂

= a₂₁ * b₁₁ + a₂₂ * b₂₁ a₂₁ * b₁₂ + a₂₂ * b₂₂

Пример:

1 1

1 2 3 * 2 1 1+4+9 1+2+12 14 15

A*B = 4 5 6 3 4 = 4+10+18 4+5+24 = 32 33

Для суммы и произведения матриц справедливы следующие соотношения:

1) A+B=B+A 4) A+(B+C) = (A+B)+C

2) C*(A+B)=C*A+C*B 5) (*A)*B = *(A*B)

3) (A*B)*C=A*(B*C) 6) ( + )*A = *A+*A

7) *(A+B) = *A+*B

8) A*E=E*A=A , где E –единичная матрица.

Для матриц, в общем случае, умножение не перестановочно:

A*B  B*A

Определение: Матрица А^-1 называется обратной для квадратной матрицы А, если выполняется следующее соотношение:

А*А^-1=А^-1*А = Е

Понятие обратной матрицы вводится только для квадратных матриц.

Теорема: Матрица А имеет обратную тогда и только тогда, когда определитель матрицы не равен нулю:

1 A₁₁ A₂₁ A₃₁

A^-1 = * A₁₂ A₂₂ A₃₂

A A₁₃ A₂₃ A₃₃

a₁₁ a₁₂ a₁₃

для A = a₂₁ a₂₂ a₂₃ A – определитель матрицы А

a₃₁ a₃₂ a₃₃

Доказательство:

Чтобы доказать, что матрица А^-1 является обратной для матрицы А, необходимо показать выполнение следующего равенства:

А*А^-1=А^-1*А=Е

1 A₁₁ A₂₁ A₃₁ a₁₁ a₁₂ a₁₃ 1

A^-1 *A = * A₁₂ A₂₂ A₃₂ * a₂₁ a₂₂ a₂₃ = *

A A₁₃ A₂₃ A₃₃ a₃₁ a₃₂ a₃₃ A

A₁₁*a₁₁+A₂₁*a₂₁+A₃₁*a₃₁ A₁₁*a₁₂+A₂₁*a₂₂+A₃₁*a₃₂ A₁₁*a₁₃+A₂₁*a₂₃+A₃₁*a₃₃

* A₁₂*a₁₁+A₂₂*a₂₁+A₃₂*a₃₁ A₁₂*a₁₂+A₂₂*a₂₂+A₃₂*a₃₂ A₁₂*a₁₃+A₂₂*a₂₃+A₃₂*a₃₃ =

A₁₃*a₁₁+A₂₃*a₂₁+A₃₃*a₃₁ A₁₃*a₁₂+A₂₃*a₂₂+A₃₃*a₃₂ A₁₃*a₁₃+A₂₃*a₂₃+A₃₃*a₃₃

1 A 0 0 1 0 0

= * 0 A 0 = 0 1 0

A 0 0 A 0 0 1

что и требовалось доказать.

Пример: Вычислить матрицу, обратную данной:

1 1 -1 1 1 -1

A = 4 -3 1 ; A = 4 -3 1 = 1*(-3)*(-1) + 1*1*2 + 4*1*(-1) -

2 1 -1 2 1 -1

- 2*(-3)*(-1) – 1*1*1 – 4*1*(-1) = 3+2-4-6-1+4 = -2

-3 1 4 1

A₁₁ = (-1)¹⁺¹ 1 -1 = 2 ; A₁₂ = (-1)¹⁺² 2 -1 = 6;

4 -3 1 -1

A₁₃ = (-1)¹⁺³ 2 1 = 10 ; A₂₁ = (-1)²⁺¹ 1 -1 = 0;

1 -1 1 1

A₂₂ = (-1)²⁺² 2 -1 = 1 ; A₂₃ = (-1)²⁺³ 2 1 = 1;

1 -1 1 -1

A₃₁ = (-1)³⁺¹ -3 1 = - 2 ; A₃₂ = (-1)³⁺² 4 1 = - 5;

1 1

A₃₃ = (-1)³⁺³ 4 -3 = - 7

1 A₁₁ A₂₁ A₃₁ 1 2 0 -2

A^-1 = * A₁₂ A₂₂ A₃₂ = - * 6 1 -5

A A₁₃ A₂₃ A₃₃ 2 10 1 -7