4. Условие параллельности и перпендикулярности двух прямых

Пусть в пространстве заданы прямые:

(x – x₁) (y – y₁) (z – z₁)

l₁: = =

m₁ n₁ p₁

(x – x₂) (y – y₂) (z – z₂)

l₂: = =

m₂ n₂ p₂

1) l₁l₂ S₁S₂  M₁M₂ m₁/m₂ = n₁/n₂ = p₁/p₂ ,

где M₁(x₁ ,y₁,z₁), M₂(x₂,y₂,z₂) точки на прямых. Прямые не совпадают, иначе их, строго говоря, нельзя назвать параллельными.

2) l₁  l₂ S₁  S₂ S₁ * S₂ = 0 , т.е. m₁*m₂ + n₁*n₂ + p₁*p₂ = 0

5. Угол между двумя прямыми

 = ( l₁, l₂ ) = (S₁, S₂)

cos  = (S₁*S₂) / S₁ *S₂  =

= (m₁*m₂+n₁*n₂+p₁*p₂) / ( ( m₁² +n₁² +p₁²) *  ( m₂² +n₂² +p₂²) )

6. Угол между прямой и плоскостью.Условия параллельности и перпендикулярности прямой и плоскости

Пусть дана прямая l и плоскость 

(x – x₁) (y – y₁) (z – z₁)

l: = =

m n p  = ( , l )

: A*x + B*y + C*z + D = 0 (90⁰-) = (N, S )

cos(90⁰ - ) = sin  = |A*m+B*n+C*p| / (( A² +B² +C²) *  ( m² +n² +p²) ) ,

где N = (A, B, C), S = (m,n,p)

Знак модуля позволяет распространить выражение на случай тупого угла.

1. Пусть прямая l параллельна плоскости  :

l N  S N *S = A*m + B*n + C*p = 0

A*x₁ +B*y₁ +C*z₁ +D  0

N M₁(x₁ ,y₁,z₁) – точка на прямой.

Второе условие исключает вариант

 расположения прямой на плоскости.

l Точка M₁(x₁ ,y₁,z₁) не принадлежит

плоскости. Прямая не в плоскости.

S

2) Пусть прямаяl перпендикулярна плоскости  : l   NS

l

N NS A/m = B/n = C/p

S



4. Кривые второго порядка на плоскости

Определение: Окружностью называют множество точек плоскости равноудаленных от данной точки, называемой центром, на заданное расстояние, называемое радиусом окружности.

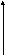Y

R (x – a)² + (y – b)² = R² - уравнение окружности

a O

где O(a,b) – координаты центра окружности.

0 b X R - радиус окружности.

Определение: Эллипсом называют множество точек плоскости, сумма расстояний каждой из которых до двух точек, называемых фокусами эллипса, есть величина постоянная и большая, чем расстояние между фокусами.

Уравнение эллипса: x²/a² + y²/b² = 1

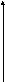Y

B₁ b M A₁, A₂, B₁, B₂ – вершины эллипса

A₁ F₁ F₂ A₂ X отрезок A₁A₂ – большая ось эллипса.

-a -c O +c a OA₂ – большая полуось эллипса.

B2 -b B₁B₂ –малая ось эллипса

OВ₁ – малая полуось эллипса.

F₁, F₂ – фокусы эллипса.

F₁M, F₂M – фокальные радиусы.

По определению F₁M + F₂M = 2*a > F₁F₂ = 2*c

2*a > 2*c

b² = a² – c²

c = F₁F₂ / 2

Эксцентриситетом эллипса называют отношение величины с к величине а  = c/a < 1

Определение: Гиперболой называют множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до 2-х заданных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

x² y²

 = 1 - уравнение гиперболы.

a² b²

Y

M

-a B₁ a A₁, A₂ – вершины гиперболы

F₁ b F₂ A₁A₂ - действительная ось

A₁A₂Xгиперболы

B₂ b B₁B₂ - мнимая ось гиперболы.

F₁, F₂ - фокусы гиперболы.

F₁M – F₂M  = 2*a < F₁F₂ = 2*c ,

b² = c² – a² , эксцентриситет  = c/a > 1

Определение: Параболой называют множество точек плоскости, каждая из которых находится на одинаковом расстоянии от некоторой точки, называемой фокусом и от заданной прямой, называемой директрисой.

Y

FM = FN

F(p/2,0) – фокус параболы

x = -p/2 –директриса

p/2 0 F X Уравнение параболы:

+ p/2

y² = 2*p*x ,

N M

где p – параметр параболы.

СОДЕРЖАНИЕ

1. ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ 3

1.1 Множества чисел и их обозначения 3

1.2 Основные операции над множествами 4

1.3 Логические символы 4

1.4 Специальные математические символы 4

2. ЛИНЕЙНАЯ АЛГЕБРА 5

2.1 Определители и их свойства 5

2.2 Свойства определителей 6

2.3 Матрицы и их свойства 9

2.4 Операции над матрицами 9

2.5 Экономическая интерпретация действий над матрицами 11

2.6 Системы линейных уравнений 12

2.7 Решение систем линейных уравнений при помощи формул Крамера 13

2.8 Решение систем линейных уравнений матричным способом 14

2.9 Линейные системы общего вида 15

2.10 Решение систем линейных уравнений методом Гаусса. 18

2.11 Экономическая интерпретация систем линейных уравнений 20

3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ 21

3.1 Основные понятия 21

3.2 Действия над векторами 21

3.3 Свойства действий над векторами 22

3.4 Проекция вектора на ось 22

3.5 Координаты точки на числовой оси, на плоскости и в пространстве 23

3.6 Теоремы о проекции вектора на ось 24

3.7 Длина вектора. Направляющие косинусы вектора 25

3.8 Понятие базиса. Разложение вектора по базису 26

3.9 Скалярное произведение векторов 27

3.9.1 Свойства скалярного произведения. 27

3.9.2 Следствия из свойств скалярного произведения. 27

3.9.3 Скалярные произведения векторов через координаты 28

3.10 Векторное произведение двух векторов 28

3.11 Смешанное произведение векторов 29

3.11.1 Свойства смешанного произведения 30

3.12 Геометрический смысл смешанного произведения векторов 30

3.13 N-мерные векторы 31

3.14 Линейная зависимость (независимость) системы векторов 32

3.15 Разложение вектора по некоторому базису 32

4. ЭЛЕМЕНТЫ аналитическОЙ геометриИ 33

4.1 Прямая линия на плоскости и в пространстве. Прямая на плоскости 33

4.1.1 Уравнение прямой, проходящей через данную точку, с данным угловым коэффициентом 33

4.1.2 Уравнение прямой, проходящей через две данные точки 34

4.1.3 Уравнение прямой, проходящей через две данные точки, если y1=y2 34

4.1.4 Уравнение прямой, проходящей через две данные точки, если x1=x2 34

4.1.5 Угол между двумя прямыми 34

4.1.6 Условия параллельности и перпендикулярности двух прямых 35

4.1.7 Общее уравнение прямой 35

4.1.8 Частные случаи общего уравнения прямой 35

4.1.9 Уравнение прямой на плоскости в отрезках 36

4.1.10 Расстояние от точки до прямой 36

4.2 Уравнение плоскости в пространстве 36

4.2.1 Угол между плоскостями 37

4.2.2 Условия параллельности и перпендикулярности 2-х плоскостей 37

4.2.3 Расстояние от плоскости до точки 37

4.2.4 Уравнение плоскости, проходящей через 3 заданные точки. 37

4.3 Прямая линия в пространстве 38

4.3.1 Параметрическое уравнение прямой в пространстве и каноническое уравнение прямой в пространстве 38

4.3.2 Уравнение прямой в пространстве, проходящей через 2 заданные точки 38

4.3.3 Прямая, как линия пересечения двух плоскостей 39

4.3.4 Условие параллельности и перпендикулярности двух прямых 39

4.3.5 Угол между двумя прямыми 40

4.3.6 Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости 40

4.4 Кривые второго порядка на плоскости 41

44