6. Оценить, как изменится величина относительной погрешности, полученной в п. 2 для формулы (7.1), если не учитывать радиус нити и пренебречь единицей по сравнению с величиной без-

размерного комплекса 2h / gt2 . По результатам оценки сделать выводы о возможности сделанных упрощений.

Вопросы и задания для допуска к лабораторной работе

1.Дать определения момента инерции твёрдого тела и момента силы относительно заданной оси. Как определяется направление момента силы?

2.Записать основной закон динамики для твёрдого тела. Как направлено угловое ускорение при вращательном движении твёрдого тела?

3.Сформулировать коротко суть метода, применяющегося в лабораторной работе, для определения момента инерции маятника Максвелла.

Вопросы и задания к защите лабораторной работы

1.Провести аналогию между характеристиками вращательного и поступательного движения.

2.Доказать, что W Wк U mgh0 , решив совместно урав-

нения (7.1) и (7.2).

3. Исходя из определения момента инерции: I r 2dm , вы-

вести формулу для момента инерции диска радиуса R : I 0,5mR2 .

4. Вывести формулу относительной погрешности для форму-

лы (7.1).

Библиогр.: [1]; [2, § 36, 37, 39, 42, 43, 54]; [3, § 33-37]; [5, § 4.1-4.3].

ЛАБОРАТОРНАЯ РАБОТА № 8

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДЫХ ТЕЛ С ПОМОЩЬЮ КРУТИЛЬНЫХ КОЛЕБАНИЙ

62

Цель работы – изучить законы динамики вращательного движения твёрдого тела; экспериментально определить моменты инерции твёрдых тел относительно различных осей вращения.

Приборы и принадлежности: крутильный маятник FPM-05,

твёрдые тела различной формы, секундомер.

Краткие сведения из теории

При описании вращательного движения твёрдого тела вводится понятие момента инерции – физической величины, характеризующей распределение масс в теле относительно оси вращения и являющейся мерой инертности тела при вращательном движении. Моментом инерции тела относительно некоторой оси называется величина, равная сумме произведений элементарных масс на квадраты их расстояний от данной оси:

I mi ri2 .

i

Если вещество в теле распределено непрерывно, то вычисление его момента инерции сводится к вычислению интеграла:

I r2dm,

где dm – масса элемента объёма тела, находящегося на расстоянии r от оси вращения.

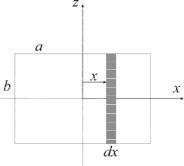
Рассмотрим в качестве примера плоскую прямоугольную пластинку со сторонами a и b и массой

лится как

63

В ряде случаев нахождение момента инерции значительно упрощается, если воспользоваться теоремой Штейнера: момент инерции тела относительно произвольной оси z равен моменту

инерции IzС относительно оси zс , проходящей через центр масс

тела и параллельной данной, плюс произведение массы тела на квадрат расстояния a между осями:

Iz IzС ma2.

Найдем теперь момент инерции однородного прямоугольного параллелепипеда относительно оси z , проходящей через его центр масс (рис. 8.2).

Для этого разобьём параллелепипед на бесконечно тонкие пластинки, параллельные плоскости zx , толщиной dy и массой

dm Vm dV ma dy каждая. Согласно теореме Штейнера момент

инерции такой пластинки относительно оси z равен: dI 121 b2dm y2dm 121 b2 ma dy ma y2dy.

Рис. 8.2

64

Аналогично можно показать, что моменты инерции параллелепипеда относительно осей x и y определяются формулами

Момент инерции тела относительно произвольно ориентированной оси ν, проходящей через центр масс тела, определяется соотношением

где cos , cos , cos – направляющие косинусы (рис. 8.3).

Рис. 8.3

Для момента инерции однородного прямоугольного параллелепипеда относительно оси АВ (диагональ параллелепипеда)

65

Тогда, подставив (8.1) – (8.3) в (8.4), с учётом (8.5) получим

Описание и принцип работы экспериментальной установки. Вывод расчётной формулы

Для определения момента инерции тел используется крутильный маятник (рис. 8.4), основным элементом которого является рамка 1, подвешенная с помощью двух вертикально закреплённых проволок 3. Для регистрации её колебаний рамка снабжена флажком 2.

Крутильные колебания представляют собой один из видов колебаний упругих систем, при котором отдельные элементы системы (в данном случае – проволока) испытывают деформацию кручения.

Уравнение динамики вращательного движения твёрдого тела с моментом инерции I относительно фиксированной оси под действием момента M упругих сил можно

Рис. 8.4

I k 0 . Это уравнение гармонических колебаний с периодом

T 2 kI . Следовательно, определив экспериментально период

Момент инерции рамки крутильного маятника определяется по аналогичной формуле:

тильного маятника, относительно различных осей.

Суммарный момент инерции рамки и закреплённого в ней тела равен: I Ii I0 Соответственно период крутильных колебаний

Тогда, измерив период Ti , можно рассчитать момент инерции тела относительно i-й оси:

Согласно теории упругих деформаций для проволоки круглого сечения радиусом R и длиной L модуль кручения равен

k R4G / 2L , где G – модуль сдвига материала проволоки. Для крутильного маятника с двумя проволоками, используемого в работе,

для стали.

Порядок выполнения работы

67

1.Нажав кнопку «Сеть», включить установку. На лицевой панели секундомера должны загореться цифровые индикаторы. Флажок рамки (позиция 2 на рис. 8.4) должен пересекать оптическую ось фотодатчика.

2.Измерить время n = 10 колебаний рамки. Для этого отклонить рамку рукой на угол (4÷5)° и отпустить. Нажать кнопку «Сброс». Дождаться появления на циферблате секундомера цифры «9» и нажать клавишу «Стоп». Секундомер остановится, отсчитав

время t0 десяти колебаний. Записать измеренное время в табл. 8.1. 3. Повторить п. 2 пять раз.

R = ….. м; l1 = …… м; l2 = ….. м.

Таблица 8.1

…

4.Отключить прибор.

5.Установить в рамку маятника образец (параллелепипед). Для этого отпустить гайки цанговых зажимов на подвижной рамке, приподнять планку и осторожно вставить образец так, чтобы острия рамки входили в углубления на образце по нужной оси (x, y, z или АB (рис.8.3)).

6.Выполнить пп. 2-3 для всех указанных осей (x, y, z, АB (см. рис.8.3)). Результаты заносить в таблицы типа табл. 8.2, каждый раз меняя только наименование исследуемой оси (x, y, АB).

Таблица 8.2

Обработка и анализ экспериментальных данных

1. По формуле (8.10) вычислить модуль кручения k.

68

2.По данным табл. 8.1 для каждого измерения вычислить период колебаний T0 tn0 и момент инерции рамки I0 по формуле

(8.8).

3.По данным табл. 8.2 вычислить периоды колебаний Ti tni

относительно различных осей.

4.Вычислить по формуле (8.9) моменты инерции Ii образца относительно осей x, y, z и AB. Для каждой из осей усреднить полученные значения Ii, оценить погрешность по разбросу значений

изаписать окончательный результат.

5.Провести оценочные расчёты моментов инерции Ii выбранного образца (параллелепипеда) без учёта скоса вершин относительно осей x, y, z и AB по формулам (8.1) – (8.4). При расчётах

использовать следующие данные: a = b= 0,05 м, с = 0,1 м

т= 1,94 кг.

6.Сравнить результаты п. 5 с опытными данными (результатами п. 4).

Вопросы и задания для допуска к лабораторной работе

1.Записать: уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси; теорему Штейнера.

2.Дать определение момента инерции твёрдого тела.

3.Сформулировать коротко суть метода, применяющегося в лабораторной работе, для определения момента инерции твёрдых тел с помощью крутильного маятника.

Вопросы и задания к защите лабораторной работы

1.Вывести формулу момента инерции однородного прямоугольного параллелепипеда относительно оси x (см. рис. 8.3).

2.Доказать, что решение уравнения I k 0 приводит к

Библиогр.: [1]; [2, § 38, 39, 43]; [3, § 33-36, 46, 79]; [5, § 4.1-4.3, 27.2].

69