2.Записать уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси, теорему Штейнера

изакон сохранения момента импульса.

3.Сформулировать коротко суть метода, применяющегося в лабораторной работе, для определения момента инерции крутильного маятника и модуля кручения нити. От каких величин зависит модуль кручения?

Вопросы и задания к защите лабораторной работы

1.Записать законы сохранения для абсолютно упругого соударения в системе «математический–крутильный маятники».

2.Доказать, что решением уравнения 02 0 является

выражение 0 cos( 0t ) .

3. Могут ли синусы углов, входящие в формулу (9.8), быть заменены самими углами? Как это сказалось бы на точности расчёта момента инерции крутильного маятника.

Библиогр.: [1]; [2, § 36, 38, 39, 43, 54]; [3, § 33-36, 46, 79]; [5, § 4.1-4.3, 27.1, 27.2].

ЛАБОРАТОРНЫЕ РАБОТЫ № 10–12

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЁМКОСТЕЙ ИДЕАЛЬНОГО ГАЗА ПРИ ПОСТОЯННЫХ ДАВЛЕНИИ

И ОБЪЁМЕ C p CV РАЗЛИЧНЫМИ МЕТОДАМИ

Краткие сведения из теории

Законом сохранения энергии для систем, в которых существенное значение имеют тепловые процессы, является первое начало термодинамики: теплота, сообщённая системе, расходуется на изменение её внутренней энергии U и на совершение этой сис-

77

темой работы A против внешних сил: Q U A . Более важной является дифференциальная форма этого закона:

– неполный дифференциал) обусловлено различием смысла функций: внутренняя энергия является функцией состояния ( dU 0 ),

а теплота и работа – функциями процесса ( Q 0; A 0 ).

Теплоёмкостью называется величина, равная отношению количества теплоты δQ, сообщаемого телу при бесконечно малом изменении его состояния в каком-либо процессе, к соответствую-

щему изменению dТ температуры этого тела: Cтела Q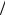dT . Если эта величина рассчитывается на единицу массы, теплоёмкость называется удельной (обозначается «c» и измеряется в Дж/кг·К). Если же расчёт ведётся на 1 моль вещества, теплоёмкость называется молярной (обозначается « C » и измеряется в Дж/моль·К).

Из определения теплоёмкости видно, что она, так же как иQ , является функцией процесса и, следовательно, понятие тепло-

ёмкости не имеет смысла, пока не задан путь, на котором система получает бесконечно малое количество теплоты. Таких путей, а значит, и теплоёмкостей существует бесчисленное множество. Наиболее часто применяемые из них (но не единственно возмож-

ные) – теплоёмкости при постоянном объёме CV и постоянном давлении C p . Однако, как только тот или иной путь подвода тепла

фиксирован, теплоёмкость превращается из функции процесса в функцию состояния, что позволяет вычислять её с помощью част-

которого определяет путь подвода тепла, в частности, им может быть объём V или давление p.

8 Читается: dQ по dT при постоянном x.

78

Внутренняя энергия одного моля идеального газа может быть представлена в виде U 2i RT , где i – число степеней свободы мо-

лекул этого газа; R 8,31 Дж/моль·К – универсальная газовая постоянная. Если учесть, что в изохорическом процессе (V=const) газ работы не совершает ( A pdV 0 ), то, исходя из уравнения (I),

идеального газа зависит только от температуры, то последнюю частную производную можно заменить на обычную, и тогда молярная теплоёмкость при постоянном объёме определится как

Для того чтобы отыскать молярную теплоёмкость идеального газа для изобарического процесса (p=const), нужно использовать кроме первого начала термодинамики, уравнение состояния, которое в этом случае, как известно, имеет вид

где m и M – масса и молярная масса газа соответственно. Тогда для одного моля

Это уравнение впервые было получено Ю. Майером, немецким врачом и естествоиспытателем, и носит его имя. Майеру также принадлежит заслуга открытия первого начала термодинамики. Обратим внимание на то, что соотношение (IV) справедливо в таком виде только для молярных теплоёмкостей. С учётом (II) формулу (IV) можно также представить через число степеней свободы молекулы газа:

79

Одним из важнейших соотношений между теплоёмкостями C p и CV (не обязательно молярными) является их отношение, на-

зываемое коэффициентом Пуассона (γ):

степеней свободы молекулы, которое можно определить как число её возможных независимых движений. Поскольку материальная точка может совершать только поступательное движение вдоль трёх пространственных осей, присущее ей, а значит, и одноатомной молекуле число степеней свободы равно трём ( i = 3, = 5/3).

Для двухатомной молекулы добавляются ещё вращения вокруг двух взаимно перпендикулярных осей, проходящих через её центр инерции, но не совпадающих с линией, соединяющей центры атомов ( i = 5, = 1,4). Наконец, при трёх и более атомах в молекуле

только для жёстких, движущихся как целое, молекул, т.е. молекул, атомы которых не совершают колебаний.

Рассмотрим изменение состояния идеального газа при его адиабатическом расширении. Адиабатическим процессом называется процесс, протекающий без теплообмена с окружающей средой ( Q = 0). При этом первое начало термодинамики примет вид

pdV Mm 2i RdT .

Газ при адиабатическом расширении и сжатии совершает работу только за счёт своей внутренней энергии. Следовательно, при расширении он охлаждается, а при сжатии нагревается. Соотношение между давлением и объёмом идеального газа при адиабатическом процессе представляет уравнение Пуассона, или уравнение адиабаты:

80