3.3.2. Формула Ньютона – Лейбница.

1. Определённый интеграл с переменным верхним пределом.

Пусть в интеграле нижний предела = const, а верхний пределb изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.

Обозначим 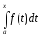= Ф(х) (3.3.10)

Найдем производную функции Ф(х) по переменному верхнему пределу х.

(3.3.11)

Интеграл (3.3.10) называется интегралом с переменным верхним пределом.

Аналогичное свойство существует и для случая переменного нижнего предела.

2. Теорема Ньютона – Лейбница.

Теорема 3.3.3.

Если функция F(x) – какая- либо первообразная от непрерывной функцииf(x), то(3.3.12)

Выражение (3.3.12) известно под названием формулы Ньютона – Лейбница.

Доказательство.

Пусть F(x) – первообразная функцииf(x). Тогда в соответствии с приведенной выше теоремой, функция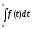- первообразная функция отf(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то

при соответствующем выборе С это равенство справедливо для любогох,т.е. прих = а:

, но, следовательно, т.е.

. Тогда.

А при х = b: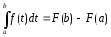

Заменив переменную tна переменную х, получаем формулу Ньютона – Лейбница:

Теорема доказана.

3.3.3. Методы интегрирования.

1. Замена переменных в определённом интеграле.

Пусть задан интеграл 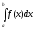, гдеf(x)– непрерывная функция на отрезке[a, b]. Введем новую переменную в соответствии с формулой

x = (t).Тогда если

1) () = а, () = b

2) (t) и (t)непрерывны на отрезке[, ]

3) f((t)) определена на отрезке [,],

то (3.3.13)

Тогда

Пример 1.

Пример 2.

, с другой стороны, если применить тригонометрическую подстановку,

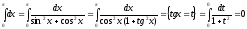
Т.е. два способа нахождения интеграла дают различные результаты. Это произошло из-за того, что не был учтен тот факт, что введенная переменная tgxимеет на отрезке интегрирования разрыв (в точкех = /2). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.

2. Интегрирование по частям.

Если функции u = (x)иv = (x)непрерывны на отрезке[a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:

(3.3.14)

Вывод этой формулы абсолютно аналогичен выводу формулы интегрирования по частям для неопределенного интеграла, который был весьма подробно рассмотрен выше, поэтому здесь приводить его нет смысла.

3. Приближенное вычисление определенного интеграла.

Существуют функции, интеграл от которых не может быть выражен через элементарные функции. Для нахождения интегралов от подобных функций применяются разнообразные приближенные методы.

1.Формула прямоугольников.

Пустьизвестны значения функцииf(x) в некоторых точкахx₀,x₁, … ,x_m:

y₀ = f(x₀), y₁ = f(x₁), …. , y_n = f(x_n).

Разобъём отрезок интегрирования наnравных частей.

Составим суммы: y₀x+y₁x+ … +y_n-1x

y₁x+y₂x+ … +y_nx

Это соответственно нижняя и верхняя интегральные суммы. Первая соответствует вписанной ломаной ограничивающей кривой, вторая – описанной. Тогда

=(3.3.15)

или

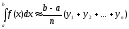(3.3.16)

Формулы (3.3.15) и (3.3.16) называются формулами прямоугольников.

2. Формула трапеций.

у

у_n

у₂

y₁

ax₁x₂bx

Пусть I = (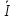+)т.е.

(3.3.17)

Формула (3.3.17) называется формулой трапеций:

Формула парабол

(формула Симпсона или квадратурная формула).

(Томас Симпсон (1710-1761)- английский математик)

Разделим отрезок интегрирования [a,b] на четное число отрезков (2m). Площадь криволинейной трапеции, ограниченной графиком функцииf(x) заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси Оу и проходящей через точки кривой, со значениямиf(x₀),f(x₁),f(x₂).

Для каждой пары отрезков построим такую параболу.

у

0 х₀х₁х₂х₃х₄х

Уравнения этих парабол имеют вид Ax²+Bx+C, где коэффициенты А, В, С могут быть легко найдены по трем точкам пересечения параболы с исходной кривой.

(1)

Обозначим .

Если принять х₀= -h,x₁= 0,x₂=h, то(2)

Тогда уравнения значений функции (1) имеют вид:

Cучетом этого:.

Отсюда уравнение (2) примет вид:

Тогда

Складывая эти выражения, получаем формулу Симпсона:

Чем больше взять число m, тем более точное значение интеграла будет получено.

Пример.Вычислить приближенное значение определенного интеграла

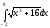с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей.

По формуле Симпсона получим:

m	0	1	2	3	4	5	6	7	8	9	10
x	-2	-1	0	1	2	3	4	5	6	7	8
f(x)	2.828	3.873	4	4.123	4.899	6.557	8.944	11.874	15.232	18.947	22.978

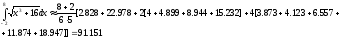
Точное значение этого интеграла – 91.173.

Как видно, даже при сравнительно большом шаге разбиения точность полученного результата вполне удовлетворительная.

Для сравнения применим к этой же задаче формулу трапеций.

Формула трапеций дала менее точный результат по сравнению с формулой Симпсона.

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая вычисляет любой определенный интеграл всеми рассмотренными выше методами.