
- •Лекция 1 Введение
- •Структура курса
- •Учебники
- •Задачники
- •Раздел 1. Алгебра и геометрия.
- •Тема 1.1. Определители.
- •Лекция 2.
- •Тема 1.2. Матрицы.
- •1.2.1.Понятие матрицы.
- •1.2.2.Операции с матрицами.
- •Лекция 3
- •Тема 1.3. Обратная матрица.
- •1.3.1.Понятие обратной матрицы.
- •Если матрица а имеет обратную матрицу а-1, то она единственная.
- •1.3.2. Получение обратной матрицы с помощью присоединенной матрицы.
- •1.3.3. Получение обратной матрицы методом элементарных преобразований.
- •Тема 1.4. Система линейных алгебраических уравнений (слау)
- •1.4.1.Решение слау методом Крамера.
- •1.4.2. Решение слау методом Гаусса
- •1.4.3 Решение слау с помощью обратной матрицы
- •Тема 1.5. Однородные, неопределённые и несовместные системы линейных алгебраических уравнений (слау)
- •1.5.1. Решение однородных слау.
- •1.5.2.Решение неопределённых слау.
- •1.5.3. Определение несовместных слау.
- •Лекция 6
- •1.6. Векторная алгебра
- •1.4.1. Вектор. Линейные операции с векторами. Базис. Декартова система координат (дск).
- •1.6.2. Скалярное, векторное и смешанное произведение векторов.
- •1.4.3 Преобразование координат. Полярная система
- •Переход из пск в дск и из дск в пск
- •Лекция 7
- •1.7 Аналитическая геометрия
- •1.7.1 Аналитическая геометрия на плоскости. Уравнение прямой линии на плоскости.
- •1.7.2 Кривые второго порядка в декартовой системе координат.
- •1.7.3. Кривые второго порядка в полярной системе координат.
- •Лекция 8
- •1.8 Аналитическая геометрия в пространстве.
- •1.8.1 . Уравнение плоскости в пространстве.
- •4) Условия параллельности и перпендикулярности плоскостей.
- •1.8.2. Уравнение прямой линии в пространстве.
- •1.8.3. Поверхности 2-го порядка.
- •Раздел 2. Дифференциальное исчисление.
- •Тема 2.1. Введение в анализ.
- •2.1.1. Действительные числа. Абсолютная величина действительного числа. Постоянные и переменные величины.
- •3) Свойства абсолютной величины.
- •2.1.3. Предел функции. Основные теоремы о пределах.
- •4) Основные теоремы о пределах.
- •Тема 2.2. Предел и непрерывность функции.
- •2.2.1. Первый и второй замечательные приделы. Раскрытие неопределённостей типа .
- •2.2.2. Непрерывность функции.
- •2.2.3. Бесконечно малые функции и бесконечно большие функции.
- •Тема 2.3. Производные функции одной переменной.
- •Тема 2.4. Дифференциал.
- •Тема 2.5. Основные теоремы о дифференцируемых функциях.
- •Тема 2.6. Некоторые сведения из высшей алгебры.
- •2.6.2. Теоремы Гаусса и Безу.
- •2.6.3. Разложение алгебраических многочленов на множители.
- •Модуль 3. Интегральное исчисление.
- •Тема 3.1. Неопределенный интеграл.
- •3.1.1. Первообразная и неопределенный интеграл.
- •3.1.2. Свойства неопределенного интеграла и таблица интегралов.
- •3.1.3. Методы интегрирования
- •Тема 3.2. Интегрирование рациональных и тригонометрических функций.
- •3.2.1. Интегрирование рациональных дробей.
- •3.2.2. Интегрирование иррациональных функций.
- •3.2.3. Интегрирование тригонометрических функций.
- •Тема 3.3. Определенный интеграл.
- •3.3.1. Определенный интеграл. Теорема существования. Основные свойства определенного интеграла.
- •3.3.2. Формула Ньютона – Лейбница.
2.2.3. Бесконечно малые функции и бесконечно большие функции.
1) Основные понятия.
Функция
x
называется бесконечно малой функцией
при х
а, (x∞)
, если
 ,
, .
.
Функция
x
называется бесконечно большой функцией
при х
а, (x∞)
, если
 ,
, .
.
Функция, обратная бесконечно малой, есть функция бесконечно большая.
2) Основные теоремы.
1)) Сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
2)) Произведение бесконечно малой функции на функцию ограниченную есть бесконечно малая функция.
3))
Если функция у
= у(х)
может быть представлена в виде у
= b
+ ,
где b
=
const,
а
= (x)
– бесконечно малая функция при х
а
,
то
 .
.
3) Сравнение бесконечно малых функций.
Если
 ,
где(х)
и
(х)
– бесконечно малые функции при х
а,
то
и
называются бесконечно малыми функциями
одного порядка малости.
,
где(х)
и
(х)
– бесконечно малые функции при х
а,
то
и
называются бесконечно малыми функциями
одного порядка малости.
Если
 ,
то
называется
бесконечно малой функцией (б.м.ф.) большого
порядка малости чем
,
то
называется
бесконечно малой функцией (б.м.ф.) большого
порядка малости чем
Если
 ,
то
- называется б.м.ф. меньшего порядка
малости чем .
,
то
- называется б.м.ф. меньшего порядка
малости чем .
Если
 ,
то бесконечно малые функции
и
называются эквивалентами б.м.ф.
,
то бесконечно малые функции
и
называются эквивалентами б.м.ф.
Если и - эквивалентные бесконечно малые функции, то () - б.м.ф. большего порядка малости, чем и чем .
Типовые примеры.
1.
Решение.

2.

Решение.


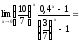
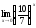

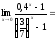
 =
=
Лекция 11.
Тема 2.3. Производные функции одной переменной.
Производная и ее геометрический смысл.
Производные основных элементарных функций.
Производные сложных и обратных функций и функций заданных параметрически.
Производная и ее геометрический смысл.
Понятие производной.
Производной
функции f(x)
в точке х = х0
называется предел отношения приращения
функции в этой точке к приращению
аргумента, если он существует
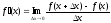 .
.
Если
у
= у(х),
то
 =
= (2.3.1.)
(2.3.1.)
Геометрическая интерпретация производной.
у f(x)
f(x0 +x) P
f
f(x0) M
x
0 x0 x0 + x x
Пусть
f(x)
определена на некотором промежутке (a,
b).
Тогда
 тангенс угла наклона секущей МР к графику
функции.
тангенс угла наклона секущей МР к графику
функции.
 ,
,
где - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Производная
 равна тангенсу угла наклона касательной
к графику функцииy=у(х)в точкехк оси 0х:
равна тангенсу угла наклона касательной
к графику функцииy=у(х)в точкехк оси 0х:
 =tg .
(2.3.2.)
=tg .
(2.3.2.)
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
Уравнение
касательной к кривой:

Уравнение
нормали к кривой:
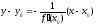 .
.
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.
Связь непрерывности с дифференцируемостью.
Если функция у = у(х)имеет в точкех производную, то она называется дифференцируемой в точкех.
Если функция у = у(х)дифференцируема в точкех,то она в этой точке непрерывна. Обратное утверждение неверно, т.е. из непрерывности дифференцируемость не следует.
Основные правила дифференцирования.
 =
0, (2.3.3)
=
0, (2.3.3)
 ,(2.3.4)
,(2.3.4)
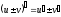 ,(2.3.5)
,(2.3.5)
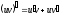 ,
(2.3.6)
,
(2.3.6)
 ,
(2.3.7)
,
(2.3.7)
Производные основных элементарных функций.
 =
n x n-1 (2.3.8)
=
n x n-1 (2.3.8)
 =
ax
ln a (2.3.9)
=
ax
ln a (2.3.9)
 =
= (2.3.10)
(2.3.10)
(sin x)’ = cos x (2.3.11)
(cos x)’ = - sin x (2.3.12)
(tg x)’ =
 (2.3.13)
(2.3.13)
(ctg x)’ = - (2.3.14) (arc
sin x)’ =
(2.3.14) (arc
sin x)’ =
 (2.3.15)
(2.3.15)
(arc cos x) = -
 (2.3.16) (arc tg x) =
(2.3.16) (arc tg x) =
 (2.3.17)
(2.3.17)
(arc ctg
x) = -
 (2.3.18)
(2.3.18)
Типовой пример.
Доказать, что
 =
a x
ln a.
=
a x
ln a.
Доказательство.

Таблица производных
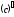 =
0 14. (ctg
x)’ = -
=
0 14. (ctg
x)’ = - 27.
27.

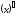 =1
15. (sh x)’ = ch x
28.
=1
15. (sh x)’ = ch x
28.

 16. (ch x)’ = sh x
29.
16. (ch x)’ = sh x
29.

 =
n x n-1
17.
(th x)’ =
=
n x n-1
17.
(th x)’ =
 30.
30.
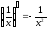 18. (cth x)’ = -
18. (cth x)’ = -
 31.
31.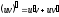
 19. (arc sin x)’ =
19. (arc sin x)’ =
 32.
32.
 =
a x
ln a 20. (arc cos x) = -
=
a x
ln a 20. (arc cos x) = -
 33.
33.

 21. (arc tg x) =
21. (arc tg x) =
 34.
34.
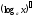 =
=
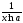 22. (arc ctg x) = -
22. (arc ctg x) = - 35.
35.
 23.
23.
 36.
36.
(sin x)’ = cos x 24.
 37.
37.
(cos x)’ = - sin x 25.
 38.
38.
13.(tg x)’
=
 26.
26.
Формулы Эйлера
1.
 .
2.
.
2. .
3.
.
3. .
4.
.
4. .
.
5.
 .
6.
.
6. .
7.
.
7. .
8.
.
8. .
.
9.
Производные сложных и обратных функций и функций заданных параметрически.
1) Производные сложных функций
 (2.3.19)
(2.3.19)
Теорема 2.3.1.
Пусть
y
= f(u);
u
= g(x),
причем область значений функции u
входит в область определения функции
f. Тогда

Доказательство.


(
с учетом того, что если x0,
то u0,
т.к. u
= g(x)
– непрерывная функция). Тогда

Теорема доказана.
Производная сложной показательной функции
 (2.3.20)
(2.3.20)
Найдем производную функции y = uv. Логарифмируя, получим:
lny = vlnu

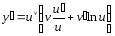

Производные обратных функций
 (2.3.21)
(2.3.21)
3) Производные функций заданных параметрически
 (2.3.22)
(2.3.22)
 (2.3.33)
(2.3.33)
Лекция 12
