
Geom / AnGeom_2
.pdf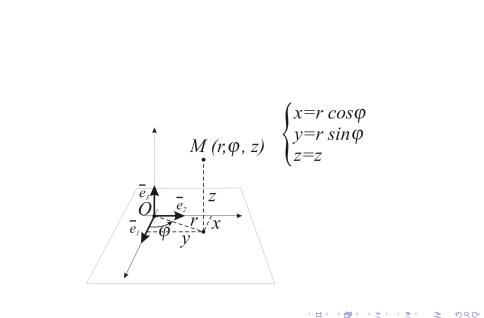
Системы координат Координаты вектора
Системы координат на плоскости
Линейная зависимость и независимость векторов
Системы координат в пространстве
Цилиндрическая система координат в пространстве
Ассоциированная прямоугольная система координат.
Аналитическая геометрия. Лекция 2

Системы координат Координаты вектора
Системы координат на плоскости
Линейная зависимость и независимость векторов
Системы координат в пространстве
Сферическая система координат в пространстве
Плоскость с фиксированной на ней полярной системой
координат ( , −→, направление), вектор, перпендикулярный
O e1
плоскости, длина которого равна длине вектора −→. e1
Аналитическая геометрия. Лекция 2

Системы координат Координаты вектора
Системы координат на плоскости
Линейная зависимость и независимость векторов
Системы координат в пространстве
Сферическая система координат в пространстве
Ассоциированная прямоугольная система координат.
Аналитическая геометрия. Лекция 2

Системы координат Координаты вектора Линейная зависимость и независимость векторов
Определение.
Пусть в прямоугольной системе координат |
{ |
→− →− →− |
} |
|
|
O, e1 , e2 e3 |
|
||
→− |
→− →− →− |
→− |
|
|
вектор v |
представим в виде v = αe1 + βe2 |
+ γe3 . Тогда |
||
{ } −→
набор чисел α, β, γ называется координатами вектора v в данной системе координат.
Аналитическая геометрия. Лекция 2

Системы координат Координаты вектора Линейная зависимость и независимость векторов
Сложение векторов, заданных своими координатами.
Пусть в прямоугольной (аффинной) системе координат |
|||||||||||||||||||||||
|
|
a |
|
→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
векторы →− |
и |
|
b |
заданы своими координатами |
|
|
|||||||||||||||||
|
|
} |
|
|
|||||||||||||||||||
|
{ |
|
|
|
|
|
b = |
{ |
x , y , z |
} |
|
|
|
|
|
|
|
|
|||||
a |
= x , y |
, z |
1 |
|
, |
→− |
|
2 |
2 2 |
|
|
. Тогда |
|
|
|
|
|
||||||
→− |
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
a + →− |
{ |
|
|
|
|
|
|
|
|
|
|
|
|
} |
|
||||
|
|
|
→− |
|
|
b = |
x |
1 |
+ x |
, y |
1 |
+ y |
, z |
1 |
+ z |
2 |
. |
||||||
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
||||||||
Умножение на число вектора, заданного своими координатами.
Пусть в прямоугольной (аффинной) системе координат
вектор →− задан своими координатами →− { 1 1 1}. a a = x , y , z
Тогда для любого числа α
α→− |
= |
{ |
1 1 1 |
} |
|
|
a |
αx , αy , αz |
. |
||||
|
|
Аналитическая геометрия. Лекция 2

Системы координат Координаты вектора Линейная зависимость и независимость векторов
Сложение векторов, заданных своими координатами.
Пусть в прямоугольной (аффинной) системе координат |
|||||||||||||||||||||||
|
|
a |
|
→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
векторы →− |
и |
|
b |
заданы своими координатами |
|
|
|||||||||||||||||
|
|
} |
|
|
|||||||||||||||||||
|
{ |
|
|
|
|
|
b = |
{ |
x , y , z |
} |
|
|
|
|
|
|
|
|
|||||
a |
= x , y |
, z |
1 |
|
, |
→− |
|
2 |
2 2 |
|
|
. Тогда |
|
|
|
|
|
||||||
→− |
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
a + →− |
{ |
|
|
|
|
|
|
|
|
|
|
|
|
} |
|
||||
|
|
|
→− |
|
|
b = |
x |
1 |
+ x |
, y |
1 |
+ y |
, z |
1 |
+ z |
2 |
. |
||||||
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
||||||||
Умножение на число вектора, заданного своими координатами.
Пусть в прямоугольной (аффинной) системе координат
вектор →− задан своими координатами →− { 1 1 1}. a a = x , y , z
Тогда для любого числа α
α→− |
= |
{ |
1 1 1 |
} |
|
|
a |
αx , αy , αz |
. |
||||
|
|
Аналитическая геометрия. Лекция 2

Системы координат Координаты вектора
Определение
Линейная зависимость и независимость векторов
Свойства линейной независимости
Определение.
|
|
|
|
a |
, |
a |
|
, . . . |
|
a |
|
|
|
Линейной комбинацией векторов →− 1 |
→− 2 |
|
|
, →− n |
|
, |
|||||||
a |
|
+ α |
|
a |
|
+ |
· · · |
+ α |
a |
α |
|||
называется выражение α1→− |
1 |
|
2 |
→− 2 |
|
|
|
|
|
n→− n, где |
1 |
||
α2, . . . , αn некоторые числа.
Определение.
a |
1, |
a |
|
, . . . |
a |
называются линейно |
|
|
|
||||||
Векторы →− |
→− |
2 |
|
, →− n |
|
0 |
|
||||||||
независимыми, если |
α a |
|
+ α |
a |
+ |
· · · |
+ α |
a |
= |
→− |
, |
||||
1→− |
1 |
|
2→− 2 |
|
|
n→− n |
|
|
|||||||
тогда и только тогда, когда α1 = 0, α2 = 0, . . . , αn = 0.
Аналитическая геометрия. Лекция 2

Системы координат Координаты вектора
Определение
Линейная зависимость и независимость векторов
Свойства линейной независимости
Определение.
|
|
|
|
a |
, |
a |
|
, . . . |
|
a |
|
|
|
Линейной комбинацией векторов →− 1 |
→− 2 |
|
|
, →− n |
|
, |
|||||||
a |
|
+ α |
|
a |
|
+ |
· · · |
+ α |
a |
α |
|||
называется выражение α1→− |
1 |
|
2 |
→− 2 |
|
|
|
|
|
n→− n, где |
1 |
||
α2, . . . , αn некоторые числа.
Определение.
a |
1, |
a |
|
, . . . |
a |
называются линейно |
|
|
|
||||||
Векторы →− |
→− |
2 |
|
, →− n |
|
0 |
|
||||||||
независимыми, если |
α a |
|
+ α |
a |
+ |
· · · |
+ α |
a |
= |
→− |
, |
||||
1→− |
1 |
|
2→− 2 |
|
|
n→− n |
|
|
|||||||
тогда и только тогда, когда α1 = 0, α2 = 0, . . . , αn = 0.
Аналитическая геометрия. Лекция 2

Системы координат Координаты вектора
Определение
Линейная зависимость и независимость векторов
Свойства линейной независимости
Определение.
→− →− →−
Векторы a 1, a 2, . . . , a n называются линейно зависимыми, если существует набор α1, α2, . . . , αn чисел не все равные
|
α |
a |
|
+ α |
a |
|
+ + α a |
= |
0 |
|
|
нулю, при котором |
1 |
2 |
→− |
. |
|||||||
|
1→− |
|
2→− |
· · · |
n→− n |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Пример.
a |
= {1, 2, 3}, |
a |
= |
{ |
0, |
− |
1, 2 |
a |
= |
{ |
1, 1, 5 |
}. |
→− 1 |
→− 2 |
|
|
|
}, →− 3 |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
Вектор {→− 1} является линейно независимым, так как в |
||||||||||||
|
|
|
|
|
|
6 |
|
|
|
|
0 |
|
противном случае нашлось бы |
α |
|
= 0 |
α |
|
a |
= →− |
, т.е. |
||||
|
1 |
|
, что |
|
1 |
→− 1 |
|
|||||
a |
= →− |
|
|
|
|
|
|
|
|
|
|
|
→− 1 |
0 |
, что не верно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
a |
, a |
|
|
|
|
|
|
|
|
|
Векторы {→− 1 |
→− 2} является линейно независимым, так как |
|||||||||||
иначе нашлись бы α1 и α2 одновременно не равные 0, что
α |
|
a |
|
+ α |
|
a |
|
= |
0 |
|
α |
a |
|
= α |
a |
|
1 |
1 |
2 |
2 |
→− |
, т.е. |
1 |
→− |
1 |
− 2 |
→− |
2, что не верно, так |
|||||
|
→− |
|
→− |
|
|
как координаты векторов не пропорциональны.
Аналитическая геометрия. Лекция 2

Системы координат Координаты вектора
Определение
Линейная зависимость и независимость векторов
Свойства линейной независимости
Определение.
→− →− →−
Векторы a 1, a 2, . . . , a n называются линейно зависимыми, если существует набор α1, α2, . . . , αn чисел не все равные
|
α |
a |
|
+ α |
a |
|
+ + α a |
= |
0 |
|
|
нулю, при котором |
1 |
2 |
→− |
. |
|||||||
|
1→− |
|
2→− |
· · · |
n→− n |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Пример.
a |
= {1, 2, 3}, |
a |
= |
{ |
0, |
− |
1, 2 |
a |
= |
{ |
1, 1, 5 |
}. |
→− 1 |
→− 2 |
|
|
|
}, →− 3 |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
Вектор {→− 1} является линейно независимым, так как в |
||||||||||||
|
|
|
|
|
|
6 |
|
|
|
|
0 |
|
противном случае нашлось бы |
α |
|
= 0 |
α |
|
a |
= →− |
, т.е. |
||||
|
1 |
|
, что |
|
1 |
→− 1 |
|
|||||
a |
= →− |
|
|
|
|
|
|
|
|
|
|
|
→− 1 |
0 |
, что не верно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
a |
, a |
|
|
|
|
|
|
|
|
|
Векторы {→− 1 |
→− 2} является линейно независимым, так как |
|||||||||||
иначе нашлись бы α1 и α2 одновременно не равные 0, что
α |
|
a |
|
+ α |
|
a |
|
= |
0 |
|
α |
a |
|
= α |
a |
|
1 |
1 |
2 |
2 |
→− |
, т.е. |
1 |
→− |
1 |
− 2 |
→− |
2, что не верно, так |
|||||
|
→− |
|
→− |
|
|
как координаты векторов не пропорциональны.
Аналитическая геометрия. Лекция 2
