
Geom / AnGeom_2_12
.pdf
Прямолинейные образующие гиперболического параболоида Поверхности вращения
Приведение к каноническому виду
Аналитическая геометрия
Лекция 27. Поверхности второго порядка
Сбродова Елена Александровна
27 апреля 2012 г.
Аналитическая геометрия. Лекция 27

Прямолинейные образующие гиперболического параболоида Поверхности вращения
Приведение к каноническому виду
Прямолинейные образующие гиперболического параболоида
Теорема о прямолинейных образующих гиперболического параболоида.
Пусть гиперболический параболоид задан каноническим
|
|
|
x2 |
|
y2 |
|
|
|
|
||
уравнением 2z = |
|
− |
|
. Тогда |
|
|
|
|
|||
a2 |
b2 |
|
|
|
|
||||||
1. Прямые вида |
|
|
|
|
|
|
|
|
|||
|
α(xa |
yb ) = 2β |
6 |
|
α(xa |
yb ) = βz |
6 |
||||
β( a |
+ b ) = αz |
β( a |
+ b ) = 2α |
||||||||
(I) |
x |
− y |
|
α = 0; (II) |
|
x |
− y |
β = 0 , |
|||
целиком лежат на гиперболическом параболоиде.
Аналитическая геометрия. Лекция 27

Прямолинейные образующие гиперболического параболоида Поверхности вращения
Приведение к каноническому виду
Прямолинейные образующие гиперболического параболоида
2.Через каждую точку гиперболического параболоида проходят одна прямая вида (I) и одна прямая вида (II).
3.Семейство прямых вида (I) различны (II).
4.Любая прямая, лежащая на гиперболическом параболоиде, относится либо к семейству (I), либо к семейству (II).
Аналитическая геометрия. Лекция 27

Прямолинейные образующие гиперболического параболоида Поверхности вращения
Приведение к каноническому виду
Прямолинейные образующие гиперболического параболоида
Пример.
Пусть гиперболический параболоид задан каноническим
уравнением 2z = x2 − y2 . Найти прямолинейные
25 36
образующие, проходящие через точку (5, 6, 0).
Аналитическая геометрия. Лекция 27

Прямолинейные образующие гиперболического параболоида Поверхности вращения
Приведение к каноническому виду
Поверхности вращения
Определение.
Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости, называется
поверхностью вращения.
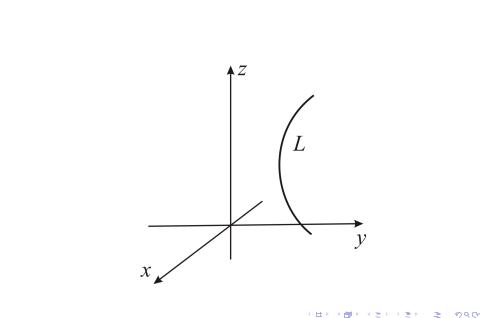
Пусть некоторая кривая L лежит в плоскости yOz.
F (y, z) = 0, x = 0.
Аналитическая геометрия. Лекция 27
Прямолинейные образующие гиперболического параболоида Поверхности вращения
Приведение к каноническому виду
Поверхности вращения
Аналитическая геометрия. Лекция 27
Прямолинейные образующие гиперболического параболоида Поверхности вращения
Приведение к каноническому виду
Поверхности вращения
Аналитическая геометрия. Лекция 27

Прямолинейные образующие гиперболического параболоида Поверхности вращения
Приведение к каноническому виду
Поверхности вращения
Уравнение поверхности вращения.
F (y, z) = 0 |
|
Дана кривая L: x = 0 |
в плоскости yOz. При |
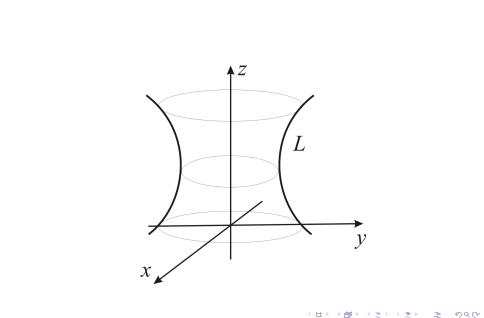
вращении L вокруг оси Oz, каждая точка M(0, y0, z0) кривой опишет окружность в плоскости z = z0. Все точки N(x, y, z0) этой окружности лежат на поверхности вращения.
• N(x, y, z0) окружности x2 + y2 + z02 = y02 + z02 или
p
± x2 + y2 = y0.
•M(0, y0, z0) L F (y0, z0) = 0.
•Т.о. поверхность вращения задается уравнением
p
F (± x2 + y2, z) = 0.
Аналитическая геометрия. Лекция 27

Прямолинейные образующие гиперболического параболоида Поверхности вращения
Приведение к каноническому виду
Поверхности вращения
Уравнение поверхности вращения.
F (y, z) = 0 |
|
Дана кривая L: x = 0 |
в плоскости yOz. При |
вращении L вокруг оси Oz, каждая точка M(0, y0, z0) кривой опишет окружность в плоскости z = z0. Все точки N(x, y, z0) этой окружности лежат на поверхности вращения.
• N(x, y, z0) окружности x2 + y2 + z02 = y02 + z02 или
p
± x2 + y2 = y0.
•M(0, y0, z0) L F (y0, z0) = 0.
•Т.о. поверхность вращения задается уравнением
p
F (± x2 + y2, z) = 0.
Аналитическая геометрия. Лекция 27

Прямолинейные образующие гиперболического параболоида Поверхности вращения
Приведение к каноническому виду
Поверхности вращения
Уравнение поверхности вращения.
F (y, z) = 0 |
|
Дана кривая L: x = 0 |
в плоскости yOz. При |
вращении L вокруг оси Oz, каждая точка M(0, y0, z0) кривой опишет окружность в плоскости z = z0. Все точки N(x, y, z0) этой окружности лежат на поверхности вращения.
• N(x, y, z0) окружности x2 + y2 + z02 = y02 + z02 или
p
± x2 + y2 = y0.
•M(0, y0, z0) L F (y0, z0) = 0.
•Т.о. поверхность вращения задается уравнением
p
F (± x2 + y2, z) = 0.
Аналитическая геометрия. Лекция 27
