63. Моделі ковзного середнього (ma(q)- процеси).

Стохастичний процес називають процесом ковзної середньої порядку , якщо до загальної моделі (2.1.1) входять лише складових. Позначимо коефіцієнти обмеженого ряду MA() літерою b, тоді модель ковзної середньої порядку має вигляд:

, (2.2.1)

де випадкова величина - білий шум, — лінійний оператор, та () невідомих параметрів треба оцінити на підставі вибіркових спостережень.

Процес (2.2.1) - стаціонарний, оскільки є окремим випадком загальної лінійної моделі, а саме, включно до j = q дорівнюють , решта дорівнюють нулю.

Операторний багаточлен можна розкласти на множники, використовуючи корені рівняння . Отже, лінійний оператор можна записати у вигляді:

,

де - корені рівняння .

- процес, відповідно, має вигляд:

.

За умови оберненості кожен скінченний MA()-процес може бути представлений у вигляді нескінченного авторегресійного процесу:

Автоковаріація та дисперсія MA() процесу відповідно дорівнюють:

.

.

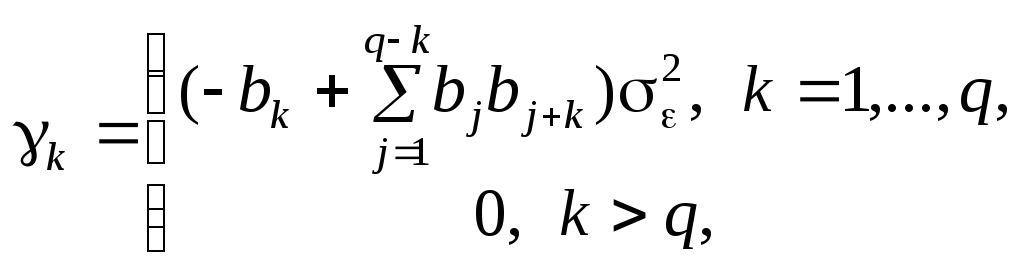Автокореляційна функція процесу має вигляд

, для .

Автокореляційну функцію використовують для визначення порядку MA()-процесу.

64. Авторегресійні моделі ковзного середнього ( arma(p,q)- процеси).

ARMA-процес є сумою AR та MA-процесів.

Заг. вигляд ARMA(p,q)-процесу:

y_t = c + Sum(φ_iy_t-i, i=1,p) + ε_t + Sum(θ_iε_t-i,i=1,q).

ARMA(p,q)-процес є стаціонарним, якщо всі корені z_i р-ня

1 - φ₁z - φ₂z²-…- φpzp = 0

задовольняють умові |z_i|>1.

ARMA(p,q)-процес є зворотним (тобто його можна перетворити у AR(∞)-процес або MA(∞)-процес), коли всі корені z_i р-ня

1 + θ₁z + θ₂z² +…+ θpzp = 0

задов. умові |z_i|>1.

65. Інтегровані авторегресійні моделі ковзного середнього ( arima(p,d,q)- процеси).

Розглянемо модель

, (2.4.6)

де, — нестаціонарний оператор авторегресії порядку ; оператор ковзної середньої . Тоді можна записати, що

,

де - стаціонарний порядку оператор авторегресії. Якщо ввести оператор різ­ниці ; , тоді запишеться як , і модель (2.4.6) можна представити у вигляді:

. (2.4.8)

Тут d-ту різницю ряду обчислюють за формулою:

. (2.4.9)

Вона задовольняє рівняння

,

тобто вже є стаціонарним оберненим процесом . З іншого боку, якщо ввести обернений до оператор:

,

який називають оператором підсумку (), то з (2.4.9) виходить, що

,

де під d-кратною ітерацією оператора S розуміють ряд

.

Отже, , що описується рівнянням (2.4.8), можна отримати d-кратним підсумком процесу , який є ARІMA. Тому процес, що задається моделлю (2.4.8), називають процесом ARІMA. Якщо в (2.4.8) оператор авторегресії має порядок , а оператор ковзної середньої має порядок , то скорочено модель (2.4.8) записують як ARІMA(p, d, q). Модель ARІMA охоплює широкий клас як стаціонарних (при ), так і нестаціонарних (при ) процесів. На практиці d є додатним цілим, яке не перевищує 2, або нулем у разі стаціонарності .

66. Адаптивні моделі. Схема їх побудови.

Адаптивне прогнозування дає змогу автоматично змінювати константу згладжування в процесі обчислення. Інструментом прогнозування в адаптивних методах є математична модель з одним чинником «час».

Адаптивні моделі прогнозування — це моделі дисконтування даних, які здатні швидко пристосовувати свою структуру й параметри до зміни умов. Найважливіша особливість їх полягає у тому, що це саморегулювальні моделі, й у разі появи нових даних прогнози оновлюються із мінімальною затримкою без повторення спочатку всього обсягу обчислень.Адаптивні моделі і методи мають механізм автоматичного налаштування на зміну досліджуваного показника. Інструментом прогнозу є модель, первинна оцінка параметрів якої проводиться за декількома першими спостереженнями. На її основі робиться прогноз, який порівнюється з фактичними спостереженнями. Далі модель корегується відповідно до величини помилки прогнозу і знов використовується для прогнозування наступного рівня, аж до вичерпання всіх спостережень. Таким чином, модель постійно "вбирає" нову інформацію, пристосовується до неї і до кінця періоду спостереження відображає тенденцію, що склалася на даний момент. Прогноз виходить як екстраполяція останньої тенденції. У різних методах прогнозування процес налаштування (адаптації) моделі здійснюється по-різному. Базовими адаптивними моделями є: Модель Брауна; Модель Хольта; Модель авторегресії.

Перші дві моделі відносяться до схеми ковзаючого середнього, остання - до схеми авторегресії. Численні адаптивні методи ґрунтуються на цих моделях і розрізняються між собою способом числової оцінки параметрів, визначення параметрів адаптації і компонуванням.

Згідно із схемою ковзаючого середнього, оцінкою поточного рівня є зважене середнє всіх попередніх рівнів, причому ваги при спостереженнях зменшуються в міру віддалення від останнього (поточного) рівня, тобто інформаційна цінність спостережень тим більша, чим ближче вони до кінця періоду спостережень.

Згідно із схемою авторегресії, оцінкою поточного рівня є зважена сума "p" попередніх рівнів (їх кількість називається порядком моделі). Інформаційна цінність спостережень визначається не їх близькістю до модельованого рівня, а тіснотою зв'язку між ними.

Обидві схеми мають механізм відображення коливального (сезонного або циклічного) розвитку досліджуваного процесу.