52. Поняття часового лагу. Моделі з часовим лагом незалежних змінних.

Для багатьох економічних процесів типовим є те, що ефект від впливу деякого фактора на показник, який характеризує процес, виявляється не одразу, а поступово, через деякий період часу. Таке явище називається лагом (запізненням).

Потреба враховувати лаг під час кількісного вимірювання взаємозв’язку між економічними показниками постає дуже часто. Наприклад, у динамічних моделях необхідно враховувати лаг при визначенні зв’язку між обсягом продукції і капітальними вкладеннями, або частину цього лагу — будівельний.

Нехай економетрична модель розподіленого лагу визначається так:

де - параметри моделі при лагових змінних; - пояснювальна лагова змінна;  - період зрушення; - залишки, що розподілені нормально, тобто мають нульове математичне сподівання і сталу дисперсію.

Модель називається загальною моделлю нескінченного розподіленого лагу, якщо для неї справджуються такі умови:

1) , для будь-яких k, j;

2) , j = 1, 2, 3...; k = 1, 2, 3...;

3) , де w — певне число;

4) ;

5) , .

53. Авторегресійні моделі.

Авторегресійна модель має вигляд:

Ідентифікація порядку d різницевого ряду zt, t = 1,...,n’ = n – d виконується за допомогою тих самих засобів, що й для несезонних моделей. Порядок AR (p)-моделі можна обрати такий, що дорівнюватиме періоду сезонності, тобто р = т. У цьому разі її розмірність збігається із розмірністю моделі Вінтерса, параметри моделі набувають змісту індексів сезонності, але визначаються в інший спосіб (МНК). Кількість параметрів можна скоротити за рахунок несуттєвих за величиною впливу коефіцієнтів.

54. Оцінювання авторегресійних моделей з часовим лагом незалежних змінних.

Один із способів звільнитися від мультиколінеарності - це ввести такі коефіцієнти при лагових змінних, які мали б однаковий знак і для них можна було знайти суму. З урахуванням умов модель з розподіленим лагом набере такого вигляду:

Л. Койк запропонував вибрати для запису вагових коефіцієнтів форму спадної геометричної прогресії

(10.11)

Звідси

(10.12)

Якщо через D позначити оператор зрушення такий, що Dx_t = x_t–1, D²x_t = x_t–2 і т. д., то вираз (10.11) можна записати так:

.

З урахуванням цього модель (10.12) матиме вигляд:

Для геометричного розподілу середній лаг

Входження до формули (10.12) лагового значення змінної Y може забезпечити досить добру апроксимацію моделі.

Розглянемо ще один підхід до розв’язування задачі вибору ваги для коефіцієнтів моделей при лагових пояснювальних змінних, який був запропонований Ширлі Алмон [2].

Нехай економетрична модель розподіленого лагу запишеться так:

(10.15)

Це означає, що пояснювальна змінна впливатиме на протягом  періодів. Аби скористатися схемою вибору , необхідно визначити величину . У попередньому розділі ми показали, як це можна зробити, скориставшись взаємною кореляційною функцією.

За теоремою Веєрштрасса значення параметрів моделі апроксимують за допомогою деякої функції , яка запишеться у вигляді многочлена від z:

Узявши s = 3 і а = 6, дістанемо таку схему для оцінювання параметрів моделі розподіленого лагу:

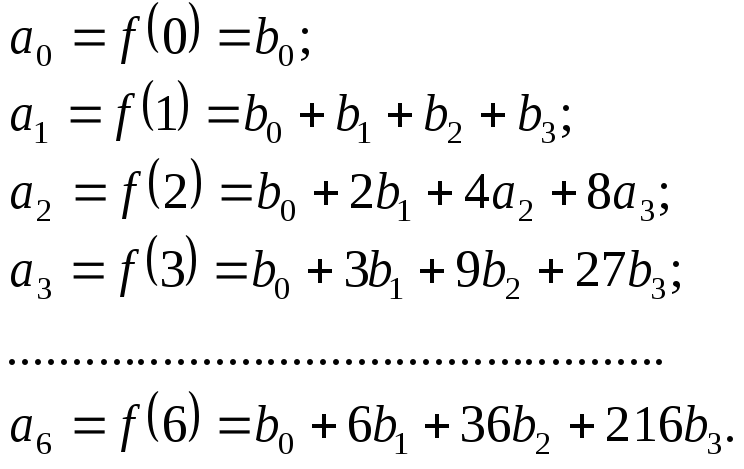(10.16)

Це означає, що кожну з оцінок параметрів моделі розподіленого лагу подано через чотири невідомі параметри многочлена: .

Підставивши оцінку з (10.16) в модель (10.15), дістанемо:

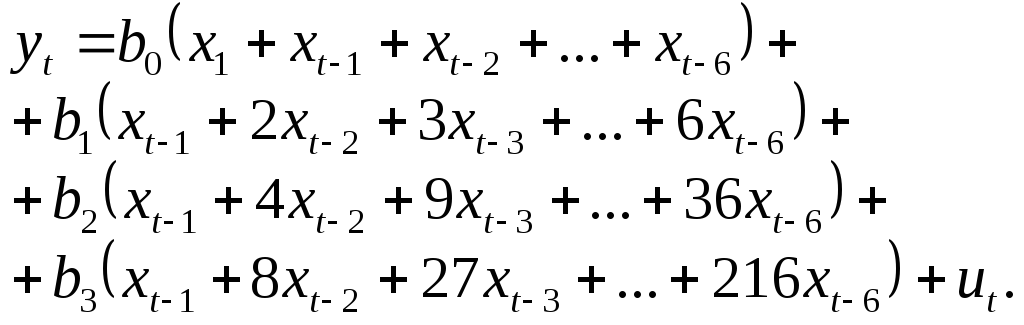
55. Автокореляція часового ряду, коефіцієнт автокореляці, автокореляційна функція.

    Коефіцієнт автокореляції між зрушеними на рівнями часового ряду - це автоковаріація, розділена на корінь із добутку двох дисперсій, та оскільки дисперсія стала, отримуємо прост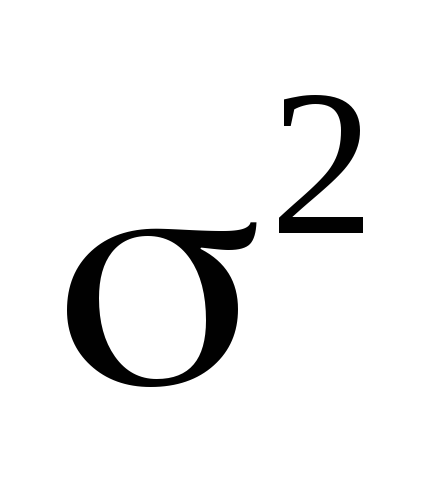о або 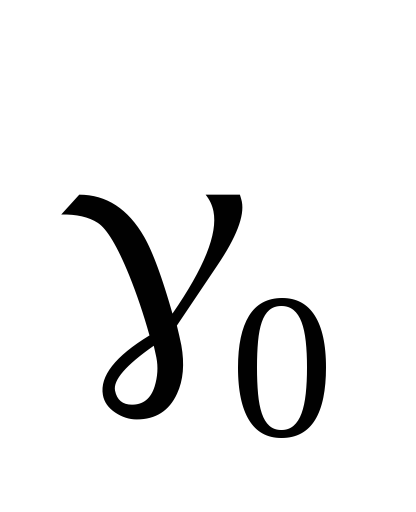. Розраховують коефіцієнт автокореляції за формулою:

. (1.2.8)

Вираз (1.2.8) визначає автокореляційну функцію (АКФ) часового ряду, яка показує наскільки статистично залежними є значення часового ряду для різних зрушень у часі (наприклад, для річних спостережень рік чи два роки тощо). Автокореляційна функція стаціонарного часового ряду залежить лише від різниці між двома моментами часу , і є парною функцією, тобто . Задаючи різні значення = 1, 2, 3,..., отримують послідовність значень , , ,... Графік автокореляційної функції називають корелограмою. За корелограмою можна визначити запізнення, із яким зміна показника позначається на його наступних значеннях.