39. Тест Гольдфельда-Квандта. Послідовність його виконання.

коли сукупність спостережень невелика, Гольдфельд і Квандт склали параметричний тест, в якому потрібно виконати такі кроки.

Крок 1. Упорядкувати спостереження відповідно до величини елементів вектора X_j.

Крок 2. Відкинути c спостережень, які містяться в центрі вектора. Згідно з експериментальними розрахунками автори знайшли оптимальні співвідношення між параметрами c і n для 30—60 спостережень, де n — кількість елементів вектора : .

Крок 3. Побудувати дві економетричні моделі на основі 1МНК за двома утвореними сукупностями спостережень обсягом ,

Крок 4. Знайти суму квадратів залишків за першою і другою моделями і :

,де — залишки за моделлю (1);

,де — залишки за моделлю (2).

Крок 5. Обчислити критерій

, який у разі виконання гіпотези про гомоскедастичність відповідатиме F-розподілу з , ступенями свободи. Це означає, що обчислене значення R^* порівнюється з табличним значенням F-критерію для ступенів свободи і і вибраним рівнем значущості . Якщо , то гетероскедастичність відсутня.

40. Алгоритм теста Глейсера.

Глейзер. розглядає регресію модуля залишків , що відповідають регресії найменших квадратів, як певну функцію від , де — та незалежна змінна, яка відповідає зміні дисперсії . Для цього використовуються такі види функцій:

1) ; 2) ;

3) 4) .

У цих рівняннях — стохастична складова.

Рішення про відсутність гетероскедастичності залишків приймається на підставі статистичної значущості коефіцієнтів і Переваги цього тесту визначаються можливістю розрізняти випадок чистої і мішаної гетероскедастичності.

Можливі чотири випадки:

1. є статистично значущими;

2. — статистично значуща, — статистично незначуща оцінка;

3. — статистично значуща, — статистично незначуща оцінка;

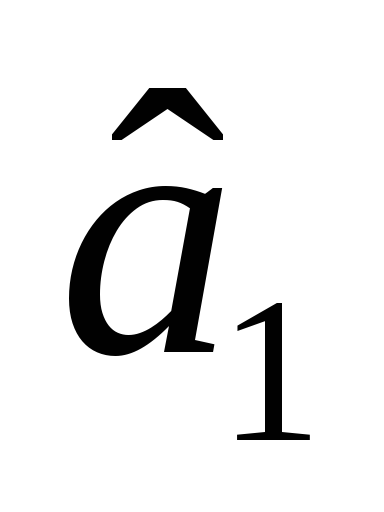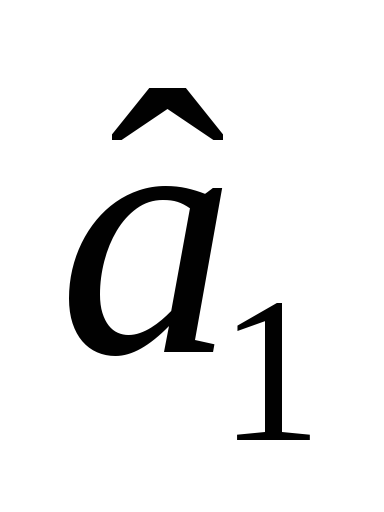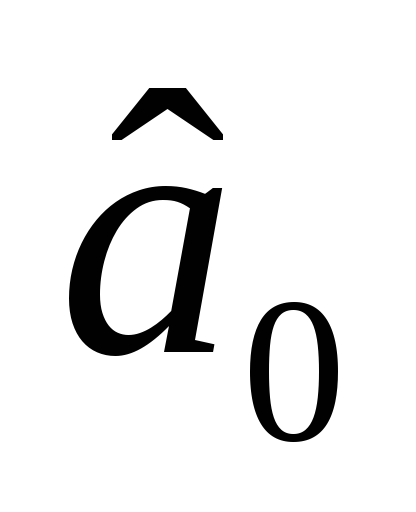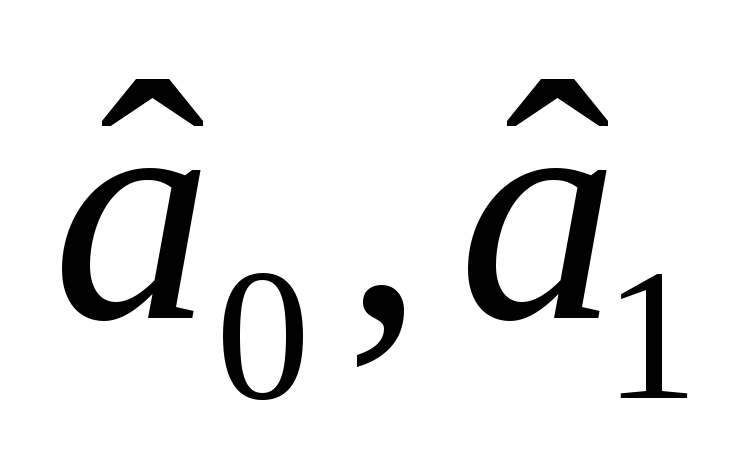4. — статистично незначущі.

У першому випадку залишки гетероскедастичні, причому існує чиста і мішана гетероскедастичність. У другому випадку залишки мають мішану гетероскедастичність. Третій випадок свідчить про наявність чистої гетероскедастичності. У четвертому випадку гетероскедастичність відсутня.

41. Перевірка наявності гетероскедастичності залишків на основі теста коефіцієнта рангової кореляції Спірмена.

Наявність чистої гетероскедастичності в сукупності спостережень можна виявити, розрахувавши рангові коефіцієнти кореляції Спірмена. На базі коефіцієнта Спірмена побудовано відповідний тест, алгоритм якого полягає в реалізації таких кроків:

Крок 1. Побудова простих економетричних моделей 1МНК залежної змінної (Y) з кожною з пояснювальних змінних (Х_j).

Крок 2. Визначення вектора залишків для кожної з побудованих моделей (u_j).

Крок 3. Ранжування вектора кожної пояснювальної змінної (Х_j) і кожного з векторів від меншого до більшого та заміна компонентів цих векторів їхніми рангами.

Крок 4. Визначення коефіцієнта рангової кореляції Спірмена за формулою:

,

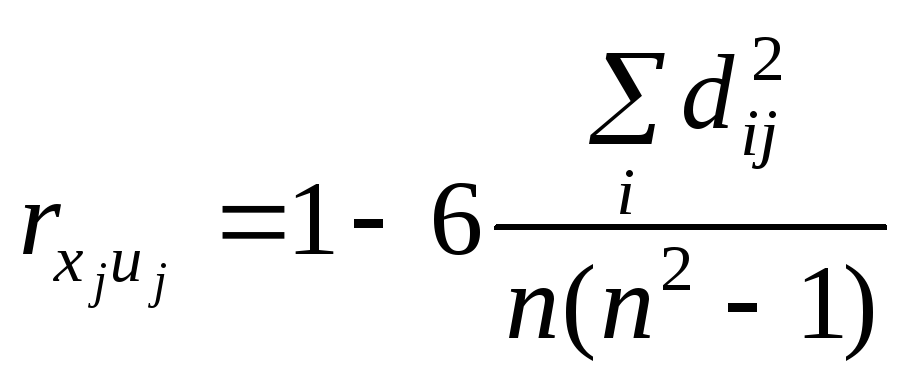де d_ij — різниця між рангами x_ij та ;

n — кількість спостережень; m – 1 — кількість пояснювальних змінних.

Крок 5. Розраховується t-статистика для визначення рівня статистичної значущості кореляції Спірмена за формулою:

.

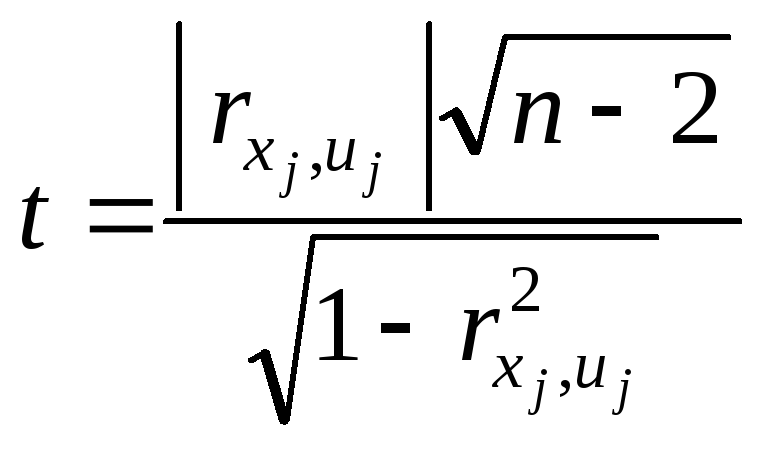Доведено, що ця характеристика має закон розподілу Стью- дента з кількістю ступенів свободи .

Якщо розраховане значення t-статистики перевищує критичне значення при ступені свободи n – 2 та вибраному рівні значущості , то гіпотезу про наявність гетероскедастичності потрібно прийняти. У протилежному випадку вона відхиляється.