Наращенные суммы и современные стоимости других видов постоянных рент

Кратко рассмотрим методики расчета наращенных сумм и современных стоимостей для некоторых разновидностей дискретных постоянных рент.

Ренты пренумерандо и ренты с выплатами в середине периодов. Напомним, что под рентой пренумерандо понимается рента с платежами в начале периодов. Легко понять, что каждый член такой ренты «работает» на один период больше, чем в ренте постнумерандо, обозначим ее здесь как S, больше в (1 + i) раз аналогичной ренты постнумерандо (рис. 5)

(88)

Коэффициент наращения годовой ренты пренумерандо

(89)

= R(1 + i)ⁿ рента пренумерандо

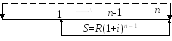
R

рента постнумерандо

(рис. 14)

Аналогичным путем получим для годовой ренты с начислением процентов m раз в году.

_{Для р срочных рент, у которых m = 1 и m ≠ р, получим}

;

Точно такая же зависимость наблюдается и между современными стоимостями и коэффициентами приведения рент постнумерандо и пренумерандо.

; и т.д.

Пример 18. Имеется постоянная рента пренумерандо равным 1000 руб., срок 4 года, процентная ставка – 10%. Рассчитать наращенную и современную стоимость.

Дано: R = 1000 руб. n = 4 года i = 10%	Решение: Так как согласно ( ) наращенная сумма равна =, то S4,10 для ренты постнумерандо равен = 1000 · 4,641 · 1,1 = 5105,1 (руб) Аналогично, современная стоимость: Ã = R · аn,i(1 + i) = 1000 · 3,1698 ·1,1 = 3486,78 (руб)
А - ? S - ?

Графическая иллюстрация

R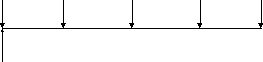= 1000 R = 1000 R = 1000 R = 1000 S=?

0 1 2 3 4

А = ?

Важной для практики является рента с платежами в середине периодов. Например, в случаях, когда поступления от производственных инвестиций распределяются более или менее равномерно, применение рент пренумерандо или постнумерандо для описания таких потоков может привести к некоторым смещениям в значении получаемых показателей. В таких ситуациях для уменьшения погрешности рекомендуется суммы поступлений за период относить к середине периодов. Наращенные суммы и современные стоимости таких рент находим умножением соответствующих обобщающих характеристик рент постунемарандо на множитель наращения за половину периода. Так, для современных стоимостей находим следующие отношения:

А_1/2 = А (1 + i)^1/2 при р = 1, m = 1

А_1/2 = А (1 + i)^1/2р при р > 1, m = 1

А_1/2 = А (1 + j/m)^m/2 при р = 1, m > 1

А_1/2 = А (1 + j/m)^m/2р при р > 1, m > 1

Пример . Определим поправочный множитель, необходимый для расчета современной стоимости ренты с платежами в середине периодов. Условия ренты постнумерандо: р = 12, m = 1, i = 10%.

Дано: р = 12 m = 1 i = 10%	Решение: Согласно ( ) поправочный множитель = (1 + i)1/2р или поправочный множитель = 1,1 1/24 = 1,00398.
ПМ - ?

Отложенные ренты

Начало отложенной (отсроченной) ренты приходится на какой-то момент в будущем относительно момента, по состоянию на который производится оценка современной величины ренты. Например, последовательное погашение кредита может производиться не сразу, а спустя некоторое время (льготный период) после поставки товара. Очевидно, что сдвиг во времени никак не отражается на величине наращенной суммы. Что касается современной стоимости, то ее можно определить следующим образом. Пусть рента выплачивается спустя t лет после некоторого начального момента времени. Эту ренту можно рассматривать как постоянную немедленную ренту с членом R , сроком n (причем под сроком этой ренты понимается период от начала выплат t до конца); ее современная стоимость (т.е. стоимость на момент t) равна A. Современная стоимость на начало периода отсрочки, равного t лет равна дисконтированной величине современной стоимости немедленной ренты (рис. 12). Для годовой ренты

_t A = A·v^t = A·a_n,i·v^t, (78)

где _tA – современная стоимость отложенной ренты

_tA = A·v^t A = R·a_n,i

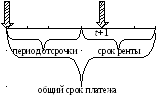
1 2 … t .…n₀-1 n₀

t n

Рис. 12. Современная стоимость отсроченной ренты

Пример . Годовая рента постнумерандо характеризуется параметрами: R = 4 млн. руб., n = 5 лет. Рента начинает выплачиваться спустя 1,5 года после ее начала, т.е. общий срок ренты составляет 6,5 лет. Определить современную стоимость. Процентная ставка – 18,5%.

Дано: R = 4 млн. руб. n = 5 лет t = 1,5 года i = 18,5%	Решение: Найдем сначала современную стоимость годовой ренты постнумерандо: (млн.руб) Дисконтируя эту сумму на 1,5 года получим искомый результат: 1,5А = 12,368 · 1,185-1,5 = 9,588 (млн. руб.)
1,5А - ?

Современная стоимость отложенной ренты используется при решении целого ряда задач, чаще всего в расчетах, связанных с выплатами рзличного рода накоплений. Для иллюстрации обсудим одну из подобных задач. Пусть годовая ограниченная рента постнумерандо делится во времени между двумя участниками (например, речь идет о передаче собственности). Рента имеет параметры: R, n. Условия деления: а) каждый участник получает 50% капитализированной стоимости ренты; б) рента выплачивается последовательно – сначала первому участнику, затем второму.

Решение задачи сводится к расчету срока получения ренты первым участником, обозначим его как n₁. В оставшийся срок деньги получает второй участник. Таким образом, первый участник получает немедленную ренту, второй – отложенную. Из принятых условий деления ренты следует:

А₁ = _n1А₂; Rа_n1;i = Rа_n2;ivⁿ¹.

Учитывая, что n₂ = n – n₁, находим:

После ряда преобразований получим

( )

Результат зависит только от общего срока ренты и процентной ставки, которая учитывается в расчете.

Пример . Срок годовой ренты постнумерандо 10 лет, i = 20%. Пусть рента делится между двумя участниками на тех условиях, которые были выше приняты при выводе формулы. Определить сроки получения ренты каждым участником.

Дано: n = 10 лет i = 20%	Решение: Доля второго участника – следующие 7 лет.
n1 - ?; n2 - ?

Вечная рента. Напомним, что под вечной рентой понимается ряд платежей, количество которых не ограничено – теоретически она выплачивается в течении бесконечного числа лет. В практике иногда сталкиваются со случаями, когда есть смысл прибегнуть к такой абстракции, например, когда предполагается, что срок потока платежей очень большой и конкретно не огаваривается. Примером могут служить некоторые виды облигаций.

Очевидно, что наращенная сумма вечной ренты равна бесконечно большой величине. На первый взгляд представляется бессодержательным и определение современной стоимости такой ренты. Однако это далеко не так. Современная величина, которая определяется весьма просто.

(99)

Таким образом, современная стоимость вечной ренты зависит только от размера члена ренты и процентной ставки.

(100)

Т.е. член вечной ренты равен проценту от ее капитализированной стоимости.

Нетрудно убедиться в том, что отдаленные платежи оказывают весьма малое влияние на величину коэффициента приведения. С ростом n прирост этого показателя уменьшается. В силу сказанного при больших сроках ренты и высоком уровне ставки для определения современной стоимости можно воспользоваться формулой (99) без заметной потери точности. Например, для ограниченной ренты при i = 20%, n = 100 и R = 1 получим точное значение: А = 4,999999, а по формуле (99) находим А_∞ = 5.

Для других видов рент получим:

при р>1, m=1;

при р = m > 1.

Пример . Требуется выкупить вечную ренту, член которой равен 5 млн. руб., выплачиваемых в конце каждого полугодия. Капитализированная стоимость такой ренты при условии, что для ее определения применена годовая ставка 25%, составит:

Рента с периодом платежей, превышающим год. В анализе производственных инвестиционных проектов иногда встречаются с рентами, члены которых выплачиваются с интервалами, превышающими год. Определим наращенную сумму и современную стоимость таких рент.

Пусть r – временной интервал между двумя членами ренты, проценты начисляются раз в году. В этом случае современная стоимость первого платежа составит на начало ренты величину Tv^r, второго – Tv^2r, последнего члена – Tvⁿ, где Т – величина члена ренты, n – срок ренты, кратный r. Последовательность дисконтированных платежей представляет собой геометрическую прогрессию с первым членом Tv^r, знаменателем v^r и ; числом членов п/r. Сумма членов такой прогрессии при условиb, что Т= 1, равна:

(101)

Разумеется, указанное в формуле соотношение коэффициентов приведения и наращения можно использовать в случаях, когда r — целое число лет.

ПРИМЕР . Сравниваются два варианта строительства неко­торого объекта. Первый требует разовых вложений в сумме 6 млн руб. и капитального ремонта стоимостью 0,8 млн руб. каж­дые 5 лет. Для второго затраты на создание равны 7 млн руб., на капитальный ремонт — 0,4 млн руб. каждые 10 лет. Временной го­ризонт, учитываемый в расчете, — 50 лет.

Сумма затрат при условии, чтоi = 10 %, оценивается для каждого варианта в следующих размерах:

Таким образом, в финансовом отношении варианты оказываются равноценными при принятом уровне процентной ставки. Чем ставка выше, тем меньше влияют на результат затраты на ремонт. Так, если сравнение производится при ставке 20%, то получим А₁, = 6,39, А₂ = 7,05.

Переменная процентная ставка. На практике иногда сталки­ваются с потоками платежей, предполагающих применение пе­ременных во времени процентных ставок, например, при рест­руктурировании задолженности. Так, в последнем случае для облегчения положения должника применяются низкие ставки в первые годы выплат процентных платежей и более высокие в последующие.

Изменения размеров ставок могут быть какими угодно. Ес­ли же эти изменения "ступенчатые", то при определении нара­щенной суммы и современной стоимости постоянной ренты резонно применить стандартные формулы. Пусть для постоянной ренты постнумерандо со сроком 10 лег предусматриваются два уровня процентной ставки, применяемые по пятилетиям. В этом случае