Консолидирование задолженности

Одним из распространенных случаев изменения условий платежей являетсяконсолидация (объединение) платежей. Пусть платежи S₁, S₂,..., S_m со сроками n₁, n₂, ... , n_m заменяются одним в сумме S₀ и сроком n₀. В этом и подобных случаях составляется уравнение эквивалентности, причем возможны два случая: если задается срок платежа – n₀, то находится сумма S₀, и, наоборот, если задана сумма консолидированного платежа – S₀, то определяется срок n₀.

При определении суммы консолидированного платежа в общем виде, когда n₁<n₂<…<n_m, причем n₁<n₀<n_m, искомую величину суммы консолидированного платежа находим из уравнения эквивалентности как сумму наращенных дисконтированных платежей.

При применении простых процентных ставок, получим

, (55)

где S_j – размеры объединяемых платежей со сроками n₁<n₀,

S_k – размеры платежей со сроками n_k > n₀,

t_j = n₀ – n_j; t_k = n_k – n₀.

Графическая иллюстрация этого случая приведена на рис. 10.

+

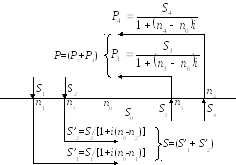
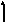
S₀ = S + P

Рис. 10. Нахождение суммы консолидированного платежа

Пример 37.

Два платежа S₁ = 250000 руб. и S₂ = 150000 руб. со сроками соответственно 100 дней и 200 дней (отсчитываемых от одной даты) заменяются одним платежом со сроком 220 дней. Заинтересованные стороны согласились на 6% годовых по простой ставке. k = 360 дней.

Дано: S1 = 250000 руб. S2 = 150000 руб. n1 = 100 дней n2 = 200 дней n3 = 220 дней i = 6%	Решение: Для того, чтобы найти сумму заменяющего платежа, составляем уравнение эквивалентности: S3 = S1 ∙ [1 + (n3 – n1) ∙ i] + S2 ∙ [1 + (n3 – n2) ∙ i] (смотри графическую иллюстрацию) S1 = 250000 руб. S2 = 150000 руб. S3 - ?
S3 - ?

100 200 i = 6% 220

i = 6% наращение

наращение

То есть платежи 250000 руб. и 150000 руб. наращиваются соответственно на 120 дней (220 – 100) и 20 дней (220 – 200):

Пример 38.

Используя простые проценты, объединим три платежа со сроками 15.05, 15.06 и 15.08. Суммы платежей соответственно составляют 10000 руб., 20000 руб. и 15000 руб. Согласованная процентная ставка равна 8%. Срок нового платежа 01.08. Требуется определить сумму нового платежа, k = 365 дней. Проценты точные.

Дано: S1 = 10000 руб. S2 = 20000 руб. S3 = 15000 руб. i = 8%	Решение: Находим номера дат уплаты (приложение 1) n1 : 15.05 – 135-й день в году; n2 : 15.06 – 166-й день в году; n3 : 15.08 – 227-й день в году; n4 : 1.08 – 213-й день в году. То есть: n4 – n1 = 213 – 135 = 78 (дней) n4 – n2 = 231 – 166 = 47 (дней) n3 – n4 = 227 – 213 = 14 (дней)
S4 - ?

Графическая иллюстрация

S₁ = 10000 руб. S₂ = 20000 руб. S₄ - ? S₃ = 15000 руб.

дисконтирование

i = 8% n = 14

15.05 15.06 i = 8% n = 47 01.08 15.08

i = 8% n = 78 наращение

Уравнение эквивалентности:

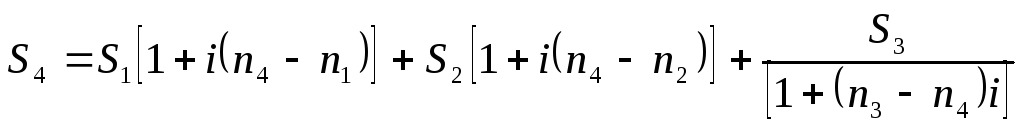
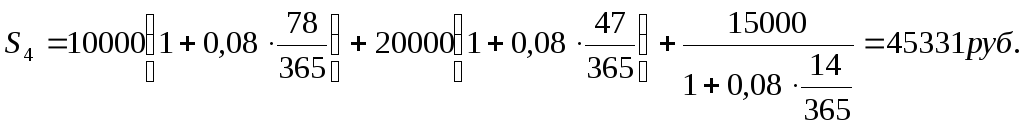При применении сложных процентных ставок уравнение эквивалентности выглядит следующим образом (n₁<n₀<n_m)

. (56)

При определении срока консолидированного платежа уравнение эквивалентности удобно представить в виде равенства современных стоимостей соответствующих платежей. Получим соответственно:

, откуда

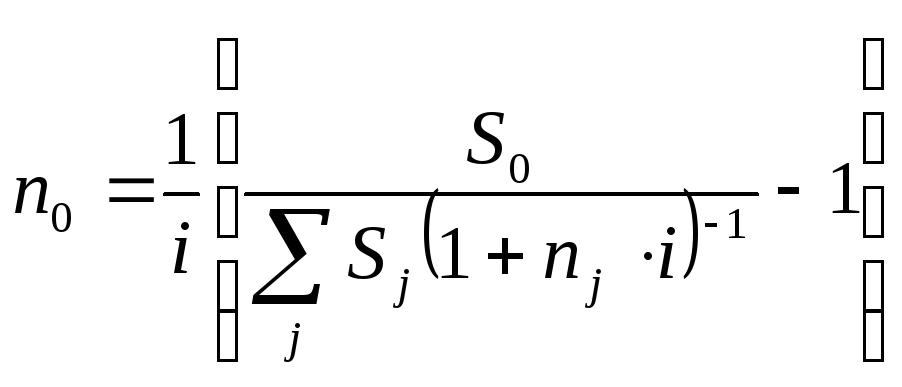. (57)

, откуда

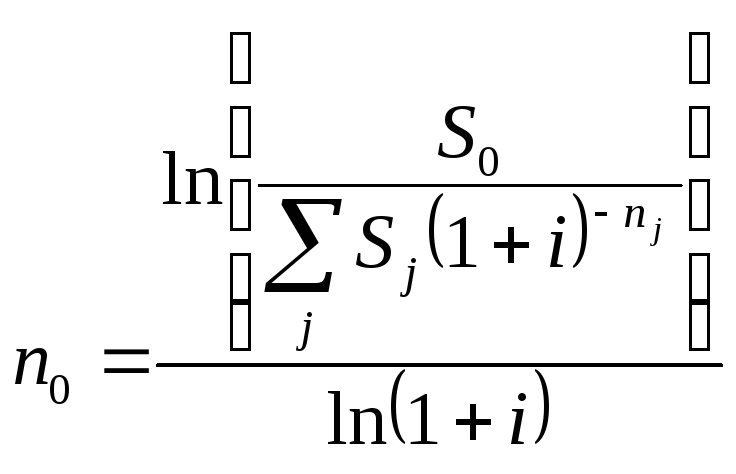^. (58)

Принцип эквивалентности можно применить не только для определения сроков и суммы консолидированного платежа, но и при определении вида процентных ставок.

Замена одного вида ставки на другой при соблюдении принципа эквивалентности не изменяет финансовые взаимоотношения сторон в рамках одной операции. Для них безразлично, какой вид ставки фигурирует в контракте. Такие ставки тоже называются эквивалентными.

Формулы эквивалентности ставок можно получить, приравняв попарно множители наращения.

Следует отметить, что для всех вариантов изменения условий контрактов нет годовых формул. В каждом случае необходимо исходить из принципа эквивалентности финансовых последствий, который отражает следующее положение: сумма приведенных платежей по условиям прежних контрактов равна сумме приведенных на тот же момент времени платежей по новым условиям измененных контрактов. Вид этих уравнений определяется на основании логики.

Пример 39.

Имеются долговые обязательства уплаты 10000 руб. 01.11 и 5000 руб. 01.01 нового года. Эти обязательства предлагается заменить новыми: должник уплачивает 01.12 сумму 6000 руб., остальной долг он должен погасить 01.03 нового года. Сумма нового платежа определяется из условия, что простая процентная ставка будет равна 6% годовых. Требуется определить сумму нового платежа 01.03, k = 365 дней. Проценты точные.

Дано: S1 = 10000 руб. S2 = 5000 руб. S3 = 6000 руб. i = 6%	Решение: В качестве даты приведения (базовой даты) применим срок погашения неизвестного платежа, т.е. 01.03 нового года, тогда
S4 - ?

S₁ = 10000 руб. S₂ = 5000 руб. наращение

наращение

01.11 01.12 01.01 01.03

n₁ n₂ n₃ n₄

наращение

S₃ = 6000 руб. S₄ - ?

Уравнение эквивалентности:

01.11 – 01.03 – 120 дней;

01.01 – 01.03 – 59 дней;

01.03 – 01.12 – 90 дней, тогда

откуда S₄ = 9158 рублей.

Пример 40.

Два векселя: один номинальной стоимости 20000 руб. и сроком погашения 10.06 и другой номинальной стоимости 50000 руб. со сроком погашения 01.08 заменяются одним с продлением срока до 01.10. При объединении векселей применена простая учетная ставка, равная 8% годовых. Требуется определить сумму нового платежа.

Дано: S1 = 20000 руб. S2 = 50000 руб. d = 8%	Решение: Для решения этой задачи используем выражение для операций с простой учетной ставкой. Уравнение эквивалентности:
S3 - ?

S₁ = 20000 S₂ = 50000

наращение

наращение

10.06 1.08 1.10

S₃ - ?

Легко определить, что сроки пролонгации платежей в описанной ситуации составят соответственно 113 дней и 61 день (n₁ и n₂), тогда

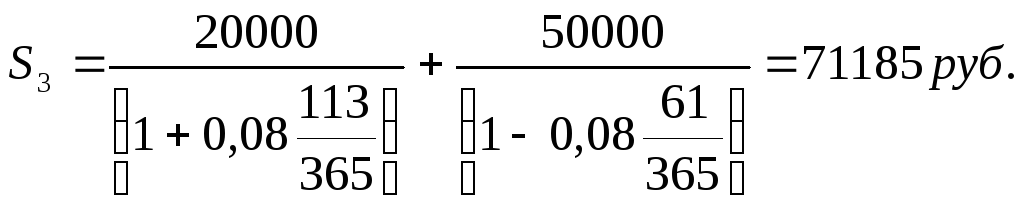
При изменении условий платежей необходимо очень внимательно подходить к выбору даты приведения платежей (это касается использования простой ставки процентов).

Выбор формы расчетов

Теперь выясним, какая из форм расчетов (процентов) наиболее выгодна для вкладчика (кредитора) и заемщика.

Для этого произведем вычисления будущей стоимости денег различными рассмотренными выше способами, сравним их и сделаем выводы.

Пусть ссуда или доходная сумма денег равна 100 руб., процентная ставка – 0,03, а учетная ставка – 0,03, период погашения – 5 лет.

Р = 100 руб.

i = 0,03 (3% годовых)

d = 0,03 (3% годовых)

n = 5 лет

1. Определим будущую стоимость исходной суммы по ставке i:

а) по простым процентам:

б) по сложным процентам:

2. Найдем доход, выплачиваемый в момент предоставления кредита по учетной ставке:

а) по простым процентам:

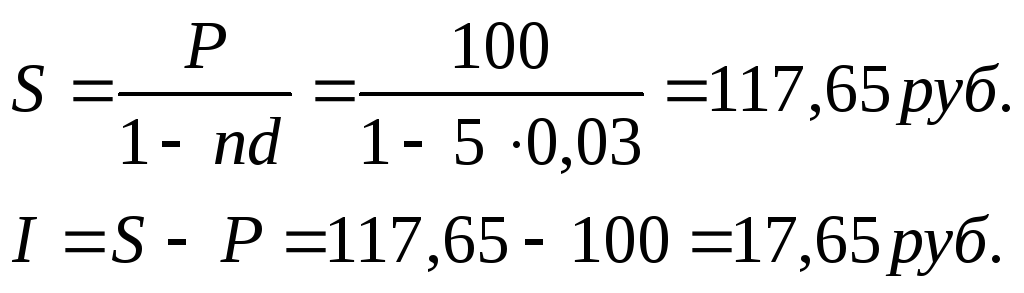
б) по сложным процентам:

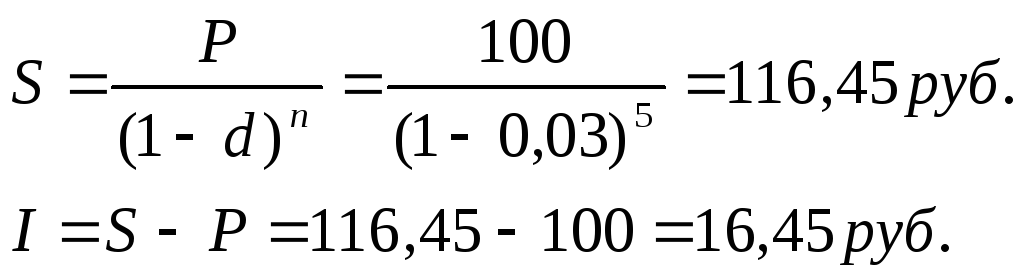
Из соотношения ставок простых и учетных процентов вытекает, что если эти ставки равны, т.е. d = i, то величина годового дохода не меняется. Например, годовой доход в 15 руб. можно получить с исходной суммы 100 руб., данной на 5 лет при ставке i = 0,03, и доход в 15 руб. можно получить, предоставив кредит 85 руб. при учетной ставке d = 0,03. Но так как доход по авансовым процентам (по учетной ставке) получается в момент предоставления кредита, дачи суммы в долг, то, следовательно, расчет по авансовым процентам для кредитора выгоднее, чем для дебитора. Эта выгодность возрастает, если расчет осуществляется не за один год, а за несколько лет.

В нашем примере доход в 16,45 руб. кредитор получает с суммы дачи в долг 100 руб. в момент предоставления долга при авансовых сложных процентах при n = 5 лет и d = 0,03 и доход в 15,93 руб. – при n = 5 лет и при i = 0,03 при сложных процентах.

Выгодность тех или иных форм процентов связана и с периодом наращения денег. Если сравнивать наращение средств по простым процентам «со 100» [S = Р(1 + ni)] и сложным процентам «со 100» [S = Р(1 + i)ⁿ], то при периоде наращения денег более 1 года (n > 1) сложные проценты более «сильные», чем простые. Так, при i = 0,03 и n = 5 по простым процентам доход за 5 лет со 100 руб. равен:

по сложным процентам:

Однако при периоде наращения менее одного года простые проценты «сильнее», чем сложные.

Докажем это.

Пусть i = 0,03, Р = 100 руб., t/k = ½ года. Определим S:

а) по простым декурсивным процентам:

б) по сложным декурсивным процентам:

Следовательно, при периоде наращения менее одного года для кредитора предпочтительнее простые проценты.

Сопоставляя сложные и сложные авансовые проценты, можно сделать вывод, что наращение денег по правилу «на 100» по сложным авансовым процентам «сильнее», чем наращение по сложным по правилу «со 100», поскольку при равенстве i = d величина

больше величины

«на 100» «со 100»

Если сравнивать авансовые проценты, можно убедиться, что сложные авансовые проценты по правилу «на 100» при периоде больше одного года (n > 1) «слабее», чем простые авансовые по правилу «на сто».

В нашем примере при d = 0,03, n = 5 и Р = 100 руб.

(«на 100» простые) («на 100» сложные)

Однако при периоде наращения менее одного года сложные авансовые «сильнее», чем простые авансовые проценты.

Например, Р = 100 руб., d =0,03, t/k = ½ года.

Тогда

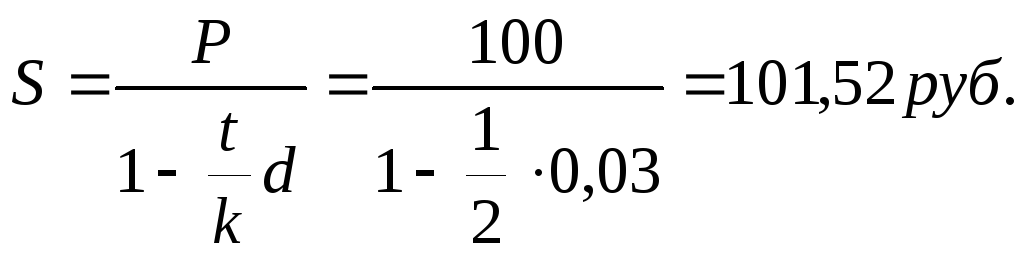
(«на 100» простые) («на 100» сложные)

Эти особенности и соотношения учитываются при осуществлении ссудных, вкладных и других операций.

Погашение задолженности частями

Контур финансовой операции

Контур финансовой операции – это графическое изображение процесса погашения краткосрочной задолженности частичными (промежуточными) платежами. Финансовая или кредитная операции предполагают сбалансированность вложений и отдачи. Понятие сбалансированности можно пояснить на графике, представленном на рис. 11

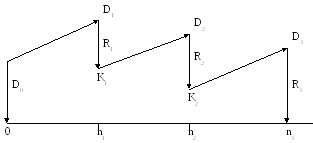
Рис. 11 Контур финансовой операции

Пусть ссуда в размере D₀ выдана на срок t. На протяжении этого срока в счет погашения задолженности производятся два промежуточных платежа R₁ и R₂, а в конце срока выплачивается остаток задолженности R₃, подводящий баланс операции.

На интервале времени t₁ задолженность возрастает до величины D₁. В момент t₁ долг уменьшается до величины К₁ = D₁ – R₁ и т. д. Заканчи­вается операция получением кредитором остатка задолженности R₃. В этот момент задолженность полностью погашается.

График такого типа называют контуром финансовой операции. Сбалансированная операция обязательно имеет замкнутый контур, т. е. последняя выплата полностью покрывает остаток задолженности. Контур операции обычно применяется при погашении задолженности частичными промежуточными платежами.

С помощью последовательных частичных платежей иногда погаша­ются краткосрочные обязательства. В этом случае существуют два ме­тода расчета процентов и определения остатка задолженности. Это актуарный метод, он применяется в операциях со сроком более года. Другой метод назван правилом торговца, или коммерческим прави­лом. Он обычно применяется коммерческими фирмами в сделках со сроком не более года.

Следует отметить, что при начислении процентов, как правило, используются обыкновенные проценты с приближенным числом дней временных периодов.

Актуарный метод

Актуарный метод предполагает последовательное начисление про­центов на фактические суммы долга. Частичный платеж идет в пер­вую очередь на погашение процентов, начисленных на дату платежа. Если величина платежа превышает сумму начисленных процентов, то разница идет на погашение основной суммы долга. Непогашенный ос­таток долга служит базой для начисления процентов за следующий период и т. д. Если же частичный платеж меньше начисленных про­центов, то никакие зачеты в сумме долга не делаются. Такое поступле­ние приплюсовывается к следующему платежу.

Для случая, показанного на рис. 11, получим следующие расчетные формулы для определения остатка задолженности:

K

(59)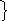

₁ = D₀ (1 + t₁i) – R₁; K₂ = K₁ (1 + t₂i) – R₂;

K₂ (1 + t₃i) – R₃ = 0,

где t₁, t₂, t₃ – периоды времени, заданные в годах; i – годовая процентная ставка.

Правило торговца

Правило торговца является другим подходом к расчету частичных платежей. Здесь возможны две ситуации:

1. Если срок ссуды не превышает года, сумма долга с начисленными за весь срок процентами остается неизменной до полного погашения.

Одновременно идет накопление частичных платежей с начислен­ными них до конца срока процентами.

2. В случае, когда срок превышает год, указанные ранее расчеты делаются для годового периода задолженности. В конце года из суммы задолженности вычитается наращенная сумма накопленных час­тичных платежей. Остаток погашается в следующем году.

При общем сроке ссуды t ≤ 1 можно записать следующее выражение:

(60)

где S — остаток долга на конец срока; D — наращенная сумма долга; К — наращенная сумма платежей; R_j — сумма частичного платежа; tj — интервал времени от момента платежа до конца срока; m — число частичных (промежуточных) платежей; Р — ссуда банка.

Пример 41.

Ссуда в размере 3000000 руб. выдана банком 20 января на срок 1 год. На протяжении этого срока в счет погашения задолженности производятся платежи в банк: 20 апреля в размере 500000 руб., 20 июля в сумме 200000 руб., 20 октября в размере 800000 руб. На ссуду банк предусматривает начисление простых процентов по ставке 30 % годовых. Рассчитать контур финансовой операции для актуарного метода и ме­тода торговца и определить размер погасительного платежа в обоих случаях. Результаты расчета сравнить.

Решение.

Вычислим размер погасительного платежа актуарным методом.

20 января долг банку составил 3000000 руб.

20 апреля долг с процентами составил:

3000000 ∙ (1 + 0,3 ∙ 1/4) = 3000000 руб. + 225000 руб. = 3225000 руб.

В банк поступило 500000 руб., что больше начисленных процентов 225000 руб., поэтому вычитаем из долга 500000 руб. Таким об­разом, 20 апреля остаток долга составил:

3225000 руб. - 500 000 ден. ед. = 2725000 руб.

20 июля долг с процентами составит:

2725000 ∙ (1 + 0,3 ∙ 1/4) = 2725000 руб. + 204375 руб. = 2929375 руб.

В банк поступило 200000 руб. < 204375 руб., поэтому этот пла­теж присоединяем к платежу 20 октября, на эту дату долг с процента­ми составит:

2725000 ∙ (1 + 0,3 ∙ 1/2) = 2725000 руб. + 408750 руб. = 3133750 руб.

В банк поступило 800000 руб., что больше начисленных процентов 408750 руб. поэтому вычитаем из долга 800000 руб. Таким об­разом, 20 октября остаток долга составит:

3133750 руб. - 200000 руб. - 800000 руб. = 2133750 руб.

20 января долг с процентами составит:

2133750 руб. (1 + 0,3 ∙ 1/4) = 2293781,25 руб.,

которая является размером последнего погасительного платежа.

Теперь вычислим размер погасительного платежа методом торговца.

На конец срока (1 год) остаток долга составит:

3000000 ∙ (1 + 0,3) – 500 000 ∙ (1 + 0,3 -3/4) – 200000 ∙ (1 + 0,3 ∙ 1/2) – 800000 ∙ ∙(1 + 0,3 ∙ 1/4) = 3900000 руб. – 612500 руб. – 230000 руб. – 860000 руб. =

= 2197500 руб.

Таким образом, размер погасительного платежа, вычисленный акту­арным методом, составит 2293781,25 руб., методом торгов­ца — 2197500 руб. Для банка выгоден расчет по актуарному мето­ду, для клиента — по методу торговца.

Нетрудно понять, что актуарный метод в известной мере нарушает принцип погашения простых процентов, так как проценты начисляются не на первоначальную сумму долга, а на остаток задолженности, который в ряде случаев может частично содержать ранее погашенные проценты. Такая ситуация, разумеется не возникнет тогда, когда на каждом этапе выплачиваются только проценты.

Переменная сумма счета и расчет процентов.

Рассмотрим ситуацию, когда в банке открыт счет, который изменяется в течении срока хранения: денежные средства снимаются, делаются дополнительные взносы.

В банковской практике в этой ситуации используется правило – общая начисленная на весь срок сумма процентов равна сумме процентов, начисленных на каждую из постоянных на некотором отрезке времени сумм.

Это касается и дебетовой, и кредитовой части счета. Разница лишь в том, что кредитовые проценты вычитаются.

Для начисления процентов на такие постоянные суммы используютпроцентные числа.

,

или

(61)

где t_j – длительность j-го периода в днях, Р_j – сумма на вкладе j-го периода.

Для определения суммы процентов, начисленной за весь срок, все процентные числа складываются и их сумма делится на постоянный делитель D – называемый «дивизор».

или

(62)

где K – временная база (число дней в году, т.е. 360, 365, 366);

i – годовая ставка простых процентов, %.

Таким образом, вся абсолютная сумма начисленных процентов рассчитывается следующим образом:

или

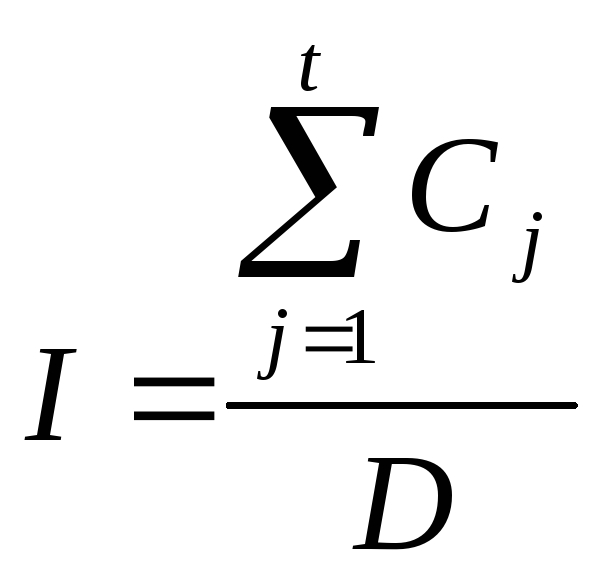(63)

При закрытии счета владелец получит сумму, равному последнему значению суммы на счете плюс сумма процентов.

Пример 42.

Вкладчиком 20 января в банке был открыт счет до востребования в размере Р₁ = 1000 руб., процентная ставка по вкладу составляла i = 15% годовых. Дополнительный взнос на счет составил R₁ = 2000 руб. и был сделан 10 марта. Снятие со счета в размере R₂ = 1500 руб. зафиксировано 3 мая. 10 октября того же года счет был закрыт. Определить сумму процентов и общую сумму, полученную вкладчиком при закрытии счета. При расчетах принять схему 360/360, простые проценты с приближенным числом дней ссуды.

Графическая иллюстрация задачи

Р₁ = 1000 R₁ = 2000 S - ?

I - ?

20.01 10.03 3.05 10.10

R₂ = 1500

Решение:

В задаче имеются три периода, в течении которых сумма на счете оставалась неизменной: с 20 января по 10 марта (Р₁ = 1000 руб.; t₁ = 10 + 30 + + 10 = 50), с 10 марта по 3 мая (t₂ = 20 + 30 + 3 = 53; Р₂ = Р₁ + R₁ = 1000 руб. + + 2000 руб. = 3000 руб.), с 3 мая по 10 октября (Р₃ = Р₂ – R₂ = 3000 руб. –

– 1500руб. = 1500 руб.; t₃ = 26 + 4 ∙ 30 + 10 = 156).

Найдем процентные числа:

С₁ = Р₁t₁/100 = 1000 ∙ 50/100 = 500;

С₂ = Р₂t₂/100 = 3000 ∙ 53/100 = 1590;

С₃ = Р₃t₃/100 = 1500 ∙ 156/100 = 2340.

Постоянный делитель

D = K/i = 360/15 = 24.

Сумма процентов

Сумма, выплачиваемая при закрытии счета

Р₃ + I = 1500 руб. + 184,58 руб. = 1684,58 руб.

Из алгоритма расчета следует, что на каждую сумму, добавляемую на счет или снимаемую со счета, начисляются проценты с момента совершения соответствующей операции до закрытия счета. Эта схема соответствует правилу торговца.

Пример 43.

На расчетный счет предприятия поступили средства: 15.01 – 890000 руб., 20.03 – 17278577 руб.; дебетовое сальдо с прошлого квартала на 01.01 текущего года – 27160 руб. Снятие средств осуществилось 22.02 – 500000 руб. Процентная ставка – 10% годовых на остаток на счету. Подведем итоги на 31.03 текущего года по текущему счету предприятия в банке.

Решение:

1. Исходные данные заносим в табл. 7 в гр. «Сумма»: поступление – в дебет, расход – в кредит.

2. В гр. «Дни» записываем t, т.е. порядковый номер дня, на который подводим итоги, минус порядковый номер дня операции.

3. Далее в гр. «Процентное число» записываем, округляя до целых рублей:

500000 ∙ 37 : 100 = 185000 (1)

27160 ∙ 89 : 100 = 24172 (2) и т.д. (3), (4)

4. Затем на балансовой строке процентных чисел подводим их итог: складываем процентные числа дебета и отдельно кредита. Большая сумма пишется в баланс в дебет и кредит (5), а сальдо (разница между суммой процентных чисел дебета и кредита) проставляется там, где сумма меньше (6).

5. Исчисляем процентный платеж исходя из сальдо процентных чисел и дивизора (Y : i (в процентах)):

(7)Таблица 7

Расчеты при ведении текущего счета

Кредит

Дата снятия	Дни (t)	Сумма (PV)	Процентное число (PV ∙ t/100)
22.02 Сальдо процентных чисел	90 (N31.03) – 53 (N22.02) = 37	500000	185000 (1) 2407315 (6)
31.03			2592315 (5)

Дебет

Дата снятия	Дни (t)	Сумма (PV)	Процентное число (PV ∙ t/100)
01.01 15.01 20.03 31.03 (процентный платеж)	90 (N31.03) – 1 (N01.01) = 89 90 (N31.03) – 15 (N15.01) = 75 90 (N31.03) – 79 (N20.01) = 11	27160 890000 17278577 66870 (7)	24172 (2) 667500 (3) 1900643 (4)
31.03			2592315 (5)

Таким образом, на 31.03 средства на счете с процентами составят:

+	27160
+	890000
+	17278577
+	66870
–	500000
17762607