Практичні завдання Побудова двомірних графіків

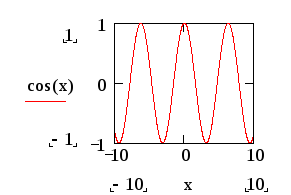
Приклад 1. Побудувати графік функції y(x)=cos(x)

Викличте шаблон для побудови графіків в декартових координатах: Math (Математика)  Graph (Інструменти графіків) X-Y Plot (Декартів графік) з'явиться шаблон для побудови графіків В шаблоні графіка під віссю х у середньому квадратику наберіть х В шаблоні графіка ліворуч вісі у в середньому квадратику наберіть cos(x) Натисніть мишкою поза шаблоном графіку і графік з’явиться на екрані

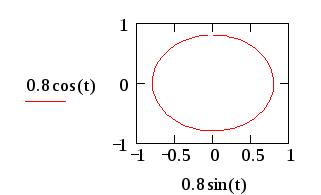
Приклад 2. Побудувати графік функції, яка задана параметрично x=0.8sin(t), y=0.8cos(t) t(0;2)

• Задайте діапазон дискретної змінної t:=0,0.1..2

• Викличте шаблон для побудови декартового графіка

• Заповніть шаблон за рисунком

• Натисніть мишкою поза шаблоном графіку

Приклад 3. Побудувати графік функції, в полярних координатах .

У полярних координатах кожна точка задається кутом f і довжиною радіуса-вектора r(f). Графік функції будується при зміні кута f у визначених межах, найчастіше від 0 до 2

• Задайте діапазон дискретної змінної f:=0,0.1..2

• Викличте шаблон для побудови графіка в полярних координатах

• Заповніть шаблон за рисунком

• Натисніть мишкою поза шаблоном графіку

f:=0,0.1..2

Анімація графіків

Приклад 4. Зобразити точку, яка рухається за функцією f(x)=sin(x)

В Mathcad вбудовано дискретну змінну FRAME, яка приймає цілі значення (за замовчуванням від 0 до 9). Функція, графік якої треба спостерігати в розвитку, повинна бути функцією цієї змінної і визначати кадри анімованого рисунку.

• Задайте функцію f(x):=sin(x)

• Нехай а – визначається за допомогою змінної FRAME

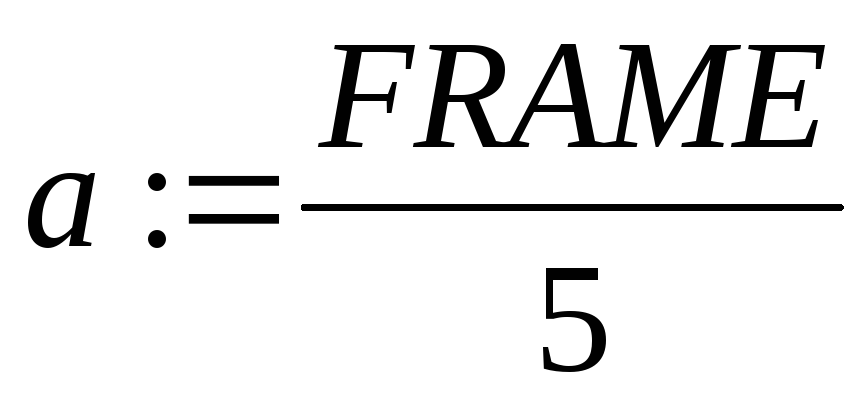
• Побудуйте графіки функцій f(x) i f(a), відформатуйте їх

• Виконайте команду View (Вид)  Animate (Анімація). Виділіть область графіку, задайте межі зміни кадрів від 0 до 50. Натисніть кнопку Анімація

• Для перегляду анімованого рисунка використовуйте спеціальний програвач Playback.

• Збережіть відеозображення на диску з розширенням .avi

Функція

значення а

значення f(a)

Графічне розв'язування рівнянь

Приклад 5. Розв’язати рівняння

• Введіть функцію

• Викличте шаблон для побудови декартового графіку і заповніть шаблон (під віссюx в середньому квадратику наберіть х; ліворуч від вісі y в середньому квадратику наберіть f(x).

• Натисніть мишкою поза шаблоном графіка і графік з’явиться на екрані.

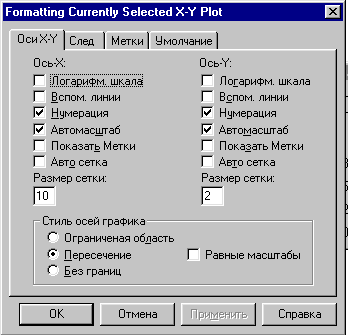
• Для форматування графіку двічі клацніть мишкою в області графіка, виберіть вкладку X-Y Axis (Вісі X-Y), і встановіть параметри за малюнком:

• Зконтекстного меню графіка (права кнопка миші) виберіть пунктTrace…(Трасування). У вікні графіка, з'явиться перехрестя з двох чорних пунктирних ліній. Якщо встановити прапорець Track data points (Слід точок даних), то при трасуванні покажчик автоматично встановлюється на точку найближчої кривої, відслідковуючи її хід;

• За допомогою миші перемістіться за графіком і в першому наближенні визначте координати точок перетину графіку з віссю 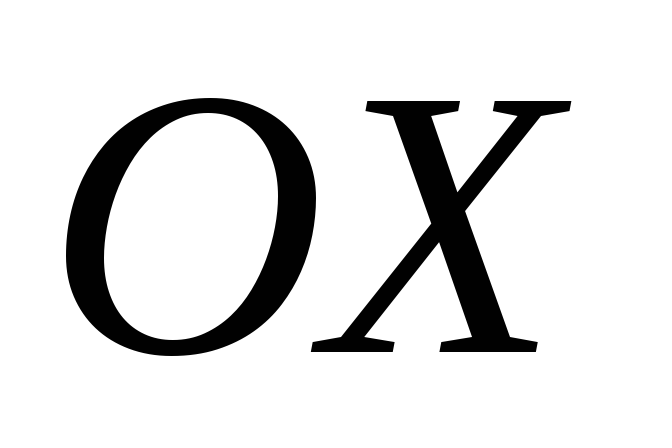– це і буде розв’язок рівняння.

Якщо велика точність обчислень не вимагається, то з такими висновками можна погодитись. Однак, якщо вимагається дещо вища точність результатів, то, можна збільшити масштаб графіку.

• Виберіть з контекстного меню команду Zoom (Масштаб), за допомогою якого можна збільшити будь-яку область графіка. Виділіть мишкою частину графіку і натисніть кнопку Zoom (Масштаб +). Ділянка графіка збільшиться до розмірів всього вікна.

З цього графіку буде видно, що корені рівняння:

Приклад 6. Розв’язати графічно систему рівнянь.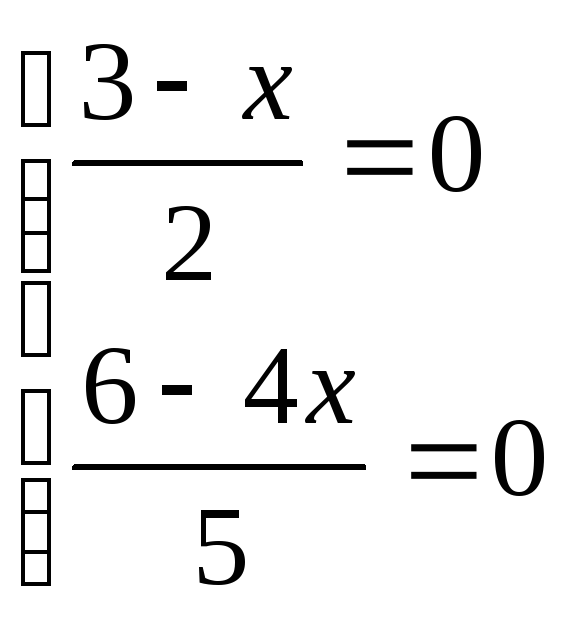

• Викличте шаблон для побудови декартового графіку

• Ушаблоні для побудови графіків введіть знизу зміннух, ліворуч введіть через кому функції, графіки яких ми будуємо 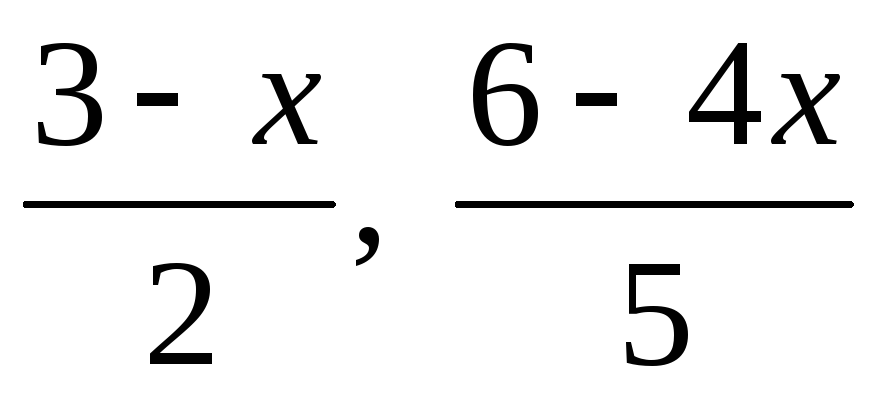, натисніть Enter і в шаблоні з'явиться графік 2-х функцій

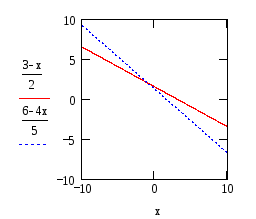
• За допомогою трасування знайдіть наближено корінь системи рівнянь – точку перетину графіків функцій

Розв’язок системи: x=-1.12

y=2.112

Приклад 7. Розв’язати нерівність

• Викличте шаблон для побудови декартового графіку і заповніть шаблон (під віссю у середньому квадратику наберітьх; ліворуч від вісі 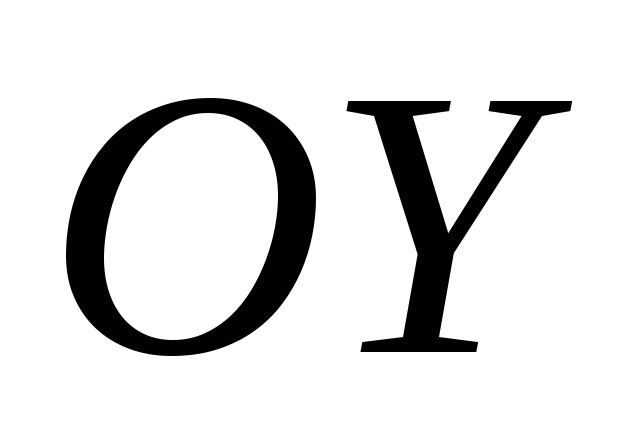в середньому квадратику наберіть,

• Натисніть мишкою поза шаблоном і графіки з’являться на екрані.

• Для форматування графіку двічі клацніть мишкою на графіку, виберіть вкладку Traces (Cлід), і встановіть параметри за малюнком:

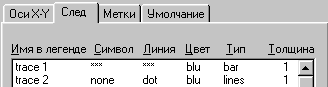
• Після встановлення всіх необхідних параметрів отримаємо графік:

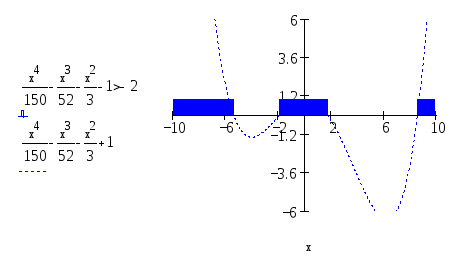
З графіку, за допомогою трасування, видно, що розв’язком нерівності є множина