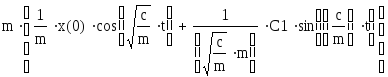Геометричний зміст задач лінійного програмування

Оскільки в задачі тільки дві змінні, можна розглянути геометричну інтерпретацію даної задачі на площині і знайти розв’язок геометричними методами.

1. Розв’яжемо систему нерівностей і отримаємо множину допустимих розв’язків задачі (див. додаток);

2. Тепер знайдемо точку, в якій лінійна функція набуває найменшого значення. Лінійну функцію можна представити як сім’ю паралельних прямих(-будь-яке число).

Побудуємо, наприклад, лінію (=0)

Побудуємо пряму, при=1:

Геометричний зміст задачі лінійного програмування полягає в тому, щоб серед паралельних прямих , які мають спільну точку з множиною значень знайти найменш (або найбільш) віддалену від початку координат.

З малюнку видно, що при наша функція набуває найменшого значення.

Мінімальне значення функції дорівнює 1.6, воно досягається в точці x=6, y=1.

Зазначимо, що коли в цій задачі знаходити не мінімум, а максимум функції, то задача не матиме оптимального розв’язку, бо многокутник розв’язків системи не обмежений зверху.

Завдання для самостійної роботи

Знайдіть мінімум функції при зазначених обмеженнях графічно та за допомогою блокуGiven:

№		обмеження
	x+2y
	4x-2y
	x-y
	2x-5y
	3x+y
	3x+5y
	4x+5y

Додаток

Розв’язування систем нерівностей

Графічно розв’язати систему нерівностей

Для того, щоб розв’язати систему нерівностей накреслимо всі обмежуючи лінії і отримаємо многокутник розв’язків системи.

Для більш наочного представлення зафарбуємо многокутник розв’язків системи. Будемо перевіряти точки, з наперед заданого проміжку, чи попадають вони в многокутник, і якщо так, то наносити їх на малюнок.

Задамо кількість точок, які будуть заповнювати многокутник:

_{Обмежимо пошук точок прямокутною областю:}

Задамо функцію Test, яка перевіряє належність точок до многокутника:

Блок програми, який шукає N точок, що належать многокутнику:

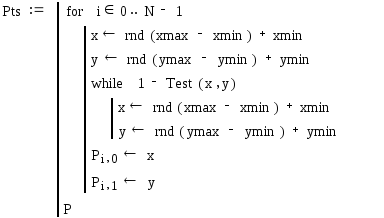
Координати Х,Y які належать області: Графік

Лабораторна робота № 34

Тема: Функції для розв'язування диференційних рівнянь.

Мета: Навчитися розв'язувати диференційні рівняння засобами Mathcad.

Теоретичні відомості

Mathcad дозволяє розв'язувати диференційні рівняння, а також системи диференційних рівнянь чисельними способами. В окремих випадках, можна отримати і аналітичний розв'язок диференційних рівнянь.

Чисельне розв'язування диференційних рівняння

Для чисельного розв'язування рівняння існує декілька функцій. Питання про використання тієї чи іншої функції залежить від відомостей про характер поведінки диференційної функції. Перелік функції можна отримати зі справочної системи Mathcad.

Z:=rkfixed(y,x1,x2,n,D) – обчислює таблицю значень з (m+1) стовпцями і n рядками (m-число рівнянь у системі). Нульовий стовпець таблиці – це поточні значення незалежної змінної х. Вони визначаються через х1, х2 і n. Наступні стовпці розв'язку визначають значення шуканих функцій у1(х), у2(х), ... для відповідних поточних значень аргументу;

у – вектор початкових наближень;

х1, х2 – інтервал інтегрування;

n – кількість кроків;

D – вектор похідних (рівняння, представлені у прийнятній для Mathcad формі).

Z:=Rkadаpt(y,x1,x2,n,D) – обчислює таблицю значень розв'язку методом Рунге-Кутта зі змінним кроком, початкові умови задані у векторі у, інтервал х1..х2, n- кількість кроків, D – праві частини рівняння.

Z3:=Bulstoer(y,x1,x2,n,D) – обчислює таблицю значень розв'язку методом Булирша-Штера, більш точніше, ніж методом Рунге-Кутта застосовується, якщо заздалегідь відомо, про гладкий вигляд функції.

Приклад 1. Розв'язати задачу Коші для рівняння першого порядку:

,

• Задайте початкову умову (матрицю у):

• Введіть матрицю похідних. Вона складається з одного елемента і співпадає з правою частиною рівняння:

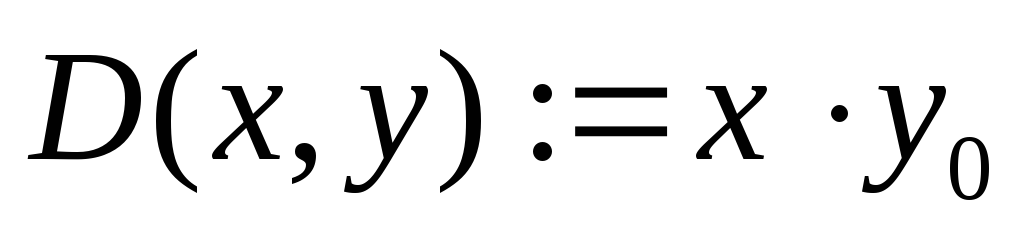
• Задайте інтервали інтегрування х1:=0 х2:=1

• Розв'язуємо диференційне рівняння:

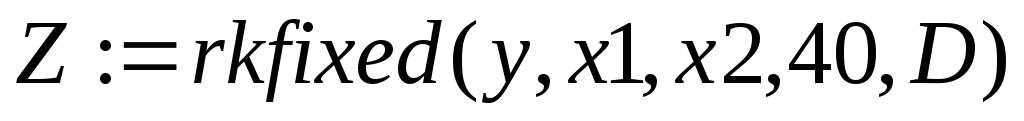
Отримали матрицю Z. Перший стовпчик містить точки, в яких отримали розв'язок, а другий стовпчик – самі розв'язки.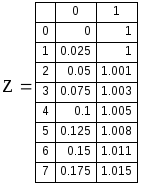

• Побудуйте графік

Приклад 2. Розв'язати задачу Коші для рівняння другого порядку: , у(0)=0, у'(0)=1.

Підготовчий етап:

• Перед розв'язуванням диференційного рівняння його треба представити у вигляді системи рівнянь першого порядку методом заміни.

диф рів. містить 2-у похідну, яку представимо як похідну від першої

Проведемо заміни: у0=у(х) і підставимо в вихідне рівняння

Отримаємо систему двох рівнянь першого порядку:

_{вектор правої частини системи}

інтервал інтегрування

кількість кроків

вектор початкових наближень результат розв'язку у вигляді таблиці

Розв'язування диференційних рівнянь за допомогою блоку Given

• Введіть слово Given

• Задайте диференціальне рівняння і його обмеження, використовуючи логічні оператори = (ctrl+=)

• Введіть функцію odesolve(х,b,[step]), де х – змінна, b – кінцева точка.

За замовчуванням функція використовує метод Рунге-Кутта з фіксованим кроком. Щоб застосувати адаптивний метод, виберіть з контекстного меню функції odesolve пункт Adaptive.

Обмеження можуть бути задані в будь-якому порядку, але диференціальному рівнянню n-го порядку повинні відповідати n незалежні початкові умови. Умови типу нерівностей не дозволяються.

Приклад 3. Розв'язати рівняння

Given

_{// для введення ' використовують ctrl+F7 чи клавішу біля 1}

Аналітичне розв'язування диференціальних рівнянь

Mathcad прямо не розв'язує диференційні рівняння в аналітичному вигляді, але можна скористатися прямим і зворотнім перетворенням Лапласа.

Перетворення Лапласа дозволяє переходити від рівнянь з комплексними величинами до рівнянь з дійсними величинами, диференціювання заміняти множенням.

Пряме перетворення Лапласа трансформує диференціальне рівняння у відповідне алгебраїчне, котре може бути потім розв'язано аналітичним способом. Зворотне перетворення перетворює аналітичний розв'язок алгебраїчного рівняння в аналогічний розв'язок диференціального рівняння з урахуванням початкових умов.

Приклад 4. Розв'язати рівняння

1. Введення диф.рівняння і проведення прямого перетворення Лапласа:

• Введіть вихідне рівняння і виділити в ньому кутком змінну t

• Виконайте команду головного меню Symbolics(Символи)  Transform (Перетворення)  Laplase (Лапласа). З'явиться результат перетворення:

• Виконайте заміну: замість laplase(x(t),t,s підставити z, а замість d/dt х(0) – С1

• Виділіть змінну z і розв'язати вираз за допомогою меню Symbolics (Символи)  Змінні  Обчислити

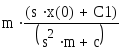
2. Зворотне перетворення Лапласа по змінній s:

• Виділіть кутом змінну s в отриманому розв'язку

• Виконайте команду головного меню: Symbolics (Символи)  Transform (Перетворення)  Inverse Laplase (Лапласа Обернене). З'явиться результат перетворення. Якщо вийде, то спростіть вираз.