
- •Т. А. Сливина математическая логика и теория алгоритмов
- •Глава I. Логика высказываний 6
- •Глава 1 логика высказываний
- •§ 1. Логические операции над высказываниями
- •§ 2. Формулы логики высказываний. Основные равносильности и преобразования
- •1. Основные равносильности
- •2. Равносильности, выражающие одни логические операции через другие
- •3. Равносильности, выражающие основные законы алгебры логики
- •§ 3. Алгебра Буля. Функции Буля. Представление произвольной функции алгебры логики в виде формулы алгебры логики
- •§ 4. Дизьюнктивная нормальная форма и совершенная дизьюнктивная нормальная форма. Коньюнктивная нормальная форма и совершенная коньюнктивная нормальная форма
- •§ 5. Приложения алгебры логики в технике и других областях
- •Задачи и упражнения
- •Глава 2 исчиление высказываний
- •§ 1. Этапы построения исчисления высказываний. Понятие формулы исчисления высказываний
- •§ 2. Определение доказуемой формулы. Правила вывода и заключения
- •§ 3. Производные правила вывода
- •§ 4. Выводимость формул из совокупности формул
- •§5. Доказательство некоторых законов логики
- •3. Закон разъединения посылок
- •5. Закон исключенного третьего: ├
- •§6. Связь между алгеброй высказываний и исчислением высказываний
- •§7. Проблемы аксиоматического исчисления высказываний
- •1. Проблема разрешимости исчисления высказываний.
- •3. Проблема полноты исчисления высказываний.
- •4. Проблема независимости аксиом исчисления высказываний.
- •Задачи и упражнения
- •Глава 3 логика предикатов
- •§ 1. Понятие предиката. Логические операции над предикатами. Кванторные операции.
- •§ 2. Понятие формулы логики предикатов. Значение формулы логики предикатов
- •§ 3. Равносильные формулы логики предикатов. Предваренная нормальная форма
- •§ 4. Общезначимость и выполнимость формул. Проблема разрешимости для общезначимости и выполнимости, неразрешимость ее в общем случае
- •§ 5. Применение языка логики предикатов для записи математических предложений, определений, построения отрицания предложений
- •§ 6. Замечание об аксиоматическом исчислении предикатов
- •Задачи и упражнения
- •Глава 4 математические теории
- •§ 1. Теории первого порядка. Основные понятия
- •§ 2. Примеры математических теорий из алгебры, анализа, геометрии
- •1. Теория частичного упорядочения.
- •2. Теория групп.
- •3. Аффинная геометрия.
- •§ 3. Интерпретация языка теории
- •§ 4. Проблемы непротиворечивости, полноты, разрешимости теории
- •2. Проблема полноты.
- •3. Проблема разрешимости.
- •Глава 5 алгоритмы
- •§ 1. Понятие алгоритма и его характерные черты
- •§ 2. Разрешимые и перечислимые множества
- •§ 3. Уточнение понятия алгоритма
- •§ 4. Вычислимые функции. Частично рекурсивные и общерекурсивные функции
- •1. Суперпозиция функций.
- •2. Схема примитивной рекурсии.
- •§ 5. Машины Тьюринга
- •§ 6. Нормальные алгоритмы Маркова
- •§ 7. Неразрешимые алгоритмические проблемы (обзор)
- •1.Неразрешимость проблемы распознавания выводимости в математической логике.
- •3. Проблема эквивалентности слов для ассоциативных исчислений.
- •4. Неразрешимость десятой проблемы Гильберта о диофантовых уравнениях.
- •Задачи и упражнения
- •Заключение
- •Библиографический список
- •Математическая логика и теория алгоритмов
- •660014, Красноярск, просп. Им. Газ. «Красноярский рабочий», 31.
- •660028, Г. Красноярск, ул. Водопьянова, 2-241.
§ 5. Приложения алгебры логики в технике и других областях
Среди технических средств автоматизации значительное место занимают устройства релейно-контактного действия, переключательные схемы. Они широко используются в технике автоматического управления, в электронно-вычислительной технике и т. д. Такие устройства называют релейно-контактными схемами (РКС). В силу того, что они содержат большое количество реле, электронных ламп, полупроводников и электромагнитных элементов, описание и конструирование их весьма затруднительно.
Использование алгебры логики в конструировании РКС оказалось возможным в связи с тем, что каждой схеме можно поставить в соответствие некоторую формулу алгебры логики, и каждая формула алгебры логики реализуется с помощью некоторой схемы. Это обстоятельство позволяет выявить возможности заданной схемы, изучая соответствующую формулу, а упрощение схемы свести к упрощению формулы. С другой стороны, до построения схемы можно заранее описать с помощью формулы те функции, которая схема должна выполнять. Впервые на это указал в 1910 году физик П.С. Эренфест.
Рассмотрим, как устанавливается связь между формулами алгебры логики и переключательными схемами.
Под переключательной схемой будем понимать схематическое изображение некоторого устройства, состоящего из следующих элементов:
1) переключателей, которыми могут быть механические действующие устройства (выключатели, переключающие ключи, кнопочные устройства и т.д.), электромагнитные реле, электронные лампы, полупроводниковые элементы т.п.;
2) соединяющих их проводников;
3) входов в схему и выходов из нее (клемм, на которые подается электрическое напряжение). Они называются полюсами схемы.
Сопротивления, конденсаторы и т. д. на схемах не изображаются.
Переключательной схемой принимаются во внимание только два состояния каждого переключателя, которые называют «замкнутым» и «разомкнутым».
Рассмотрим
простейшую схему, содержащую один
переключатель Р.
Переключателю Р
поставим в соответствие высказывание
р
– «переключатель Р
замкнут», а переключателю ![]() поставим в соответствие высказывание
поставим в соответствие высказывание
![]() – «переключатель Р
разомкнут». Если принять во внимание
не смысл высказывания, а только его
значение, то можно считать, что любому
высказыванию может быть поставлена в
соответствие переключательная схема
1.
– «переключатель Р
разомкнут». Если принять во внимание
не смысл высказывания, а только его
значение, то можно считать, что любому
высказыванию может быть поставлена в
соответствие переключательная схема
1.

Схема 1
Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы.
Коньюнкция двух высказываний p и q будет представлена схемой с последовательным соединением двух переключателей P и Q (схема 2).
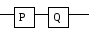
Схема 2.
Эта
схема пропускает ток тогда и только
тогда, когда истинны оба высказывания
p
и q,
то есть истинна коньюнкция ![]() .
.
Дизьюнкция двух высказываний p и q будет представлена схемой с параллельным соединением двух переключателей P и Q (схема 3).

Схема 3.
Эта
схема пропускает ток тогда и только
тогда, когда истинно хотя бы одно из
высказываний p
или q,
то есть истинна дизьюнкция ![]() .
.
Из схем 1, 2 и 3 путем последовательного и параллельного соединения могут быть построены новые переключательные схемы.
Учитывая, что любую формулу алгебры логики с помощью равносильных преобразований можно представить в виде формулы, содержащей только операции дизьюнкция, коньюнкция и отрицание, то любую формулу можно представить в виде схемы, и обратно, любую схему можно записать в виде соответствующей формулы.
Упрощение исходной схемы производится по следующему алгоритму:
записать схему в виде формулы
упростить формулу, используя основные тождества
по упрощенной формуле начертить схему
Пример:
Для заданной схемы

записать формулу и упростив ее, построить более простую схему.
Формула, соответствующая данной схеме:
A&
(((![]() vBvC)&
vBvC)&![]() )v(((
)v(((![]() &
&![]() )v(B&
)v(B&![]() ))&
))&![]() )v(A&
C))
)v(A&
C))
Упростим формулу с помощью основных тождеств:
Рассмотрим первую (верхнюю) ветвь схемы: (
 vBvC)
&
vBvC)
& = (
= ( vBvC)
&C=(
vBvC)
&C=( &
& )v(B&
)v(B& )v(C&
)v(C& )
= (
)
= ( 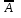 &
& )v
(B&
)v
(B& )v
0=(
)v
0=( &
& )v(B&
)v(B& )
)Рассмотрим вторую (среднюю) ветвь схемы:
(![]() &
&![]() )v(B&
)v(B&![]() ))&
))&![]() = (
= (![]() &
&![]() )v(B&
)v(B&![]() ))&
))&![]() =
=![]() &
&![]()
Тогда результирующая формула примет вид:
A&
((![]() &
&![]() )v(B&
)v(B&![]() )v
(
)v
(![]() &
&![]() )v
(A&C)) = A((B&
)v
(A&C)) = A((B&![]() )v(
)v(![]() &
&![]() )v(A&C))
= (B&
)v(A&C))
= (B&![]() &A)v
(
&A)v
(![]() &
&![]() &A)v
(A&C&A)=((A&
&A)v
(A&C&A)=((A&![]() )&B)v(A&C)
= ((A&
)&B)v(A&C)
= ((A&![]() )v(A&C))
& ((A&C)vB) = A& ((A&C)vB) =
(A&A&C)v(A&B)=(A&C)v(A&B)=A& (BvC)
)v(A&C))
& ((A&C)vB) = A& ((A&C)vB) =
(A&A&C)v(A&B)=(A&C)v(A&B)=A& (BvC)
Таким образом, исходная схема приняла следующий вид:

Из рассмотренного примера следует, что для некоторых РКС путем равносильных преобразований соответствующей формулы алгебры логики можно получить РКС, содержащую меньшее число переключателей. Проблема решения этой задачи носит название проблемы минимизации.
Основными функциональными компонентами цифровых компьютеров являются электронные (комбинационные схемы). Будем рассматривать электронные компоненты, собранные в цепь, которая имеет несколько входов и один выход (логические ворота). Такую схему также можно записать в виде булевой функции, изображая и обозначая компоненты таким образом:
( отрицание)
отрицание)
(конъюнкция)
v (дизъюнкция)
Так же определены следующие логические вентили:

f=(![]() )=
)=![]() И-НЕ
И-НЕ
f=(![]() )=
)=![]() ИЛИ-НЕ
ИЛИ-НЕ
f=(![]() )=
)=![]() ИСКЛЮЧАЮЩЕЕ ИЛИ
ИСКЛЮЧАЮЩЕЕ ИЛИ
Упрощение исходной схемы производится по следующему алгоритму:
записать схему в виде формулы
упростить формулу, используя основные тождества
по упрощенной формуле начертить схему
Пример:

Формула,
соответствующая данной схеме: F=(![]() )&y&(xvz)
)&y&(xvz)
Упростим формулу с помощью основных тождеств:
согласно закону поглощения (
 )&y=у
)&y=уF=y&(xvz).
Применение методов алгебры логики не замыкается только на применение в технике, они широко используются и при решении логических задач. Суть применения методов алгебры логики к решению логических задач состоит в том, что, имея конкретные условия логической задачи, необходимо записать ее в виде формулы алгебры логики. Затем путем равносильных преобразований упрощают полученную формулу. Простейший вид формулы, как правило, приводит к ответу на все вопросы логической задачи.
Приведем пример, использования возможностей алгебры логики для решения элементарных логических задач.
Пример:
Пытаясь вспомнить победителей прошлогоднего турнира, пять бывших зрителей турнира, заявили:
1. Антон был вторым, а Борис – пятым.
2. Виктор был вторым, а Денис – третьим.
3. Григорий был первым, а Борис – третьим.
4. Антон был третьим, а Евгений – шестым.
5. Виктор был третьим, а Евгений – четвертым.
Впоследствии выяснилось, что каждый зритель ошибся в одном из двух своих высказываний. Каково было истинное распределение мест в турнире?
Решение:
Обозначим высказывания зрителей символом
![]() ,
где Х
– первая буква имени участника турнира,
а у
– номер места, которое он занял в турнире.
Согласно условию задачи дизьюнкции
высказываний будут истинны
,
где Х
– первая буква имени участника турнира,
а у
– номер места, которое он занял в турнире.
Согласно условию задачи дизьюнкции
высказываний будут истинны
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Тогда будет истинной и формула
![]() (
(![]() )(
)(![]() )(
)(![]() )(
)(![]() )(
)(![]() ).
).
Путем равносильных преобразований получим
![]()
![]()
![]()
![]()
![]()
![]() .
Но, так как
.
Но, так как ![]() ,
значит,
,
значит,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
что и дает ответ на вопрос задачи.
,
что и дает ответ на вопрос задачи.
